作図の話題二つ

＜三平方の定理の始まり＞
古代バビロニア王国（紀元前１８３０～紀元前１５３０）の時代の粘土板には、すでに「三平方の定理」に関する記述が残されているという。
その後、ピタゴラスが発見したという逸話が生まれ、ヨーロッパでは「ピタゴラスの定理」と呼ばれるようになる。
また、古代中国では「鈎股弦の定理」と呼ばれ、日本にも伝えられる。

＜和算の中心から規矩術へ＞
そして、日本では江戸時代に「和算」の中心となる定理として活用・発展する。
その実用的な発展の一つが、木造大工の技術である「規矩術」である。「規」はコンパスで、「矩」は定規を意味する。

　江戸幕府の大棟梁：平内延臣（１７９１～１８５６）によって大成したという。曲尺ひとつで巧みに墨付けし、材料を加工し組み立てる技術である。

＜作図問題との関連＞
「規」がコンパスで、「矩」が定規だとすると、古代ギリシャ時代の作図問題を思い出す。
例えば、コンパスと定規だけで、「任意の角を三等分する方法」を示せ、という問題などである。
違いは、「矩」の定規には目盛りがあり、古代ギリシャ時代の問題では「目盛り無しの定規」を用いることである。
目盛りのある「矩」を用いた「規矩術」では「立方根」まで作図によって求めていたという。（したがって、体積が２倍のマスを作図する古代ギリシャ時代の難問にも答えられたことになる。）

＜中勾の長さ＞
さて、規矩術では「鈎股弦」の文字は「勾殳玄」と簡略されて用いられている。そして、屋根の造築において用いられる「平勾配」を示す次図にその典型が見られる。

＜平勾配に関わる図＞

殳の長さを「一尺」として、それに対する勾の長さで「平勾配」が示される。「一寸勾配」、「二寸勾配」、「三寸勾配」、・・・のように用いられる。
勾の長さが変われば、玄の長さも、その他（欠勾、小殳など）の長さも変わる。
それで、仕事の効率を上げるために「一覧表」が作られている。

＜規矩術の一つ＞
ところで、直角三角形の直角の頂点（Ｂ）から玄に下ろした垂線「ＢＤ」を「中勾」と呼ぶ。中勾は玄を「長玄」と「短玄」に分割する。
　　　　　中勾＝　√（長玄）×（短玄）
この時、「中勾」の長さは上式となることが「規矩術」に示されている。
この式で「短玄＝１」とすると、長玄がどんな数であっても、中勾は長玄にルートを付けた数になる。
例えば、長玄が「1+√2」だとすると、中勾は次のようになる。

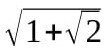
この値は、方程式「x＾4−2x＾2−1＝0」の一つの解である。この方程式は
二次方程式を組み合わせることで解くことができる。したがって、この値は作図可能であることが分かる。
この値の作図方法の一つを次図に示しておく。

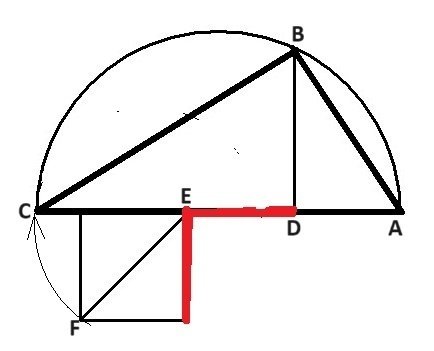
ＡＢが勾で、Ｂからの垂線（BD）が中勾である。
ＡＤは短玄となり、これを「１」とする。
長玄は「ＤＥ＋ＥＣ」でＥＣは正方形の対角線ＥＦと等しい。
それで、長玄は「1+√2」となる。
ＡＣを直径とする半円にＤからの垂線を引き、その交点をＢとすると、ＢＤが求める長さとなる。

＜モーリーの定理へ＞
作図に関するもう一つの話題は、「角の三等分」の問題から生まれた美しい定理である。

三角形は最も単純な平面図形である。三つの頂点、三つの辺、三つの内角によって構成される。
それで、「ユークリッド原論」には三角形にひそむ性質について種々述べられている。特に、第四巻には三角形の内接円や外接円についての記述がある。

＜内心、外心、重心、・・・＞
古代ギリシャ数学において、任意の角の二等分の作図や、線分の垂直二等分線の作図は基本であり、それを活用して「内心」や「外心」の存在が示されている。

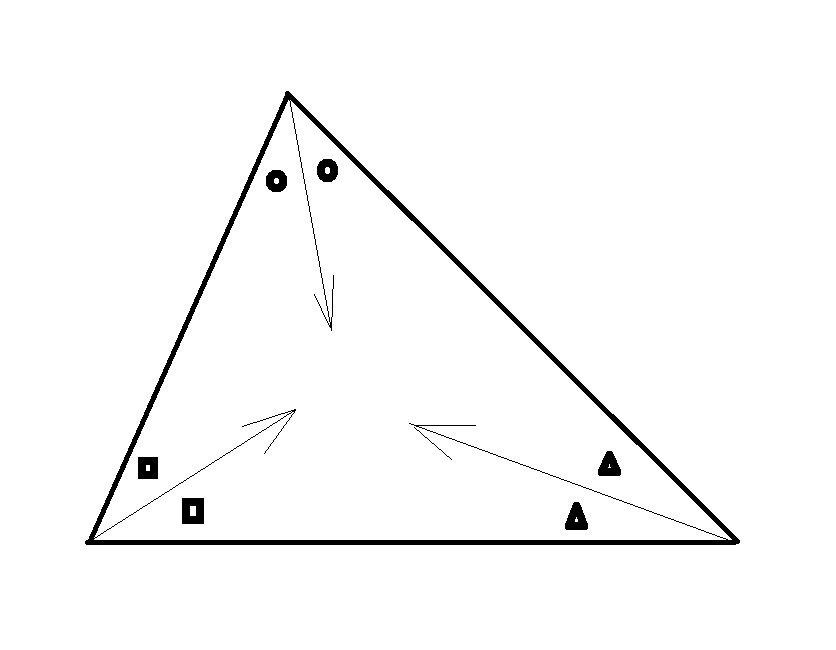
三角形の三つの内角の二等分線は三本である。その三本の直線が「一点で交わる」という事実は、奇跡的にも見える。

しかし、決して奇跡などではないことを「証明」し、全ての三角形にひそむ性質として、「内心」が存在するという事実を示すことができる。

　同様な意味で、全ての三角形にひそむ性質として、「外心」が存在する。
それぞれの辺の垂線が一点で交わるのである。

また、三辺のそれぞれの中点から向かい合う頂点への直線もまた三本あり、その三本が一点で交わる。これも二千年以上前から知られている「重心」である。

重心は均一な材料の三角形であれば、その一点で支えることができるという分かり易い性質をもっている。
しかも、作図は簡単である。

他は省略するが、鈍角をもたない三角形であれば、その内部に「内心」、「外心」、「重心」、「垂心」の四点（四心）が存在することが知られている。
高校の数学では「傍心」を加えて「五心」と呼ぶ場合もある。

　さて、三角形の内部にひそむものとして「五心」があることは古代ギリシャ時代から知られていたことである。
そして、最も基本的な平面図形である「三角形について人類は調べ尽くした」と思われていた。
しかし、盲点があった。それは、「任意の角の三等分の作図は不可能である」という事実によってさえぎられていたのである。

＜角の三等分問題＞
　任意の角を三等分する作図方法は古代ギリシャから続く問題であった。
これが「不可能である！」という決着がつくのは１８３７年のことである。
それまで、「角の三等分問題」は作図が「可能か不可能か」に焦点が絞られていた。
そして、ピエール・ヴァンツェルが（例えば６０度を３等分するためには）三次方程式「x＾3−3x−1=0」の解は平方根（ルート）だけでは表せないことを示し、「作図は不可能である」ことを証明した。
　　　　　　　　　　　　　　＜3倍角の公式＞
　　　　　　　　　　　　cos3α=4（cosα）＾３−3cosα
　　　　　　　　　　　　　　いま3α=60度とする。
　　　　　　　　　　　　cos60=4（cos20）＾３－3cos20
　　　　　　　　　　　　　　両辺を２倍すると
　　　　　　　　　　　　２(1/2)=8（cos20）＾３－6cos20
　　　　　　　　　　　　　　2cos20＝x とすると
　　　　　　　　　　　　　　　１　＝　x＾3 –　３x

さらに一般的な理論として、ガロア（１８１１～１９３２）によるガロア理論が新しい地平が拓くのを待っていた。

エバリスト・ガロアが決闘で倒れた後の１８４６年に、リュウビルが数学雑誌にガロアの論文を発表する。すると、デーデキントをはじめとして高名な数学者が注目し、ガロア理論が世に出ることになる。
「角の三等分問題」の機は熟していたのである。

＜モーリーの定理発見＞
任意の角の三等分について、「定規とコンパスのみ」の作図は不可能であることが明らかになった。しかし、「定規とコンパスのみ」という条件を外せば当然であるが三等分はできる。
二等分、三等分、四等分、・・・の間には壁はなくなったのである。
そんな雰囲気の時代になり、イギリス生まれのアメリカ人数学者フランク・モーリー（１８６０～１９３７）は１８９９年に「モーリーの定理」を発見する。

それは、三つの内角の二等分線の交点が内心であることを踏まえたもので、「二等分」を「三等分」に変えた所に見えたものである。
すなわち、三つの内角のそれぞれを三等分する直線を引き、その交点を結ぶと「正三角形」になる、というものである。これは、全ての三角形には「正三角形」がひそんでいることを意味している。

＜すべての三角形に正三角形がひそんでいる＞
この定理が発表されると、モーリー自身を含めた世界中の数学者が「何故これまで発見されなかったのか不思議だ」と話したという。

　これまで、「内心」、「外心」、「重心」、「垂心」の存在証明には触れていない。「モーリーの定理」についても、ここでは触れないことにする。

＜外心、重心、垂心が一直線上に＞
　そして、これまでの一般の三角形についての調査から、「直角三角形」の場合について整理してみることにする。
次のような「3:4:5」の直角三角形の場合について整理してみる。（座標軸上の図形として見ることにする。）

まず、垂心、重心、外心は同一直線上にある。（この直線の式は「y=(3/4)x」である。）

垂心の座標は（0,0）であり、外心の座標は（2, 1.5）である。
重心の座標は「y=(-3/2)x+3」と「y=(3/4)x」との交点として求めると（4/3, 1）である。

そして、内心の座標は（1,1）である。これは「y=x」の直線と「y=−2x+3」の交点として求められる。
これらの座標から、内心、外心、重心、垂心の定義に合致しているかどうか確認してみるとよい。

同様に、モーリーの定理についても、三つの交点の座標を求めて「正三角形」であることを確認して欲しい。