連分数を使って不定方程式を解く

　センター試験から共通テストになり出題の傾向が変化しました。センター試験のときよりも数学的な背景がある問題を出そうとしているように思います。もちろん，まだ第 1 回の共通テストは実施されていませんので，共通テスト向けの問題集を解いた感想です。

　さて，そんな共通テスト向けの問題を解説していると連分数で不定方程式を解くという問題に出会いました。
　そもそも連分数とは何なのか。なぜ不定方程式を解けたのかを解説したと思います。

1．連分数とは

　連分数とは，分母に更に分数が含まれているような分数のことである。特に分子がすべて 1 である場合を単純連分数という。

　例えば，次のような分数のことです。

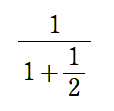
　　もっと長くなっても大丈夫です。

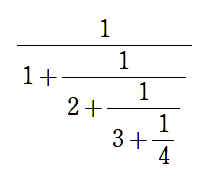
　このような形で分数の中に分数がつながったものを連分数といいます。

2．連分数で約分をする

　分母分子ともに大きな数であり，約分が簡単にできないときに連分数が役に立ちます。

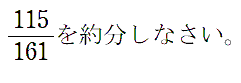
　たとえばこの問題を解いてみましょう。普通にしても約分はできますが連分数を使って解いてみます。
　まず，この分数を連分数展開します。

　最後に出てきた連分数を逆の手順で戻していくと

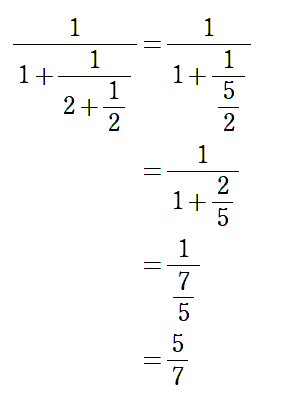
となります。
　115 = 23×5，161 = 23×7 ですので普通に約分しても同じ結果になります。
　この連分数を使った約分は，中学入試において有名なテクニックです。

　勘のいい人は気がついたかもしれませんが，連分数に展開するということはまさしくユークリッドの互除法をしていることに他なりません。

　ユークリッドの互除法に他ならないということは，連分数を使って不定方程式を解けるのでは！？　という期待が持てます。

3．連分数で二元一次不定方程式を解く

　共通テストの問題集で連分数を使って二元一次不定方程式を解く方法が，太郎さんと花子さんによって紹介されていました。

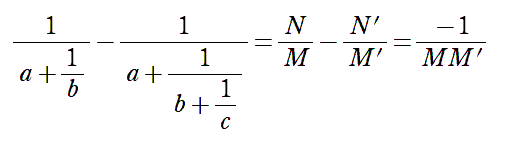
　普通の分数にして通分した結果，分子が －1 になることが文字式の計算でわかります。

　さらに，連分数を長くしても似たようなことが起きます。

　今度は分子が 1 になりました。

　この性質は更に長い連分数でも成立するようです。
　理解を深めるために具体例を計算してみましょう。

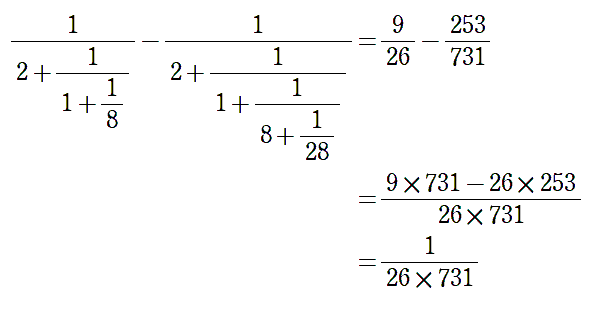
　最後の 9×731 - 26×253＝1 は性質から計算することなく求まります。
　つまり，次のような二元一次不定方程式を解くことができます。

　この問題に対する解答は，上の計算から x=9 , y=26 と求まります。

　この問題をユークリッドの互除法を使って解いてみましょう。
　そして，連分数での計算と互除法での計算を見比べることで上のような性質が成り立つことを実感してみたいと思います。

　まず，731 と 253 でユークリッドの互除法を使います。

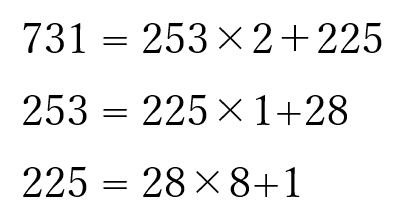
　商の部分が連分数に登場していることに注目してください。

　次にここから標準的な（？）方法で不定方程式の解のひとつを見つけます。

　では，解となる 26 と 9 での互除法も並べて，商を区別してみましょう。

　数式がけたたましくて申し訳ないのですが，このように並べてみると理解ができます。

(ア) 連分数に登場する数字は互除法での商になる。
(イ) 1 つ手前の連分数で作られた数字の組（26と9）の互除法での商は元の組（731と253）の互除法の商と一致している。
(ウ) 互除法を逆戻りすることで不定方程式の解を得られる。
よって，連分数を使って不定方程式が解ける。

　高校数学ではあまり目にしない連分数ですが，連分数だけで 1 冊本が書けるほど奥の深い性質を持っています。
　興味がありましたらぜひ調べてみてください。