
「Kaggleで勝つデータ分析の技術」2章 QWK についての補足
私事ですが,先日開催されていました「Kaggleで勝つデータ分析の技術」(以下,Kaggle 本)の勉強会にひっそりと参加してきました.
私が執筆担当をしていました 2 章をちょうどやるとのことで,読者の方々はどんなところで詰まるか,もしくは分かりにくいと感じるかを勉強させていただくのに良い機会と考えたのが参加理由でした.
勉強会中に,「2.3.5 多クラス分類における評価指標」の中の Quadratic Weighted Kappa(以下,QWK)に関して,発表担当の方が疑問点を述べられていましたので,今日はその点に関して簡単な補足をしたいと思います.
1. はじめに
QWK はマルチクラス分類用の評価指標で,クラス間に順序関係があるような場合に使用されます.
2019年の 6 月末から 9 月初頭にかけて Kaggle で開催された APTOS 2019 Blindness Detection でもこの指標が使われていました.このコンペでは,参加者は対象者の網膜画像をもとに,糖尿病性網膜症のリスクの大きさを分類することが求められていました.所謂,画像分類タスクですね.
下図は 0 から 4 へと数字が大きくなるにつれ増す重症度とそれに対応した網膜画像を示したものです.(DR = Diabetic Retinopathy,糖尿病性網膜症)

この場合,クラスを 0 から 4 の数字で表現することになりますが,0 から 4 の数字は互いに無関係ではなく,0 と判断されたクラスよりは 1 と判断されたクラスの方が糖尿病性網膜症のリスクは高くなります.同様に,1 よりも 2 の方が,2 よりも 3 の方が・・・と,同じことがいえます.
余談ですが,このコンペは私も参加していましたので,もしご興味のある方は私の Speaker Deck をご覧いただくとコンペの雰囲気が分かるかもしれません.
https://speakerdeck.com/hoxomaxwell/aptos-2019-28th-place-solution
2. QWK を構成する 3 つの要素(O_ij, w_ij, E_ij)について
話が少し逸れてしまいましたので,話題を元に戻します.クラス間に順序関係がある場合の例として,Kaggle のコンペにちなんだ形で上記例を挙げましたが,この記事では簡単のため以下のような 3 つのクラスからなる例を扱いたいと思います(Kaggle 本の例と合わせてあります).

ここで挙げている例の場合,データ点数は 100 あり,Actual とあるのが正解に対応し,Predicted とあるのが予測に対応する軸となります.クラスは 1 から 3 の 3 種類ですので,3 x 3 = 9 個分のセル内に,対応するデータの点数が記入された形となっています.この 3 x 3 のセルは混同行列(Confusion Matrix)と呼ばれます.仮に 100 % の正答率をもつモデルを作成できたのであれば,対角成分以外には全て 0 の値が入ることになります.
そして,QWK の計算式は Kaggle 本にもあります通り以下となります.(どうでもいいことですが,note は数式を tex 形式で直接入力できないのが少し厳しいですね.どなたか良い対処法をご存知でしたら教えてくださると助かります.)
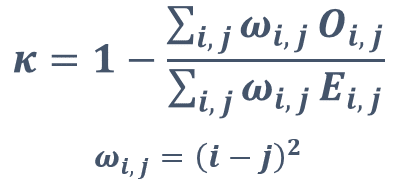
O_ij (O: Observe)は正解のクラスが i で予測のクラスが j のレコード数を表します.例えば,先ほどの混同行列の図の場合,O_11 = 10,O_13 = 15 となります.
w_ij は,クラスの予測を外した場合に対するペナルティを表します.今の場合ですと,クラスは 1 から 3 までの 3 種類ですから,対応するペナルティは下図のようになります.

一方で,E_ij (E: Expectation)は, Kaggle 本では「正解のクラスと予測のクラスの分布が互いに独立であるとした場合に,各セル(i, j)に属するレコード数の期待値で,正解のクラスが i である割合 × 予測のクラスが j である割合 × データ全体のレコード数として計算される」としました.
ここの記述が読者の方によっては分かりにくいとのことですので,この記事ではここをもう少し簡単に説明したいと思います.
E_ij に対応するレコード数は下図の通りです.
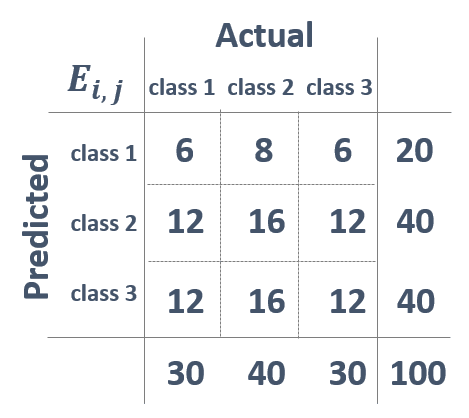
例えば,E_11 の場合,20/100 × 30/100 × 100 = 6 となります.
これを 9 セル分計算することになるわけですが,一体これは何を意味しているのでしょうか?
簡単にいってしまうと,E_ij は「正解・予測の各クラスの割合を固定したままランダムに予測すると,どれだけのレコード数が割り当てられるかを計算したもの」になります.
少し具体的にみてみましょう.
例えば,先ほどの E_11 の場合ですと,
正解のクラスが 1 である割合は 30%
予測のクラスが 1 である割合は 20%
となっています(2022/08/09 に Kinako さんにご指摘いただき修正).
正解と予測のクラスがどちらも 1 となる確率は,正解と予測の分布がそれぞれ独立である考えた場合,20% × 30% = 6% となります.全レコード数である 100 を掛けてあげることで,6% × 100 = 6 とE_11 に該当するレコード数を求めることができます.
後は,この計算を全 9 セル分行うことでランダムに予測した場合の混同行列 E_ij を得ることができます.
ここでいう「ランダム」というのは,正解と予測の分布だけは反映した形で,あてずっぽうに各レコードにクラスを割り振ることを意味します.
3. QWK は何を計算しているか?
O_ij,E_ij,w_ij の意味しているところはなんとなくお分かりいただけたのではないかと思います.せっかくですので,最後に QWK への理解を少し掘り下げてみましょう.QWK の数式で重要なのは,数式中の以下の部分です.
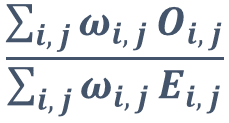
分子はモデルの予測と正解にもとづいて計算される値ですが,分母は予測と正解のクラス分布を前提にしたあてずっぽうモデルにより求まる値です.
その 2 つの比をとっているわけですから,作成したモデルがどれだけあてずっぽうモデルに対して良い予測ができているかを計算している,と定性的に理解できそうです.そして,あてずっぽうになればなるほど,O_ij は E_ij に近づき,上の式は 1 に近づきますから結果的に QWK は 0 になります.
さて,ここまで読んでくださった読者の方々はお気づきかと思いますが,この指標の面白いところは分母の E_ij の計算の際に予測のクラス分布を使用しているところです.
少し簡単な実験をしてみましょう.
そのために下図のような状況を考えます(前述の分布とは少し異なります).

図中の X は 0 <= X <=70 を満たす整数で,この値によって予測の分布(クラス 1 と 2 の分布)が変わります.X の値が決まれば,E_ij 内の 9 つのセルの値は自ずと決まります.一方で,O_ij の方は 4 つのブランクセル(図中の灰色部分)がありますが,制約式を考慮すると自由度はたった 1 つしかありません.この場合,QWK を最大化させるような値の配置を計算するのは,X が整数であっても難しいことではありません(制約式は 4 つあるようにみえますが,実質の制約式による自由度の削減数は 3 です.独立性の検定を行うカイ二乗検定の自由度の求め方などを思い出すと良いかもしれません).
各 X の値に対して実現可能な QWK の値をプロットしたものがこちらです.

ご覧いただくと分かる通り,X = 30 つまり正解と予測のクラス分布が等しい時に,実現可能な QWK の最大値は 1.0 となります.
一方で,X = 30 以外の値ですと,どんなに良い予測をしても,実現可能な QWK の最大値は 1.0 にはならないことが分かります.
このように, QWK という指標は予測したいデータのクラス分布を意識した形でモデルの作成を行う必要があることが分かります.QWK が採用されたコンペに参加する際は,この点に気をつけておくと良いと思います.
補足1
Kaggle において QWK が評価指標になっていた場合,気をつけなければならないのは,public と private のクラス分布が異なるような場合です.private のクラス分布がどのようなものになっているかをコンペの意義・目的などからある程度洞察したり,ありえそうなクラス分布の範囲内での QWK の動きをみておくことで,public と private のクラス分布が異なる場合,どれだけの shake がありそうか等の予測をたてておくことはできるかと思います.
この記事が気に入ったらサポートをしてみませんか?
