数学エッセンス　第4回　灘高校数学　令和2年第2問

みなさま、まっちゃんスターです。

今回は、東京大学に続き、灘高校の数学の解説をしたいと思います。

前回に引き続き校門の写真無断転載ではありますが。。。

まあ、あからさまに難易度は高いですが、目安5分といきましょうか。

恒例のごとくまずは問題から。

はい、どうでしょう？

簡単なようにみえてなかなかヘビー級です。

さあ、（１）から参りましょう

（１）PとQについてですが、

Pのｘ　－２ｔ、Pのｙ　４aｔ＾２

QのX＝３ｔ、Qのｙ　９aｔ＾２

これより、

ｘは５ｔ、ｙは５aｔ＾２はなれているとなる。

図ではこうなる。

3の時に、６aｔ＾２なので、

６aｔ＾２＝３より、

aｔ＾２＝1/２

となる。

これで、（１）は終わりました。

さあ、次（２）です。

面積１５ですが、いったんこんなイメージで解けます

図は汚いですが、

左はOの高さ×横なので、

左の面積＋右の面積＝１５

となるので、

２ｔ×３/２＋３ｔ×３/２＝１５

（２＋３）×３ｔ＝15×２＝30

ｔ＝30/１5＝２なので、

ｔ＝２

また、

6aｔ＾２＝３より、

６a×２＾２＝３から

a＝３/２４＝1/８

よって

a＝1/８

これで、（１）と（２）は完成しました。

灘というわりとさくっといったな、おいｗ

さあ、問題の（３）です。

まず、OPRですが、ひとまずイメージ戦略としては

となります。※ペイントなので雑になりましたが、、、

なぜ２と３の数字にしているかというと、問題である２ｔ、３ｔは２と３の倍数に比例するので、まずはベースとなる２と３で考えてます。

面積として考えるのは原点の長さを利用です。

原点は、ｙ＝Rとなる。

これは、ｘ＝２が２、ｘ＝３が４．５より、

ｙ＝ｘ＾２/２のグラフになるので、傾きは１ずつ増えていく（微分は高校の範囲なので、ここでは説明省略）

それにより、２からはRの値が大きくなるごとに３，４，５、と１ずつ増えていく。また、幅は、－２の分の大きさも考慮してOPRは

R（R＋２）・・・OPRの面積※3角形の1/２は省略

で考える

また、台形OQRAは以下のように考えてみる

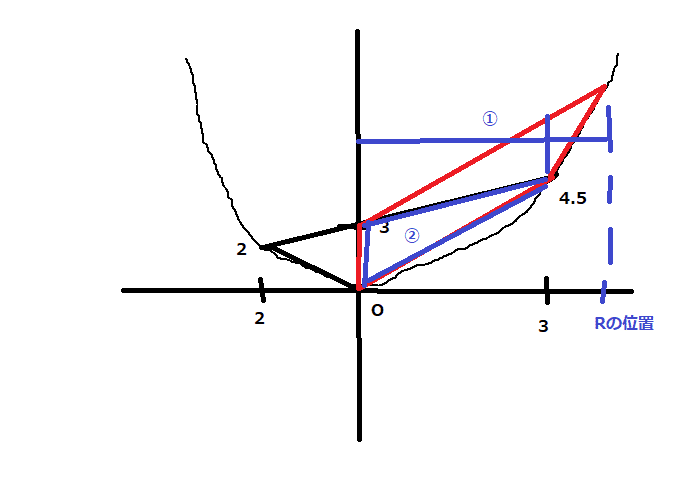
①は、RQA、②はOAQとなる

②については、縦、高さが３なので、

OAQ＝９※1/２約分は省略

Rの傾きは、

（R＾２－６）/２Rと仮定して、

基準３として、３（R＾２－６）/２Rであり、高さ求めるのに補正した３を加えた後、aｘ＾２の３の高さを削除する。

これにより、縦は

（３－４．５）＋３（R＾２－６）/２R＝３（R＾２－R－６）/２R

となる。また、幅R分をかければ①は

３（R＾２－R－６）/２となる

①+②より、

３（R＾２－R－６＋６）/２より

３R（R－１）/２・・・台形OQRA

求めたOPRの面積と台形OQRAより

R（R＋２）＝３R（R－１）/２より、

０＝０．５R＾２－３．５R＝０．５R（R-7)より

R=0,7

ただ、R>3より、R=7

この条件から、問題式のｔに戻すとRの座標は

R＝（７ｔ、４９aｔ＾２）

が答えとなる。

とまあ、灘の問題を開設しました。

うん、このサイトの名称であるエッセンスがいっぱいわかる問題だったかと思います。

感想としては、自分は大学まで出ているので、そこまで難しい感じはしなかったのですが、中学生が特には難しいかという感じですかね。

やはり、普通の中学生ですと、この文章題をどこからさばいていくかがおそらく思いつかない。

というわけで、今回の灘の解説おわり

みなさんもまっちゃんスターに解説してほしい問題あればおしえてください＾＾

ではまだねー😏