
高校数学をプログラミングで解く(数学II編)「1-4 剰余の定理と因数定理」
マガジンリスト > 数学Ⅱ編 1.複素数と方程式 > 1-4 剰余の定理と因数定理
はじめに
今回は、数学IIで学ぶ「剰余の定理と因数定理」について、剰余の定理に関連する問題を解くプログラムや因数定理を応用して因数分解を補助するプログラムを作成します。
剰余の定理と因数定理
まず、剰余の定理と因数定理について解説しておきます。
剰余の定理
① 整式$${P(x)}$$を1次式$${x-k}$$で割ったときの余りは$${P(k)}$$
② 整式$${P(x)}$$を1次式$${ax+b}$$で割ったときの余りは$${P(-b/a)}$$
因数定理
① 1次式$${x-k}$$が整式$${P(x)}$$の因数である$${\Leftrightarrow}$$ $${ P(k)=0}$$
② 1次式$${ax+b}$$が整式$${P(x)}$$の因数である$${\Leftrightarrow}$$ $${ P(-b/a)=0}$$
参考 $${P(x)}$$の最高次の項の係数を$${A}$$、定数項を$${B}$$とすると、$${P(k)=0}$$となる$${k}$$の候補は
$$
\pm \frac{|B|\mathrm{の正の約数}}{|A|\mathrm{の正の約数}}
$$
剰余の定理に関する問題
では剰余の定理に関する下記の問題をプログラミングして解いてみます。
問題1
次の整式を、[ ]内の1次式で割ったときの余りを求めよ。
(1) $${x^2-5x-14}$$ [$${x-2}$$]
(2) $${x^3-x^2-7x-6}$$ [$${x+1}$$]
(3) $${2x^3-x^2-2x+1}$$ [$${2x-1}$$]
(4) $${3x^3-x^2+2}$$ [$${3x+2}$$]
アルゴリズム設計
剰余の定理では、整式$${P(x)}$$に1次式$${x-k}$$や$${ax+b}$$から得られる$${x=k}$$や$${x=-b/a}$$の値を代入して得られた値が剰余になります。つまり、各整式の関数を準備して$${x}$$の値を代入するだけでよいことになります。
プログラム
それでは、問題1を解くプログラムを作成します。各問題の整式を関数として準備し、その関数に値を代入することで計算します。
// 剰余の定理に関する問題
void setup(){
// (1) x^2-5x-14 [x-2]
float x1 = 2.0;
float remainder1 = f1(x1);
println("(1)の剰余:"+ remainder1 );
// (2) x^3-x^2-7x-6 [x+1]
float x2 = -1.0;
float remainder2 = f2(x2);
println("(2)の剰余:"+ remainder2 );
// (3) 2x^3-x^2-2x+1 [2x-1]
float x3 = 1.0/2.0;
float remainder3 = f3(x3);
println("(3)の剰余:"+ remainder3 );
// (4) 3x^3-x^2+2 [3x+2]
float x4 = -2.0/3.0;
float remainder4 = f4(x4);
println("(4)の剰余:"+ remainder4 );
}
// f1(x)=x^2-5x-14
float f1(
float x
){
return x*x-5.0*x-14.0;
}
// f2(x)=x^3-x^2-7x-6
float f2(
float x
){
return x*x*x-x*x-7.0*x-6.0;
}
// f3(x)=2x^3-x^2-2x+1
float f3(
float x
){
return 2.0*x*x*x-x*x-2.0*x+1.0;
}
// f4(x)=3x^3-x^2+2
float f4(
float x
){
return 3.0*x*x*x-x*x+2.0;
}ソースコード1 剰余の定理に関する問題1のプログラム
このソースコード1を、Processingの開発環境ウィンドウを開いて(スケッチ名を「remainder_theorem」としています)、テキストエディタ部分に書いて実行すると、図1のように、
(1)の剰余:-20.0
(2)の剰余:-1.0
(3)の剰余:0.0
(4)の剰余:0.6666665
とコンソールに出力されます。
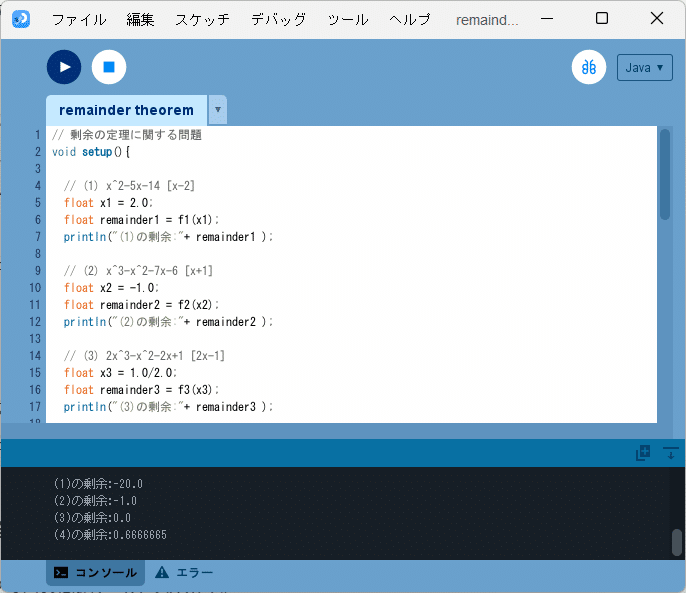
これらの結果が正しいかどうかは手計算で簡単に確認することができるので、やってみてください。
因数分解に関する問題
今度は、因数分解に関する次の問題を考えます。
問題2
次の式を因数分解せよ。
(1) $${x^3-2x^2-x+2}$$
(2) $${x^3-x^2-8x+12}$$
(3) $${2x^3+9x^2+13x+6}$$
(4) $${3x^3-8x^2-15x-4}$$
今回は、これらの整式を直接因数分解するようなプログラムは作成せず、因数分解を補助するプログラムを作成してみます。つまり、上記の「因数分解」の節に「参考」として記載した『$${P(k)=0}$$となる$${k}$$の候補』を探すプログラムを作成します。
アルゴリズム設計
『$${P(k)=0}$$となる$${k}$$の候補』を探すためには、因数分解したい整式$${P(x)}$$の最高次の項の係数$${A}$$の絶対値の約数と定数項$${B}$$の絶対値の約数のすべての組合せに対して
$$
k=\pm \frac{|B|\mathrm{の正の約数}}{|A|\mathrm{の正の約数}}
$$
を計算し、$${P(k)=0}$$が成り立つかどうかを判定します。$${P(k)=0}$$が成り立っていれば、そのときの$${k}$$が『$${P(k)=0}$$となる$${k}$$の候補』となります。
プログラム
それでは、問題2(1)を例にして、『$${P(k)=0}$$となる$${k}$$の候補』を探すプログラムを作成していきます。
// 因数定理に関する問題
void setup(){
// 整式の最高次の項の係数の絶対値
int A = 1;
// 整式の定数項の絶対値
int B = 2;
// Aの約数
ArrayList<Integer> divisor_A = new ArrayList<Integer>();
for(int i=1; i<=A; i++){
if( A%i == 0 ){
divisor_A.add(i);
}
}
// Bの約数
ArrayList<Integer> divisor_B = new ArrayList<Integer>();
for(int i=1; i<=B; i++){
if( B%i == 0 ){
divisor_B.add(i);
}
}
// P(k)=0となるkの候補
float candidate_k;
for(int i=0; i<divisor_A.size(); i++){
for(int j=0; j<divisor_B.size(); j++){
for(int k=0; k<=1; k++){
candidate_k =pow(-1.0, k)*(float)divisor_B.get(j)/divisor_A.get(i);
if( P(candidate_k) == 0.0 ){
println(candidate_k);
}
}
}
}
}
// P(x)=x^3-2x^2-x+2
float P(
float x
){
return x*x*x-2.0*x*x-x+2.0;
}ソースコード2 『$${P(k)=0}$$となる$${k}$$の候補』を探すプログラム
このソースコード2を、Processingの開発環境ウィンドウを開いて(スケッチ名を「factor_theorem」としています)、テキストエディタ部分に書いて実行すると、図2のように、
1.0
-1.0
2.0
とコンソールに出力されます。
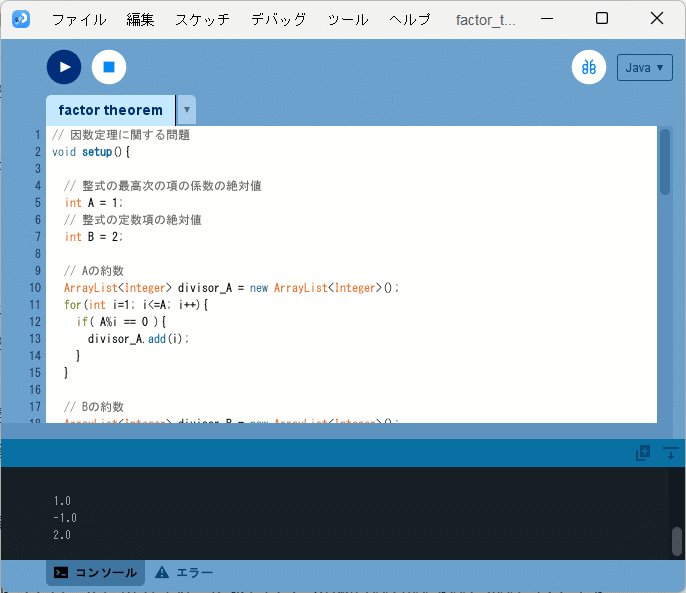
これらの$${k}$$の候補に関する結果を用いると、問題2(1)の整式は、
$$
x^3-2x^2-x+2 = (x+1)(x-1)(x-2)
$$
と因数分解できることがわかります。
問題2(2)の因数分解
では、次に『$${P(k)=0}$$となる$${k}$$の候補』を探すプログラム(ソースコード2)を利用して、問題2(2)の因数分解を考えます。
そのために、ソースコード2の変数A, Bと関数$${P(x)}$$の部分を書き換えて、問題2(2)に合わせます。
// 因数定理に関する問題
void setup(){
// 整式の最高次の項の係数の絶対値
int A = 1;
// 整式の定数項の絶対値
int B = 12;
// Aの約数
ArrayList<Integer> divisor_A = new ArrayList<Integer>();
for(int i=1; i<=A; i++){
if( A%i == 0 ){
divisor_A.add(i);
}
}
// Bの約数
ArrayList<Integer> divisor_B = new ArrayList<Integer>();
for(int i=1; i<=B; i++){
if( B%i == 0 ){
divisor_B.add(i);
}
}
// P(k)=0となるkの候補
float candidate_k;
for(int i=0; i<divisor_A.size(); i++){
for(int j=0; j<divisor_B.size(); j++){
for(int k=0; k<=1; k++){
candidate_k =pow(-1.0, k)*(float)divisor_B.get(j)/divisor_A.get(i);
if( P(candidate_k) == 0.0 ){
println(candidate_k);
}
}
}
}
}
// P(x)=x^3-x^2-8x+12
float P(
float x
){
return x*x*x-x*x-8.0*x+12.0;
}ソースコード3 ソースコード2を問題2(2)に合わせて調整
スケッチ「factor_theorem」をソースコード3に書き換えて実行すると、図3のように、
2.0
-3.0
とコンソールに出力されます。
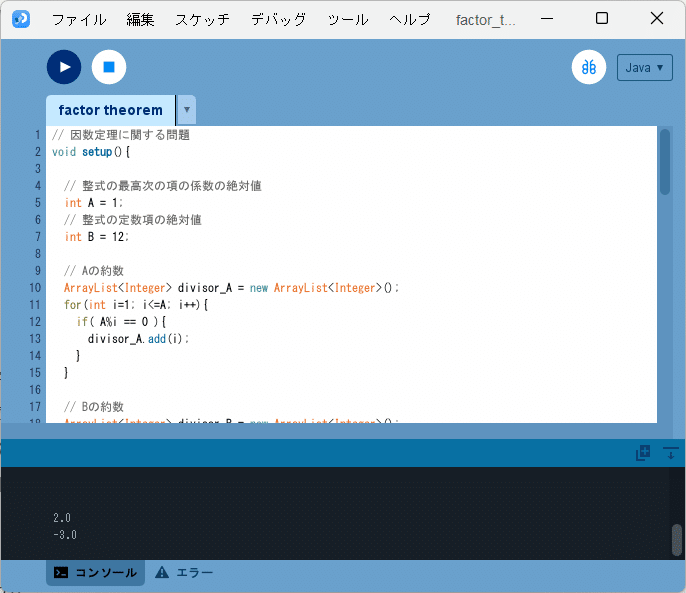
これらの$${k}$$の候補に関する結果を用いると、問題2(2)の整式は、
$$
x^3-x^2-8x+12 = (x-2)(x+3)(x-k)
$$
の形に因数分解できることがわかります。残りの$${k}$$は、
$$
(-2)\cdot 3 \cdot (-k) = 12
$$
となることを考慮すると$${k=2}$$となり、問題2(2)の因数分解は、
$$
x^3-x^2-8x+12 = (x-2)^2(x+3)
$$
となることがわかります。
問題2(3)の因数分解
今度は、問題2(3)を考えてみます。ソースコード2の変数A, Bと関数$${P(x)}$$の部分を書き換えて、問題2(3)に合わせます。
// 因数定理に関する問題
void setup(){
// 整式の最高次の項の係数の絶対値
int A = 2;
// 整式の定数項の絶対値
int B = 6;
// Aの約数
ArrayList<Integer> divisor_A = new ArrayList<Integer>();
for(int i=1; i<=A; i++){
if( A%i == 0 ){
divisor_A.add(i);
}
}
// Bの約数
ArrayList<Integer> divisor_B = new ArrayList<Integer>();
for(int i=1; i<=B; i++){
if( B%i == 0 ){
divisor_B.add(i);
}
}
// P(k)=0となるkの候補
float candidate_k;
for(int i=0; i<divisor_A.size(); i++){
for(int j=0; j<divisor_B.size(); j++){
for(int k=0; k<=1; k++){
candidate_k =pow(-1.0, k)*(float)divisor_B.get(j)/divisor_A.get(i);
if( P(candidate_k) == 0.0 ){
println(candidate_k);
}
}
}
}
}
// P(x)=2x^3+9x^2+13x+6
float P(
float x
){
return 2.0*x*x*x+9.0*x*x+13.0*x+6.0;
}ソースコード4 ソースコード2を問題2(3)に合わせて調整
スケッチ「factor_theorem」をソースコード4に書き換えて実行すると、図4のように、
-1.0
-2.0
-1.0
-1.5
とコンソールに出力されます。
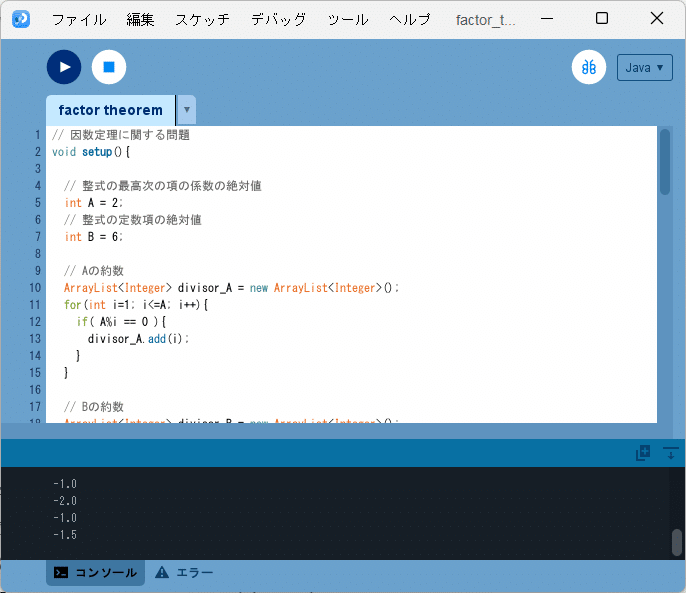
$${k}$$の候補として、$${-1}$$が2回出てきています。これは$${|A|}$$の約数が$${1,2}$$、$${|B|}$$の約数が$${1,2,3,6}$$ですので、最初の$${-1}$$は$${k=-1/1}$$から求められたもので、2つ目の$${-1}$$は$${k=-2/2}$$から求められたもので、2つとも同じものになります。
これらの$${k}$$の候補に関する結果を用いると、問題2(3)の整式は、
$$
\begin{array}{ll}
2x^3+9x^2+13x+6 &=2(x+1)(x+2)(x+1.5) \\
&=(x+1)(x+2)(2x+3)
\end{array}
$$
と因数分解できることがわかります。
問題2(4)の因数分解
最後に、問題2(4)を考えてみます。ソースコード2の変数A, Bと関数$${P(x)}$$の部分を書き換えて、問題2(4)に合わせます。
// 因数定理に関する問題
void setup(){
// 整式の最高次の項の係数の絶対値
int A = 3;
// 整式の定数項の絶対値
int B = 4;
// Aの約数
ArrayList<Integer> divisor_A = new ArrayList<Integer>();
for(int i=1; i<=A; i++){
if( A%i == 0 ){
divisor_A.add(i);
}
}
// Bの約数
ArrayList<Integer> divisor_B = new ArrayList<Integer>();
for(int i=1; i<=B; i++){
if( B%i == 0 ){
divisor_B.add(i);
}
}
// P(k)=0となるkの候補
float candidate_k;
for(int i=0; i<divisor_A.size(); i++){
for(int j=0; j<divisor_B.size(); j++){
for(int k=0; k<=1; k++){
candidate_k =pow(-1.0, k)*(float)divisor_B.get(j)/divisor_A.get(i);
if( P(candidate_k) == 0.0 ){
println(candidate_k);
}
}
}
}
}
// P(x)=3x^3-8x^2-15x-4
float P(
float x
){
return 3.0*x*x*x-8.0*x*x-15.0*x-4.0;
}
ソースコード5 ソースコード2を問題2(4)に合わせて調整
スケッチ「factor_theorem」をソースコード5に書き換えて実行すると、図5のように、
-1.0
4.0
-0.33333334
とコンソールに出力されます。
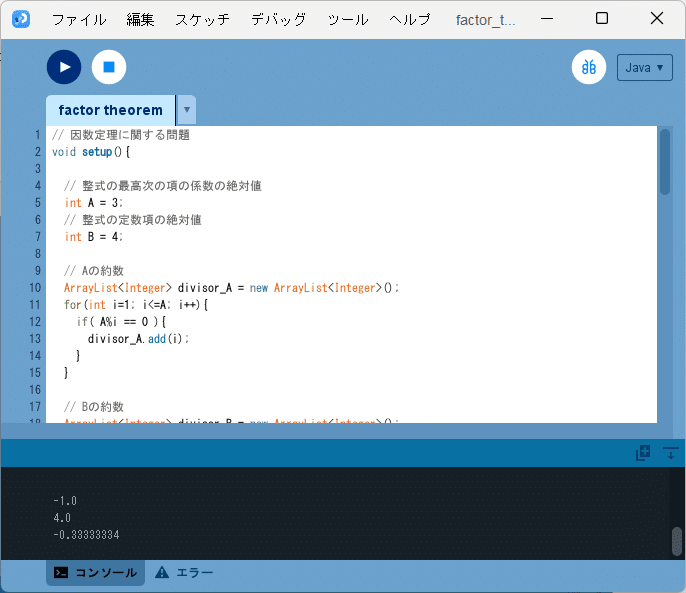
これらの$${k}$$の候補に関する結果を用いると、問題2(4)の整式は、
$$
\begin{array}{ll}
3x^3-8x^2-15x-4 &=3(x+1)(x-4)(x+1/3) \\
&=(x+1)(x-4)(3x+1)
\end{array}
$$
と因数分解できることがわかります。
まとめ
今回は、数学IIで学ぶ「剰余の定理と因数定理」について、剰余の定理に関連する問題を解くプログラムや因数定理を応用して因数分解を補助するプログラムを作成しました。
問題1は、整式$${P(x)}$$を関数として準備し、1次式$${x-k}$$の$${k}$$の値を$${P(x)}$$に代入するだけですので、簡単に解くことができました。
問題2は、因数定理を応用して因数分解を補助するプログラム、つまり整式$${P(x)}$$に対して『$${P(k)=0}$$となる$${k}$$の候補』を探すプログラムを作成し、その結果を用いて$${P(x)}$$を因数分解するということを行いました。
因数分解は数学Iで出てきますが、これまで扱ってきませんでした。それは、『整式を因数分解させるプログラム』を作成することは結構難しいと考えているからです。でも、今回のように因数分解を補助するようなプログラムは考えることができます。プログラムはこのような使い方もできますので、様々な場面でプログラムの応用を考えてみてください。
参考文献
改訂版 教科書傍用 スタンダード 数学II(数研出版、ISBN9784410209369)
