高校数学をプログラミングで解く(数学II編)「2-5 軌跡と方程式」
はじめに
今回は、数学IIで学ぶ「軌跡と方程式」について、ある条件を満たす点をプロットすることで軌跡を描いていくプログラムを作成します。
軌跡と方程式
まず、軌跡と方程式について解説しておきます。
軌跡の証明法
与えられた条件を満たす点$${\mathrm{P}}$$の軌跡が図形$${F}$$であることの証明。
[1] その条件を満たす任意の点$${\mathrm{P}}$$が、図形$${F}$$上にあること
[2] 図形$${F}$$上の任意の点$${\mathrm{P}}$$が、その条件を満たすこと
平面上の軌跡の求め方
[1] 座標軸を計算がしやすいように定める。
[2] 求める軌跡上の任意の点の座標を$${(x,y)}$$などで表し、与えられた条件を座標間の関係式(方程式)で表す。
[3] 軌跡の方程式を導き、その方程式の表す図形を求める。
[4] その図形上の点が条件を満たしているかどうかを確かめる。
※注意 [4]が明らかな場合は、これを省略することがある。
軌跡を描く
今回は、ある条件を満たす任意の点の軌跡を描くプログラムを作成していきます。
問題
次の条件を満たす点$${\mathrm{P}}$$の軌跡をキャンバス上に描け。
(1) 点$${(1,2)}$$からの距離が$${3}$$である点$${\mathrm{P}}$$
(2) $${x}$$軸との距離$${3}$$である点$${\mathrm{P}}$$
(3) $${\mathrm{O}}$$を原点とするとき、直線$${\mathrm{OP}}$$の傾きが$${2}$$である点$${\mathrm{P}}$$
(4) 2定点$${ \mathrm{A}(-1,0), \ \mathrm{B}(1,0) }$$に対して、$${\angle \mathrm{APB}=90^{\circ} }$$となる点$${\mathrm{P}}$$
なお、この問題を解くにあたって「軌跡の方程式を導いてその方程式の表す図形を描く」という手順は取らないことにします。今回はキャンバスの描画範囲内の任意の点$${(x,y)}$$を取ってきて、その点が与えられた条件を満たすかどうかを確かめ、条件を満たしていればその点をキャンバス上にプロットし、条件を満たしていなければプロットしないというルールで行います。そして、プロットされた点が描く軌跡がどのような図形(方程式)になっているかを見てみます。
問題(1)のアルゴリズム設計
問題(1)を少し一般化して定式化してみます。
点$${(x_1, y_1)}$$からの距離を$${d}$$とします。また、任意の点$${(x,y)}$$と点$${(x_1, y_1)}$$とを結んだ線分の長さ$${l}$$とすると、
$$
l = \sqrt{(x-x_1)^2+(y-y_1)^2}
$$
で計算することができます。したがって、問題(1)の条件は「$${l}$$と$${d}$$とが等しい」ということができます。
ただ、この条件をプログラミングする際には、もう少し工夫が必要になります。実際のプログラムでは、任意の点$${(x,y)}$$は random 関数を利用して取得します。このように取得した点から$${l}$$を計算して$${d}$$と比較した場合、厳密に$${l}$$と$${d}$$とが等しくなるようなことはほとんど起こらないでしょう。つまり、プログラム内において
l == dという条件を満たす点は現れないでしょう。
そこで、条件を少し緩めることにします。つまり、ある程度小さな値をもつマージン$${e}$$を用意して「$${l}$$と$${d}$$とが等しい」という条件を「$${l}$$が$${d-e}$$と$${d+e}$$との間に入っている」という条件に緩めることにします。この条件を式で表すと、
abs(l-d) < eと書くことができます。
問題(1)のプログラム
それでは、問題(1)の条件を満たす軌跡を描くプログラムを作成します。今回は、setAxes.pdeファイルと座標$${(x,y)}$$に点をプロットする関数 plot_point を再利用したいので、記事『高校数学をプログラミングで解く(数学II編)「2-3 円の方程式」』で作成したスケッチ「drawCircles」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawTrajectory1」と変更し、またスケッチ「drawTrajectory1」内の「drawCircles.pde」ファイルの名前を「drawTrajectory1.pde」に変更します。そして、pdeファイル「drawTrajectory1.pde」をダブルクリックしてスケッチ「drawTrajectory1」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawTrajectory1」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// 点(1,2)
float x1 = 1.0;
float y1 = 2.0;
// 距離 3
float d = 3.0;
// 点の生成回数
int n = 1000000;
// マージン
float e = 0.001;
float x, y; // 任意の点の座標
float l; // 点(x1, y1)からの距離
for(int i=0; i<n; i++){
x = random(-x_range, x_range);
y = random(-y_range, y_range);
l = sqrt((x-x1)*(x-x1)+(y-y1)*(y-y1));
if( abs(l-d) < e ){
plot_point(x,y);
}
}
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード1 問題(1)の条件を満たす軌跡を描くプログラム
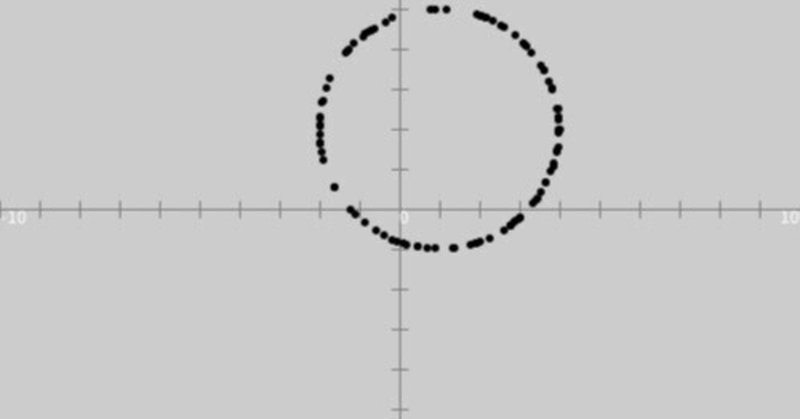
ソースコード1を、スケッチ「drawTrajectory1」の「drawTrajectory1」タブのテキストエディタ部分に書いて実行すると、図1のように、実行ウィンドウのキャンバス上に問題(1)の条件を満たす点が描かれます。

図1を見ると、問題(1)の条件を満たす点の軌跡は円を描くことがわかります。また、軌跡の方程式は円の方程式$${(x-1)^2+(y-2)^2=3^2}$$になっていることも図形から推察できます。
問題(2)のアルゴリズム設計
次に、問題(2)を考えます。こちらも少し一般化して定式化してみます。
$${x}$$軸からの距離を$${d}$$とします。また、任意の点$${(x,y)}$$と$${x}$$軸との距離を$${l}$$とすると、
$$
l = |y|
$$
で計算することができます。したがって、問題(2)の条件は「$${l}$$と$${d}$$とが等しい」ということができますが、今回も条件を少し緩めて、「$${l}$$が$${d-e}$$と$${d+e}$$との間に入っている」という条件にします。式で表すと、
abs(l-d) < eとなります。
問題(2)のプログラム
では、問題(2)の条件を満たす点の軌跡を描くプログラムを作成します。先ほど作成したスケッチ「drawTrajectory1」を再利用します。
スケッチ「drawTrajectory1」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawTrajectory2」と変更し、またスケッチ「drawTrajectory2」内の「drawTrajectory1.pde」ファイルの名前を「drawTrajectory2.pde」に変更します。そして、pdeファイル「drawTrajectory2.pde」をダブルクリックしてスケッチ「drawTrajectory2」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawTrajectory2」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// 距離 3
float d = 3.0;
// 点の生成回数
int n = 1000000;
// マージン
float e = 0.001;
float x, y; // 任意の点の座標
float l; // x軸からの距離
for(int i=0; i<n; i++){
x = random(-x_range, x_range);
y = random(-y_range, y_range);
l = abs(y);
if( abs(l-d) < e ){
plot_point(x,y);
}
}
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード2 問題(2)の条件を満たす軌跡を描くプログラム
ソースコード2を、スケッチ「drawTrajectory2」の「drawTrajectory2」タブのテキストエディタ部分に書いて実行すると、図2のように、実行ウィンドウのキャンバス上に問題(2)の条件を満たす点が描かれます。

図2を見ると、問題(2)の条件を満たす点の軌跡は2つの直線を描くことがわかります。また、軌跡の方程式は直線の方程式$${y=3}$$と$${y=-3}$$になっていることも図形から推察できます。
問題(3)のアルゴリズム設計
次に、問題(3)を考えます。こちらも少し一般化して定式化してみます。
直線の傾きを$${m}$$とします。また、任意の点$${(x,y)}$$と原点と通る直線の傾きを$${a}$$とすると、
$$
a = \frac{y}{x}
$$
で計算することができます。したがって、問題(3)の条件は「$${a}$$と$${m}$$とが等しい」ということができますが、この条件を少し緩めて、「$${a}$$が$${m-e}$$と$${m+e}$$との間に入っている」という条件にします。式で表すと、
abs(a-m) < eとなります。
問題(3)のプログラム
では、問題(3)の条件を満たす点の軌跡を描くプログラムを作成します。こちらもスケッチ「drawTrajectory1」を再利用します。
スケッチ「drawTrajectory1」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawTrajectory3」と変更し、またスケッチ「drawTrajectory3」内の「drawTrajectory1.pde」ファイルの名前を「drawTrajectory3.pde」に変更します。そして、pdeファイル「drawTrajectory3.pde」をダブルクリックしてスケッチ「drawTrajectory3」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawTrajectory3」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// 直線の傾き 2
float m = 2.0;
// 点の生成回数
int n = 1000000;
// マージン
float e = 0.001;
float x, y; // 任意の点の座標
float a; // OPの傾き
for(int i=0; i<n; i++){
x = random(-x_range, x_range);
y = random(-y_range, y_range);
a = y/x;
if( abs(a-m) < e ){
plot_point(x,y);
}
}
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード3 問題(3)の条件を満たす軌跡を描くプログラム
ソースコード3を、スケッチ「drawTrajectory3」の「drawTrajectory3」タブのテキストエディタ部分に書いて実行すると、図3のように、実行ウィンドウのキャンバス上に問題(3)の条件を満たす点が描かれます。

図3を見ると、問題(3)の条件を満たす点の軌跡は直線を描くことがわかります。また、軌跡の方程式は直線の方程式$${y=2x}$$になっていることも図形から推察できます。
問題(4)のアルゴリズム設計
最後に、問題(4)を考えます。
まず、条件式$${\angle \mathrm{APB}=90^{\circ} }$$を書き換えると、
$$
\cos ( \angle \mathrm{APB} ) = \cos 90^{\circ} = 0
$$
となります。一方、2定点を$${ \mathrm{A}(x_1,y_1), \ \mathrm{B}(x_2,y_2) }$$とし、任意の点$${\mathrm{P}(x,y)}$$とすると、
$$
\begin{array}{ll}
\cos ( \angle \mathrm{APB} ) &= \frac{\overrightarrow{\mathrm{AP}} \cdot \overrightarrow{\mathrm{BP}}}{|\overrightarrow{\mathrm{AP}}| \cdot |\overrightarrow{\mathrm{BP}}|} \\ &=\frac{(x-x_1)(x-x_2)+(y-y_1)(y-y_2)}{\sqrt{(x-x_1)^2+(y-y_1)^2} \sqrt{(x-x_2)^2+(y-y_2)^2}}
\end{array}
$$
で計算することができます。したがって、問題(4)の条件は「$${\cos ( \angle \mathrm{APB} )}$$が$${0}$$に等しい」ということができますが、この条件を少し緩めて、「$${\cos ( \angle \mathrm{APB} )}$$が$${-e}$$と$${e}$$との間に入っている」という条件にします。
問題(4)のプログラム
では、問題(4)の条件を満たす点の軌跡を描くプログラムを作成します。こちらもスケッチ「drawTrajectory1」を再利用します。
スケッチ「drawTrajectory1」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawTrajectory4」と変更し、またスケッチ「drawTrajectory4」内の「drawTrajectory1.pde」ファイルの名前を「drawTrajectory4.pde」に変更します。そして、pdeファイル「drawTrajectory4.pde」をダブルクリックしてスケッチ「drawTrajectory4」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawTrajectory4」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// 点A(x1,y1)
float x1 = -1.0;
float y1 = 0.0;
// 点B(x2,y2)
float x2 = 1.0;
float y2 = 0.0;
// 角度 90°
float angle = 90.0;
// cos(90°)
float cos90 = cos(radians(angle));
// 点の生成回数
int n = 10000000;
// マージン
float e = 0.001;
float x, y; // 任意の点の座標
float innerproduct; // ベクトルPAとPBの内積
float absPA, absPB; // ベクトルPAとPBの大きさ
float cosAPB; // cos(∠APB)
for(int i=0; i<n; i++){
x = random(-x_range, x_range);
y = random(-y_range, y_range);
innerproduct = (x1-x)*(x2-x)+(y1-y)*(y2-y);
absPA = sqrt((x1-x)*(x1-x)+(y1-y)*(y1-y));
absPB = sqrt((x2-x)*(x2-x)+(y2-y)*(y2-y));
cosAPB = innerproduct / absPA / absPB;
if( abs(cosAPB-cos90) < e ){
plot_point(x,y);
}
}
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード4 問題(4)の条件を満たす軌跡を描くプログラム
ソースコード3を、スケッチ「drawTrajectory4」の「drawTrajectory4」タブのテキストエディタ部分に書いて実行すると、図4のように、実行ウィンドウのキャンバス上に問題(4)の条件を満たす点が描かれます。

図4を見ると、問題(4)の条件を満たす点の軌跡は円を描くことがわかります。また、軌跡の方程式は円の方程式$${x^2+y^2=1}$$になっていることも図形から推察できます。
まとめ
今回は、数学IIで学ぶ「軌跡と方程式」について、ある条件を満たす点をプロットすることで軌跡を描いていくプログラムを作成しました。
最初の方で、与えられた条件を満たす点についてその軌跡の方程式を導く方法を解説しましたが、今回作成したプログラムでは、方程式を導くことをせず、任意の点をランダムに取ってきて、その点が条件を満たせばプロットしていくことを繰り返すことで、所望の軌跡を描いていきました。
今回扱った問題は、本来方程式を導いてそれを描く方が簡単かもしれませんが、条件が複雑になった場合などは方程式が簡単に見つからないこともあり、今回行った方法も有効になるでしょう。そのため、両方で考えることができるようにしておいてください。
参考文献
改訂版 教科書傍用 スタンダード 数学II(数研出版、ISBN9784410209369)
この記事が気に入ったらサポートをしてみませんか?
