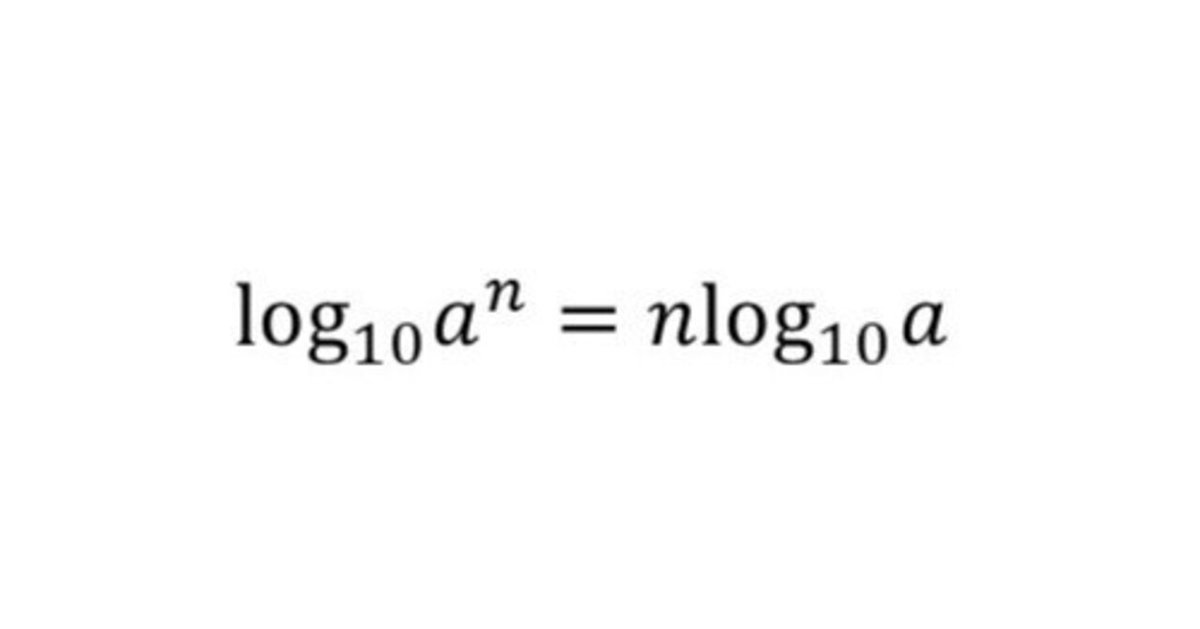
高校数学をプログラミングで解く（数学II編）「4-5 常用対数」

マガジンリスト　＞　数学Ⅱ編 4.指数関数と対数関数　＞　4-5 常用対数

はじめに

今回は、数学IIで学ぶ「常用対数」について、与えられた数の常用対数を計算してその数の桁数を求めるプログラムを作成します。

常用対数

まず、常用対数について解説しておきます。

常用対数

$${10}$$を底とする対数を常用対数という。

$${x = a \times 10^n}$$（$${n}$$は整数、$${1 \leq a <10}$$）とすると、$${ \log_{10} x = n + \log_{10} a }$$

桁数と対数

① $${N \geq 1}$$

$${N}$$の整数部分が$${n}$$桁
$${ \Leftrightarrow }$$  $${10^{n-1} \leq N < 10^n}$$
$${ \Leftrightarrow }$$  $${\log_{10} N}$$の整数部分が$${n-1}$$

② $${0 < N <1}$$

$${N}$$は小数第$${n}$$位に初めて$${0}$$でない数字が現れる
$${ \Leftrightarrow }$$  $${ 10^{-n} \leq N < 10^{-n+1} }$$
$${ \Leftrightarrow }$$  $${\log_{10} N}$$の整数部分が$${-n}$$

桁数を計算する

今回は、次の数の桁数を計算するプログラムを作成します。

問題
次の(1)～(3)の値は何桁の数か。また、(4),(5)の値は小数第何位に初めて$${0}$$でない数字が現れるか。
(1) $${ 2^{50} }$$
(2) $${ 6^{40} }$$
(3) $${ \sqrt[3]{ 12^{100} } }$$
(4) $${ \left( \frac{1}{2} \right)^{100} }$$
(5) $${ \sqrt[3]{ (0.06)^{10} } }$$

アルゴリズム設計

記事『高校数学をプログラミングで解く（数学II編）「4-3 対数とその性質」』で解説したように、Processingでは、任意の底を持つような対数を計算する関数や常用対数を計算する関数は用意されておらず、自然対数と呼ばれる底$${e = 2.718 \cdots }$$の対数を計算する関数 log のみ用意されています。

log(x);

x：真数　float型
返り値：xの自然対数の値　float型

つまり、この関数 log は、$${ \log_e x}$$の値を返します。
そこで、記事『高校数学をプログラミングで解く（数学II編）「4-3 対数とその性質」』のスケッチ「calc_logarithms」の中で作成した logarithm 関数を再利用します。この logarithm 関数は対数の性質③底の変換公式を利用すると、

$$
\log_a x = \frac{ \log_e x}{ \log_e a}
$$

と変換することができるので、底$${a}$$を持つ対数を計算する関数 logarithm は、

// 底aを持つ対数を計算する関数
float logarithm(
  float a, // 底
  float x  // 真数
){
  return log(x)/log(a);
}

と書くことができました。この logarithm 関数の底$${a}$$に$${10}$$を代入することで常用対数を計算することができます。

この logarithm 関数を用いて、問題の値の常用対数を計算し、桁数等を求めていきます。ただ、今回扱っている問題の値は結構大きな数（int型で扱える整数の値を超える）となるため、それらの値の常用対数を直接求めないようにしました。つまり、数$${a^n}$$に対して、常用対数は

$$
\log_{10} a^n = n \times \log_{10} a
$$

となるので、この式の左辺の値を計算するのではなく、右辺の値を計算することにします。この常用対数を計算すると、上記で解説した桁数と対数の性質を利用して、問題の桁数を計算することができます。
なお、問題(3)と(5)については、

(3) $${ \sqrt[3]{ 12^{100} }= (12)^{\frac{100}{3}} }$$
(5) $${ \sqrt[3]{ (0.06)^{10} } = (0.06)^{\frac{10}{3}} }$$

と変形できることを利用して桁数の計算を行います。

プログラム

それでは、数の桁数を計算するプログラムを作成します。

// 常用対数を計算して桁数を求める
void setup(){

  // (1) 
  int a01 = calc_digits(2.0, 50.0);
  println("(1):", a01,"桁");
  
  // (2)
  int a02 = calc_digits(6.0, 40.0);
  println("(2):", a02,"桁");

  // (3)
  int a03 = calc_digits(12.0, 100.0/3.0);
  println("(3):", a03,"桁");
  
  // (4)
  int a04 = calc_digits(0.5, 100.0);
  println("(4):", "小数第",a04,"位");

  // (5)
  int a05 = calc_digits(0.06, 10.0/3.0);
  println("(5):","小数第",a05,"位");

}

// 底aを持つ対数を計算する関数
float logarithm(
  float a, // 底
  float x  // 真数
){
  return log(x)/log(a);
}

// a^nの桁数を求める関数
int calc_digits(
  float a, // 底
  float n  // 冪指数
){
  // 常用対数を計算する
  float cl = n * logarithm(10.0, a);
  // 常用対数の整数部分
  int int_part = floor(cl);
  int digits;
  if( cl > 0.0 ){
    // a^n はint_part+1 桁の整数
    digits = int_part + 1;
  } else {
    // a^n は小数第 -int_part 位に初めて0が出てくる小数
    digits = -int_part;
  }
  return digits;
}

ソースコード1　数の桁数を計算するプログラム

ソースコード1を、Processingの開発環境ウィンドウを開いて（スケッチ名を「calc_common_logarithms」としています）、テキストエディタ部分に書いて実行します。

図1　スケッチ「calc_common_logarithms」の実行結果

図1のように、コンソールに各問題の値の桁数が出力されます。

(1): 16 桁
(2): 32 桁
(3): 36 桁
(4): 小数第 31 位
(5): 小数第 5 位

これらの結果は正しく得られていますが、念のため、ご自身で解析的に計算した結果と比較しておいてください。

まとめ

今回は、数学IIで学ぶ「常用対数」について、与えられた数の常用対数を計算してその数の桁数を求めるプログラムを作成しました。
今回の計算では、桁数を求めたい値$${a^n}$$が比較的大きいもの（int型で扱える整数の値を超える）であることを考慮して、その常用対数

$$
\log_{10} a^n = n \times \log_{10} a
$$

の左辺ではなく、右辺の値を計算して桁数を求めるようにしました。ただ、今回の問題の場合、桁数を知りたいだけなので、$${a^n}$$を正確に整数として計算する必要はなく、浮動小数点数（小数）で桁数を求めるために必要な計算をするだけでもよいと思います。つまり、問題の値を pow 関数を用いて浮動小数点数として計算してから上記式の左辺を直接計算することで桁数を計算することができます。こちらの方法でも是非計算してみてください。

参考文献

改訂版 教科書傍用 スタンダード 数学II（数研出版、ISBN9784410209369）