
高校数学をプログラミングで解く(数学II編)「1-3 解と係数の関係」
マガジンリスト > 数学Ⅱ編 1.複素数と方程式 > 1-3 解と係数の関係
はじめに
今回は、数学IIで学ぶ「解と係数の関係」について、2次方程式の解と係数の関係に関連するいくつかの問題をプログラミングして解いてみます。
解と係数の関係
まず、解と係数の関係について解説しておきます。
2次方程式の解と係数の関係
$${a,b,c}$$は定数、$${a \neq 0}$$とします。
$$
a x^2+bx+c=0 \mathrm{の2つの解が} \alpha, \beta
$$
$$
\Leftrightarrow \alpha + \beta = -\frac{b}{a}, \ \alpha \beta = \frac{c}{a}
$$
$$
\Leftrightarrow ax^2+bx+c = a(x-\alpha)(x-\beta)
$$
2次方程式の作成
① 2つの数$${\alpha, \beta}$$を解とする2次方程式の1つは$${(x-\alpha)(x-\beta)=0}$$
② 和が$${p}$$、積が$${q}$$の2つの数は、2次方程式$${x^2-px+q=0}$$の2つの解。
以下で、2次方程式の解と係数の関係に関する問題をプログラミングして解いていきます。
解と係数の関係の問題1
では、1つ目の問題を考えてみます。
問題1
方程式$${2x^2-2x+1=0}$$の2つの解が$${\alpha, \beta}$$のとき、次の式の値を求めよ。
(1) $${\alpha^2 \beta + \alpha \beta^2}$$
(2) $${\alpha^2+\beta^2}$$
(3) $${(\alpha - \beta)^2}$$
(4) $${(1+\alpha)(1+\beta)}$$
(5) $${\alpha^3+\beta^3}$$
(6) $${\frac{\beta^2}{\alpha}+\frac{\alpha^2}{\beta}}$$
解析的な解法
この問題1は、解と係数の関係から$${\alpha + \beta = -(-2)/2=1, \alpha \beta = 1/2}$$が得られるので、
(1) $${\alpha^2 \beta + \alpha \beta^2 = \alpha \beta(\alpha + \beta) = 1/2 \cdot 1 = 1/2}$$
(2) $${\alpha^2+\beta^2 = (\alpha + \beta)^2 - 2 \alpha \beta = 1^2-2\cdot(1/2) = 0 }$$
(3) $${(\alpha - \beta)^2 = (\alpha + \beta)^2 - 4 \alpha \beta = 1^2 - 4 \cdot (1/2) = -1}$$
(4) $${(1+\alpha)(1+\beta) = 1 + (\alpha+\beta) + \alpha \beta = 1+1+1/2= 5/2}$$
(5) $${\alpha^3+\beta^3 = (\alpha + \beta)^3-3\alpha \beta (\alpha+\beta) = 1^3 -3 \cdot (1/2) \cdot 1 = -1/2}$$
(6) $${\frac{\beta^2}{\alpha}+\frac{\alpha^2}{\beta} = \frac{ \alpha^3+\beta^3}{\alpha \beta} = (-1/2)/(1/2) = -1}$$
と、解析的に計算することができます。ただ、今回作成するプログラムでは、解と係数の関係は利用せずに2次方程式の解である$${\alpha, \beta}$$を実際に算出して各式に代入する方法で計算してみます。これにより、解と係数の関係が成り立っていることが確認できます。
アルゴリズム設計
まず、2次方程式の解である$${\alpha}$$と$${\beta}$$を求めます。それには記事『高校数学をプログラミングで解く(数学II編)「1-2 2次方程式の解と判別式」』で説明した、2次方程式の解の公式を用いて算出します。この問題の2次方程式の判別式は$${-4}$$となり負の値を持つので、$${\alpha,\beta}$$は虚数解、つまり複素数になることがわかります。そのため、この問題の各式の値は、記事『高校数学をプログラミングで解く(数学II編)「1-1 複素数」』で解説したものと同じように、複素数である$${\alpha,\beta}$$をPVectorクラスで表し、複素数の四則演算を行うための関数を再利用して計算することにします。
プログラム
それでは、問題1を解くプログラムを作成します。
// 解と係数の関係1
void setup(){
// 2次方程式の係数
float a = 2.0;
float b = -2.0;
float c = 1.0;
// 2次方程式 2x^2-2x+1=0の解
float x_r = -b/2.0/a;
float x_i = abs(sqrt(abs(b*b-4.0*a*c))/2.0/a);
PVector alpha = new PVector(x_r, x_i);
PVector beta = new PVector(x_r, -x_i);
// (1) a1 = alpha^2 beta + alpha beta^2
PVector a1 = c_sum(c_prod(c_prod(alpha,alpha),beta),c_prod(alpha,c_prod(beta,beta)));
println("(1)"+ a1.x + "+" + a1.y + "i" );
// (2) a2 = alpha^2 + beta^2
PVector a2 = c_sum(c_prod(alpha,alpha),c_prod(beta,beta));
println("(2)"+ a2.x + "+" + a2.y + "i" );
// (3) a3 = (alpha - beta)^2
PVector a3 = c_prod(c_sub(alpha,beta),c_sub(alpha,beta));
println("(3)"+ a3.x + "+" + a3.y + "i" );
// (4) a4 = (1 + alpha)(1 + beta)
PVector unit = new PVector(1.0,0.0);
PVector a4 = c_prod(c_sum(unit,alpha),c_sum(unit,beta));
println("(4)"+ a4.x + "+" + a4.y + "i" );
// (5) a5 = alpha^3 + beta^3
PVector a5 = c_sum(c_prod(c_prod(alpha,alpha),alpha),c_prod(beta,c_prod(beta,beta)));
println("(5)"+ a5.x + "+" + a5.y + "i" );
// (6) a6 = beta^2/alpha + alpha^2/beta
PVector a6 = c_sum(c_div(c_prod(beta,beta),alpha), c_div(c_prod(alpha,alpha),beta));
println("(6)"+ a6.x + "+" + a6.y + "i" );
}
// 2つの複素数の和を計算する関数
PVector c_sum(
PVector c1,
PVector c2
){
PVector sum = c1.copy().add(c2);
return sum;
}
// 2つの複素数の差を計算する関数
PVector c_sub(
PVector c1,
PVector c2
){
PVector sub = c1.copy().sub(c2);
return sub;
}
// 2つの複素数の積を計算する関数
PVector c_prod(
PVector c1,
PVector c2
){
PVector prod = new PVector();
prod.x = c1.x * c2.x - c1.y * c2.y;
prod.y = c1.x * c2.y + c1.y * c2.x;
return prod;
}
// 2つの複素数の商を計算する関数
PVector c_div(
PVector c1,
PVector c2
){
PVector div = new PVector();
div.x = (c1.x * c2.x + c1.y * c2.y)/(c2.x*c2.x+c2.y*c2.y);
div.y = (-c1.x * c2.y + c1.y * c2.x)/(c2.x*c2.x+c2.y*c2.y);
return div;
}ソースコード1 解と係数の関係に関する問題1のプログラム
このソースコード1を、Processingの開発環境ウィンドウを開いて(スケッチ名を「Vietas_formulas1」としています)、テキストエディタ部分に書いて実行すると、図1のように、
(1)0.5+0.0i
(2)0.0+0.0i
(3)-1.0+0.0i
(4)2.5+0.0i
(5)-0.5+0.0i
(6)-1.0+0.0i
とコンソールに出力されます。
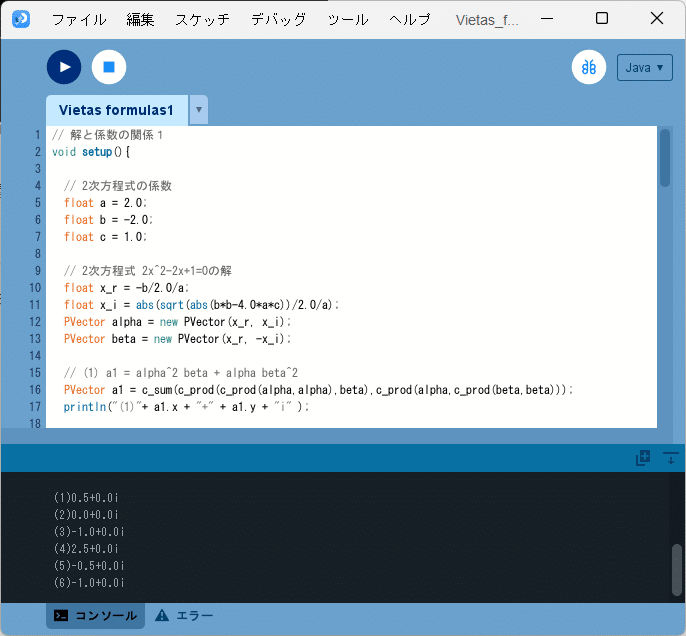
なお、今回の問題の解は虚数部はすべて「0」になりますが、「0」であることを明示するために敢えて表示しました。
解と係数の関係の問題2
2つ目の問題を考えてみます。
問題2
和と積が次のようになる2つの数を求めよ。
(1) 和$${5}$$、積$${-14}$$
(2) 和$${4}$$、積$${-1}$$
(3) 和と積がともに$${2}$$
アルゴリズム設計
この問題は、上記の2次方程式の作成②の性質を利用すれば、2つの数を求める問題を2次方程式の解を求める問題に帰着させることができます。そのため、あとは記事『高校数学をプログラミングで解く(数学II編)「1-2 2次方程式の解と判別式」』で説明した、2次方程式の解の公式を用いて問題を解くことができます。今回はそのときのプログラムを再利用します。
プログラム
それでは、2つの数を求めるプログラムとして2次方程式の解を求めるプログラムを再利用していきます。ここでは、問題2(1)を例にプログラムを記述します。注意点としては、和$${5}$$、積$${-14}$$に対して、2次方程式$${ax^2+bx+c=0}$$の係数は、それぞれ$${a=1, b=-5, c=-14}$$と設定されることです。
// 2次方程式の解を求める
void setup(){
// 2次方程式ax^2+bx+c=0の係数
float a = 1.0;
float b = -5.0;
float c = -14.0;
// 判別式
float D = b*b-4.0*a*c;
// 2次方程式の解の個数を求め、その解も求める
if( D > 0 ){
float x1, x2;
x1 = (-b + sqrt(D))/2.0/a;
x2 = (-b - sqrt(D))/2.0/a;
print("異なる2つの実数解をもつ: ");
println(x1, x2);
} else if( D == 0 ){
float x1;
x1 = -b/2.0/a;
print("ただ1つの実数解(重解)をもつ: ");
println(x1);
} else {
float x_r, x_i;
x_r = -b/2.0/a;
x_i = sqrt(-D)/2.0/a;
print("異なる2つの虚数解をもつ: ");
println(x_r + "+" + abs(x_i) + "i",x_r + "-" + abs(x_i) + "i");
}
}ソースコード2 解の公式による2次方程式の解を求めるプログラム(再掲)
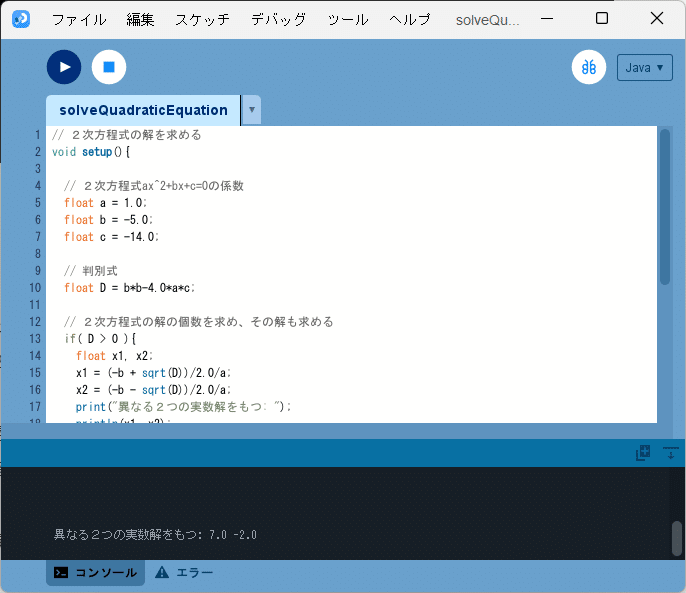
ソースコード2は、記事『高校数学をプログラミングで解く(数学II編)「1-2 2次方程式の解と判別式」』で作成したスケッチ「solveQuadraticEquation」を2次方程式の係数の値を問題2(1)に合わせて調整しただけです。このスケッチ「solveQuadraticEquation」を実行すると、図2のように、
異なる2つの実数解をもつ: 7.0 -2.0
とコンソールに出力され、求めたい2つの数は$${7}$$と$${-2}$$になることがわかります。
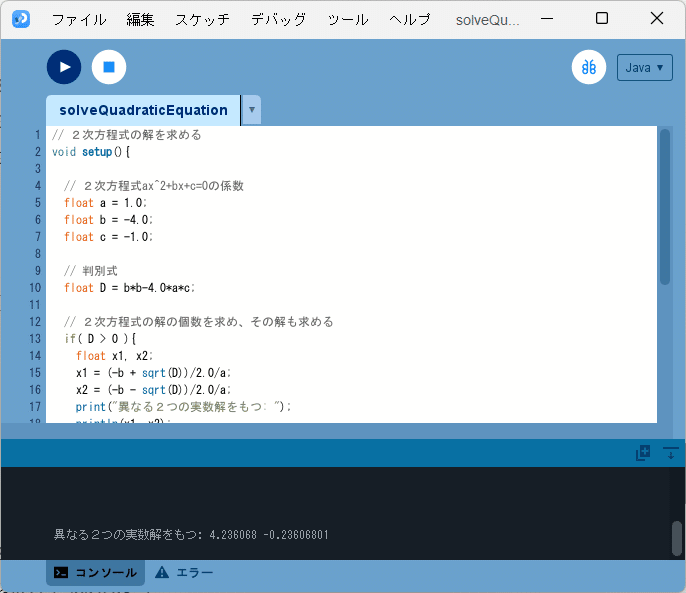
同様にして、問題2(2)や(3)も2次方程式の解を求めるプログラムを利用して2つの数を求めることができます。結果として、問題2(2)はソースコード2に対して$${b=-4, c=-1}$$と設定することで、図3のように、
異なる2つの実数解をもつ: 4.236068 -0.23606801
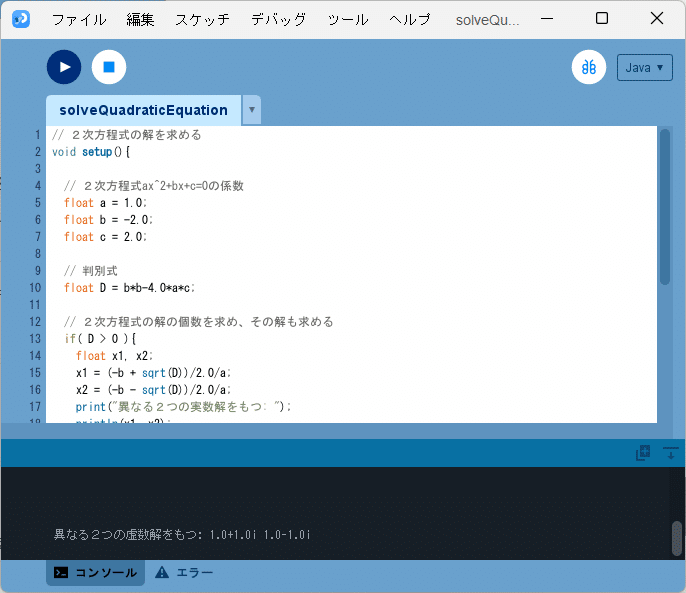
とコンソールに出力されるので、2つの数は$${4.236068 = 2+\sqrt{5}, \ -0.23606801 = 2-\sqrt{5}}$$であることがわかり、問題2(3)はソースコード2に対して$${b=-2, c=2}$$と設定することで、図4のように、
異なる2つの虚数解をもつ: 1.0+1.0i 1.0-1.0i
とコンソールに出力されるので、2つの数は$${1+i, \ 1-i}$$であることがわかります。
解と係数の関係の問題3
最後に、3つ目の問題を考えてみます。
問題3
2次方程式$${(x-1)(x-2)+(x-2)(x-3)+(x-3)(x-1)=0}$$の2つの解を$${\alpha, \beta}$$とするとき、次の式の値を求めよ。
(1) $${\alpha \beta}$$
(2) $${(1-\alpha)(1-\beta)}$$
(3) $${(\alpha-2)(\beta-2)}$$
アルゴリズム設計
この問題は、解と係数の関係から、
$$
\begin{array}{ll}
f(x) &= (x-1)(x-2)+(x-2)(x-3)+(x-3)(x-1) \\
&=3 (x-\alpha)(x-\beta)
\end{array}
$$
という関係が成り立つことに気付けば簡単です(3つ目の式の係数に「3」がつくことを忘れないように注意してください)。つまり、
(1) $${\alpha \beta = (0-\alpha)(0-\beta) = f(0)/3}$$
(2) $${(1-\alpha)(1-\beta) = f(1)/3}$$
(3) $${(\alpha-2)(\beta-2) = (2-\alpha)(2-\beta) = f(2)/3}$$
で計算することができます。
プログラム
では、これらの関係式を利用して問題3の式の値を求めるプログラムを作成していきます。
// 解と係数の関係3
void setup(){
// (1) αβ
float f1 = quadraticfunction(0.0)/3.0;
println("(1) αβ=", f1 );
// (2) (1-α)(1-β)
float f2 = quadraticfunction(1.0)/3.0;
println("(2) (1-α)(1-β)=", f2 );
// (3) (α-2)(β-2)
float f3 = quadraticfunction(2.0)/3.0;
println("(3) (α-2)(β-2)=", f3 );
}
// 2次関数f(x)=(x-1)(x-2)+(x-2)(x-3)+(x-3)(x-1)
float quadraticfunction(
float x
){
return (x-1.0)*(x-2.0)+(x-2.0)*(x-3.0)+(x-3.0)*(x-1.0);
}ソースコード3 問題3の式の値を求めるプログラム
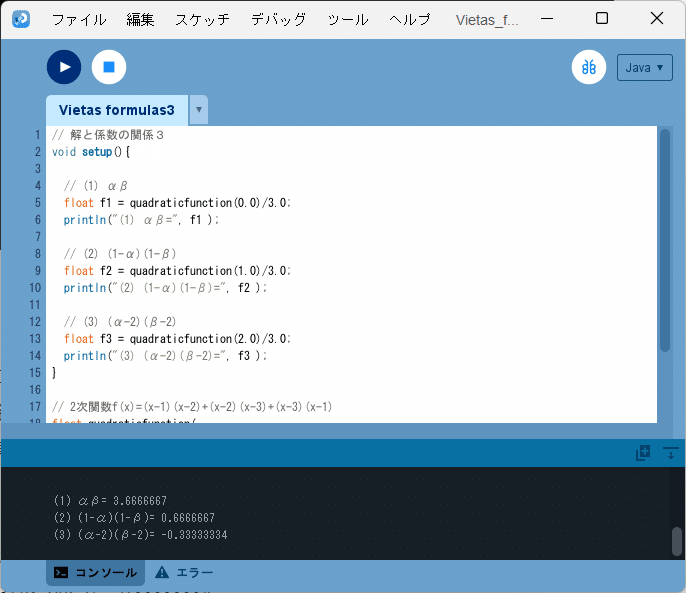
このソースコード3を、Processingの開発環境ウィンドウを開いて(スケッチ名を「Vietas_formulas3」としています)、テキストエディタ部分に書いて実行すると、図5のように、
(1) αβ= 3.6666667
(2) (1-α)(1-β)= 0.6666667
(3) (α-2)(β-2)= -0.33333334
とコンソールに表示されます。
まとめ
今回は、数学IIで学ぶ「解と係数の関係」について、2次方程式の解と係数の関係に関連する3つの問題をプログラミングして解いてみました。
問題1は、解と係数の関係を利用すると簡単に解ける問題ですが、あえて2次方程式の解を求めてそれらを各式に代入して値を求めてみました。
問題2は、2次方程式の作成②の性質を利用して問題を2次方程式を解く問題に帰着させることで比較的簡単に計算することができました。
問題3は、まさに2次方程式の解と係数の関係を式で表すことで、各式の値の計算は非常に簡単になりました。
プログラミングを行う場合、計算自体はコンピュータがやってくれるので、2次方程式の解と係数の関係のような公式を利用してもしなくてもどちらでもよいのですが、コードはやはり公式などを利用した方が簡単になったり、見やすくなったりしますし、コンピュータでの処理自体も速くなることが多いです。そのため、プログラミングでは、できるだけ公式などをうまく使っていくことが重要になってきます。このような書き方にも少しずつ慣れていってください。
参考文献
改訂版 教科書傍用 スタンダード 数学II(数研出版、ISBN9784410209369)
