見出し画像

高校数学をプログラミングで解く（数学I編）「2-5 三角形の面積、空間図形への応用」

MK's papa

はじめに

今回は、数学Iで学ぶ「三角形の面積、空間図形への応用」について、三角形の面積を求める式やヘロンの公式を関数化した後、それらの関数を応用して空間図形の問題をプログラミングして解いてみます。

三角形の面積、ヘロンの公式

まず、三角形の面積を求める方法やヘロンの公式をまとめておきます。△ABCを図1のように設定します。

図1　△ABCの設定

三角形の2辺の長さとその間の角の大きさがわかっている場合

この場合の△ABCの面積$${S}$$は、

$$
S = \frac{1}{2} bc \sin A = \frac{1}{2} ca \sin B = \frac{1}{2} ab \sin C
$$

で計算することができます。

三角形の3辺の長さがわかっている場合（ヘロンの公式）

この場合の△ABCの面積$${S}$$は、

$$
S = \sqrt{s(s-a)(s-b)(s-c)} \ \ \mathrm{ただし} s = \frac{a+b+c}{2}
$$

で計算することができます。なお、この式をヘロンの公式と呼びます。

三角形の面積を求めるための関数

上記2つの三角形の面積を求める式を関数化し、その関数を利用して以下の三角形（図2）の面積を求めていきます。

図2　テスト用の三角形

なお、図2の三角形は45°、45°、90°の直角三角形と30°、60°、90°の直角三角形を組み合わせたものですので、その面積$${S}$$は、

$$
S = \frac{1+\sqrt{3}}{2} =1.3660254\cdots
$$

となります。

三角形の2辺の長さとその間の角の大きさがわかっている場合

この場合に、三角形の面積を求める関数は以下のように表わすことができます。

// 三角形の2辺の長さとその間の角の大きさがわかっている場合に
// 三角形の面積を求める関数
float getArea(
  float side1, // 辺1の長さ
  float side2, // 辺2の長さ
  float angle // 間の角の大きさ（°）
){
  float S = side1 * side2 * sin( radians(angle) ) / 2.0;
  return S;
}

ソースコード1　2辺と間の角がわかっている場合の面積を求める関数

この関数を利用して、図2の三角形の面積を求めるプログラムを作成します。

// 三角形の2辺の長さとその間の角の大きさがわかっている場合に
// 三角形の面積を求める
void setup(){

  // 三角形の辺の長さ
  float a, b, c; 
  a = 2.0;
  b = sqrt(2.0);
  c = 1.0 + sqrt(3.0);

  // 三角形の内角の大きさ
  float A, B, C;
  A = 45.0;
  B = 30.0;
  C = 105.0;

  // 三角形の面積を求める
  float S = getArea( b, c, A );  
  println(S);
  
}

// 三角形の2辺の長さとその間の角の大きさがわかっている場合に
// 三角形の面積を求める関数
float getArea(
  float side1, // 辺1の長さ
  float side2, // 辺2の長さ
  float angle // 間の角の大きさ（°）
){
  float S = side1 * side2 * sin( radians(angle) ) / 2.0;
  return S;
}

ソースコード2　図2の三角形の面積を求めるプログラム（2辺と間の角を利用）

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「getTriangleArea」としています）、テキストエディタ部分に書いて実行すると、図3のように三角形の面積「1.3660253」がコンソールに出力されます。これは、丸め誤差の範囲で真値「1.3660254$${\cdots}$$」と一致しています。

図3　スケッチ「getTriangleArea」の実行結果

三角形の3辺の長さがわかっている場合（ヘロンの公式）

この場合に、三角形の面積を求める関数（ヘロンの公式）は以下のように表わすことができます。

// ヘロンの公式
float heronsformula(
  float side1, // 辺1の長さ
  float side2, // 辺2の長さ
  float side3  // 辺3の長さ
){
  float s = (side1 + side2 + side3)/2.0;
  float S = sqrt( s * (s - side1) * (s - side2) * (s - side3) );
  return S;
}

ソースコード3　ヘロンの公式の関数

この関数を利用して、図2の三角形の面積を求めるプログラムを作成します。

// 三角形の3辺の長さがわかっている場合に三角形の面積を求める
// （ヘロンの公式）
void setup(){

  // 三角形の辺の長さ
  float a, b, c; 
  a = 2.0;
  b = sqrt(2.0);
  c = 1.0 + sqrt(3.0);

  // 三角形の面積を求める
  float S = heronsformula( a, b, c );  
  println(S);
  
}

// ヘロンの公式
float heronsformula(
  float side1, // 辺1の長さ
  float side2, // 辺2の長さ
  float side3  // 辺3の長さ
){
  float s = (side1 + side2 + side3)/2.0;
  float S = sqrt( s * (s - side1) * (s - side2) * (s - side3) );
  return S;
}

ソースコード4　図2の三角形の面積を求めるプログラム（ヘロンの公式を利用）

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「getTriangleArea2」としています）、テキストエディタ部分に書いて実行すると、図4のように三角形の面積「1.3660256」がコンソールに出力されます。これも、丸め誤差の範囲で真値「1.3660254$${\cdots}$$」と一致しています。

図4　スケッチ「getTriangleArea2」の実行結果

空間図形への応用

最後に、ヘロンの公式の空間図形への応用を考えます。
次のような問題を考えます。

問題
$${AB=a=\sqrt{2}, \ AD=b=1, \ AE=c=\sqrt{3}}$$の直方体ABCD-EFGHがあるとき、頂点Aから平面BDEへ下ろした垂線の長さを求めよ。

図5　直方体ABCD-EFGH

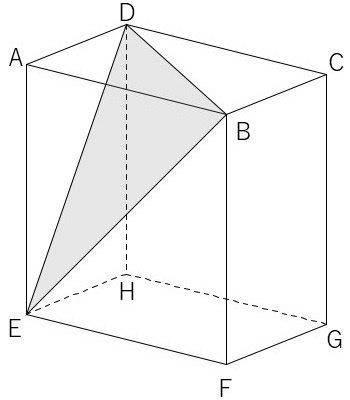
垂線の長さの導出（アルゴルズム設計）

それでは、垂線の長さを求める手順をまとめます。
① 四面体ABDEの体積$${V}$$を求めます。△ABDを四面体ABDEの底面、辺AEを四面体の高さと考えると、

$$
V = \frac{1}{3} \cdot \frac{1}{2}ab \cdot c = \frac{abc}{6}
$$

と計算できます。
② △BDEの面積$${S}$$を求めます。直角三角形ABDに対して三平方の定理を利用すると、

$$
BD = \sqrt{a^2+b^2}
$$

と求めることができます。同様にして、△ADEと△AEBからそれぞれ、

$$
DE = \sqrt{b^2+c^2}, \ EB = \sqrt{c^2+a^2}
$$

が得られます。△BDEの３辺の長さがわかったので、あとはヘロンの公式を用いて、△BDEの面積$${S}$$を求めることができます。
③ 垂線の長さ$${d}$$を求めます。四面体ABDEの体積$${V}$$は△BDEの面積$${S}$$と垂線の長さ$${d}$$とで、

$$
V=\frac{1}{3} Sd
$$

と表すことができるので、垂線の長さ$${d}$$は、

$$
d = \frac{3V}{S}
$$

で求めることができます。

垂線の長さを求めるプログラム

垂線の長さの導出方法はわかったので、垂線の長さを求めるプログラムを作成します。

// 垂線の長さを求める
void setup(){

  // 直方体ABCD-EFGHの３辺の長さ
  float a, b, c; 
  a = sqrt(2.0); // 辺ABの長さ
  b = 1.0;       // 辺ADの長さ
  c = sqrt(3.0); // 辺AEの長さ

  // 四面体ABDEの体積を求める
  float V = a * b * c / 6.0;
  
  // △BDEの３辺の長さを求める
  float BD = sqrt(a*a + b*b);
  float DE = sqrt(b*b + c*c);
  float EB = sqrt(c*c + a*a);
  // △BDEの面積を求める
  float S = heronsformula( BD, DE, EB );
  
  // 頂点Aから平面BDEに下ろした垂線の長さ
  float d = 3.0 * V / S;
  
  println(d);
  
}

// ヘロンの公式
float heronsformula(
  float side1, // 辺1の長さ
  float side2, // 辺2の長さ
  float side3  // 辺3の長さ
){
  float s = (side1 + side2 + side3)/2.0;
  float S = sqrt( s * (s - side1) * (s - side2) * (s - side3) );
  return S;
}

ソースコード5　垂線の長さを求めるプログラム

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「lengthPerpendicular」としています）、テキストエディタ部分に書いて実行すると、図6のように垂線の長さ「0.738549」がコンソールに出力されます。これは、真値

$$
\frac{\sqrt{66}}{11}=0.7385489 \cdots
$$

とほぼ一致しています。

図6　スケッチ「lengthPerpendicular」の実行結果


まとめ

今回は、数学Iで学ぶ「三角形の面積、空間図形への応用」について、三角形の面積を求める式やヘロンの公式を関数化した後、それらの関数を応用して空間図形の問題をプログラミングして解いてみました。
今回のように、三角形の面積を求める式やヘロンの公式のような汎用的に使える公式などを関数化しておくことはプログラミングでよく利用されますので、少しずつ慣れていってください。
また、プログラミングでは、様々な値を一度変数に入れてから使うということが常識的になされています。例えば、ソースコード5では、最初に

a = sqrt(2.0); // 辺ABの長さ

と変数aを初期化しています。この初期化以降、$${\sqrt{2}}$$という値を直接利用することはなく、変数aを通して利用しています。このような変数の利用方法はプログラミングする際の作法としてぜひ覚えておいてください。

参考文献

改訂版 教科書傍用 スタンダード 数学I（数研出版、ISBN9784410209178）

この記事が気に入ったらサポートをしてみませんか？