
高校数学をプログラミングで解く(数学I編)「2-2 三角比の相互関係」
はじめに
今回は、数学Iで学ぶ「三角比の相互関係」について、三角形の相互関係を表す式や$${90^{\circ}-\theta}$$の三角比を表す式が成り立っているのかを確かめるプログラムを作成します。
三角比の相互関係
まず、三角比の相互関係の式や$${90^{\circ}-\theta}$$の三角比の式をまとめておきます。
三角比の相互関係
$$
\tan \theta = \frac{ \sin \theta}{ \cos \theta }
$$
$$
\sin^2 \theta + \cos^2 \theta = 1
$$
$$
1+\tan^2 \theta = \frac{1}{\cos^2 \theta}
$$
$${90^{\circ}-\theta}$$の三角比
$$
\sin ( 90^{\circ}-\theta ) = \cos \theta
$$
$$
\cos ( 90^{\circ}-\theta ) = \sin \theta
$$
$$
\tan ( 90^{\circ}-\theta ) = \frac{1}{\tan \theta}
$$
今回は、これらの式が成り立っていることをプログラムを書いて確かめてみます。具体的には、$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつ動かしていき、左辺の値と右辺の値をそれぞれ出力することで一致しているかどうか確かめることができるようにします。
三角比の相互関係を確かめる
では、順にプログラムを書いて確かめていきます。
三角比の相互関係1
まず、
$$
\tan \theta = \frac{ \sin \theta}{ \cos \theta }
$$
を見ていきます。
void setup(){
float theta; // 角度(°)
float lhs, rhs; // 左辺と右辺の値
for(int i=1; i<=8; i++){ // 10°から80°まで動かす
theta = 10.0 * i;
lhs = tan( radians(theta) );
rhs = sin( radians(theta) )/cos( radians(theta) );
println( theta, lhs, rhs );
}
}ソースコード1 三角比の相互関係(1つ目)を確かめるプログラム
ソースコード1を、Processingの開発環境ウィンドウを開いて(スケッチ名を「relation_trigonometric_ratio1」としています)、テキストエディタ部分に書いて実行します。

図1のように、コンソールに角度($${\theta}$$)の値(単位は「°」)、左辺($${\tan \theta}$$)の値、右辺($${\sin \theta / \cos \theta}$$)の値、の順で$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で出力しています。出力された値を以下に書き出してみます。
10.0 0.17632698 0.17632699
20.0 0.36397022 0.36397022
30.0 0.57735026 0.57735026
40.0 0.8390996 0.8390996
50.0 1.1917536 1.1917535
60.0 1.7320509 1.732051
70.0 2.7474773 2.7474773
80.0 5.6712804 5.6712804
この結果を見ると、左辺の値と右辺の値は丸め誤差の範囲内で一致していることがわかります。つまり、
$$
\tan \theta = \frac{ \sin \theta}{ \cos \theta }
$$
は成り立っているだろうということが確認できます。
三角比の相互関係2
次に、
$$
\sin^2 \theta + \cos^2 \theta = 1
$$
を見ていきます。
// 三角比の相互関係 sin^2θ+cos^2θ=1 の確認
void setup(){
float theta; // 角度(°)
float lhs; // 左辺の値
for(int i=1; i<=8; i++){ // 10°から80°まで動かす
theta = 10.0 * i;
lhs = sin( radians(theta) ) * sin( radians(theta) );
lhs += cos( radians(theta) ) * cos( radians(theta) );
println( theta, lhs );
}
}ソースコード2 三角比の相互関係(2つ目)を確かめるプログラム
ソースコード2を、Processingの開発環境ウィンドウを開いて(スケッチ名を「relation_trigonometric_ratio2」としています)、テキストエディタ部分に書いて実行します。
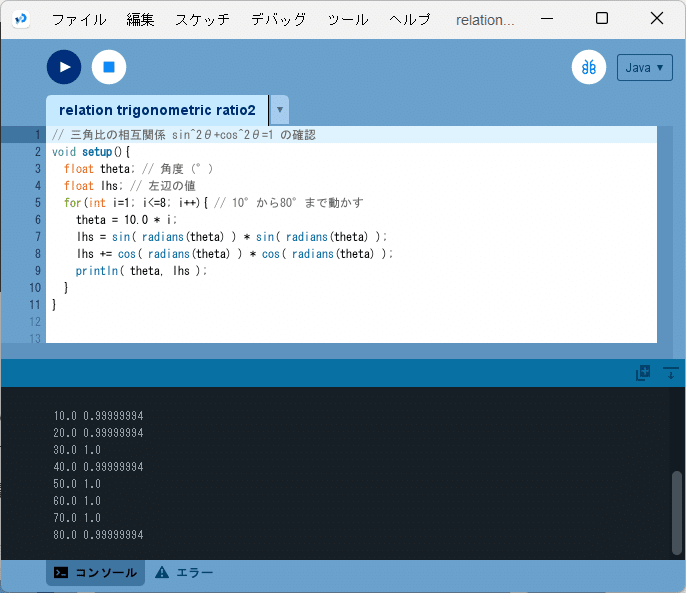
図2のように、コンソールに角度($${\theta}$$)の値(単位は「°」)、左辺($${\sin^2 \theta + \cos^2 \theta}$$)の値、の順で$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で出力しています。なお、右辺の値は常に1であるため、出力は省略しています。出力された値を以下に書き出してみます。
10.0 0.99999994
20.0 0.99999994
30.0 1.0
40.0 0.99999994
50.0 1.0
60.0 1.0
70.0 1.0
80.0 0.99999994
この結果を見ると、左辺の値は丸め誤差の範囲内で「1」と一致していることがわかります。つまり、
$$
\sin^2 \theta + \cos^2 \theta = 1
$$
は成り立っているだろうということが確認できます。
三角比の相互関係3
今度は、
$$
1+\tan^2 \theta = \frac{1}{\cos^2 \theta}
$$
を見ていきます。
// 三角比の相互関係 1+tan^2θ=1/cos^2θ の確認
void setup(){
float theta; // 角度(°)
float lhs, rhs; // 左辺と右辺の値
for(int i=1; i<=8; i++){ // 10°から80°まで動かす
theta = 10.0 * i;
lhs = 1.0 + tan( radians(theta) ) * tan( radians(theta) );
rhs = 1.0 / cos( radians(theta) ) / cos( radians(theta) );
println( theta, lhs, rhs );
}
}ソースコード3 三角比の相互関係(3つ目)を確かめるプログラム
ソースコード3を、Processingの開発環境ウィンドウを開いて(スケッチ名を「relation_trigonometric_ratio3」としています)、テキストエディタ部分に書いて実行します。

図3のように、コンソールに角度($${\theta}$$)の値(単位は「°」)、左辺($${1 + \tan^2 \theta}$$)の値、右辺($${1 / \cos^2 \theta}$$)の値、の順で$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で出力しています。出力された値を以下に書き出してみます。
10.0 1.0310912 1.0310912
20.0 1.1324743 1.1324743
30.0 1.3333333 1.3333334
40.0 1.7040881 1.7040882
50.0 2.4202766 2.4202764
60.0 4.0 4.000001
70.0 8.548632 8.548632
80.0 33.16342 33.16342
この結果を見ると、左辺の値と右辺の値は丸め誤差の範囲内で一致していることがわかります。つまり、
$$
1+\tan^2 \theta = \frac{1}{\cos^2 \theta}
$$
は成り立っているだろうということが確認できます。
90°ーθの三角比を確かめる
今度は、$${90^{\circ}-\theta}$$の三角比をプログラムを書いて確かめていきます。
90°ーθの三角比1
1つ目の
$$
\sin ( 90^{\circ}-\theta ) = \cos \theta
$$
を見ていきます。
// 90°-θの三角比 sin(90°-θ)=cosθ の確認
void setup(){
float theta; // 角度(°)
float lhs, rhs; // 左辺と右辺の値
for(int i=1; i<=8; i++){ // 10°から80°まで動かす
theta = 10.0 * i;
lhs = sin( radians(90.0 - theta) );
rhs = cos( radians(theta) );
println( theta, lhs, rhs );
}
}ソースコード4 $${90^{\circ}-\theta}$$の三角比(1つ目)を確かめるプログラム
ソースコード4を、Processingの開発環境ウィンドウを開いて(スケッチ名を「minus90_trigonometric_ratio1」としています)、テキストエディタ部分に書いて実行します。

図4のように、コンソールに角度($${\theta}$$)の値(単位は「°」)、左辺($${\sin ( 90^{\circ}-\theta)}$$)の値、右辺($${\cos \theta}$$)の値、の順で$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で出力しています。出力された値を以下に書き出してみます。
10.0 0.9848077 0.9848077
20.0 0.9396926 0.9396926
30.0 0.86602545 0.8660254
40.0 0.76604444 0.76604444
50.0 0.6427876 0.64278764
60.0 0.5 0.49999997
70.0 0.34202012 0.34202015
80.0 0.17364818 0.17364822
この結果を見ると、左辺の値と右辺の値は丸め誤差の範囲内で一致していることがわかります。つまり、
$$
\sin ( 90^{\circ}-\theta ) = \cos \theta
$$
は成り立っているだろうということが確認できます。
90°ーθの三角比2
2つ目の
$$
\cos ( 90^{\circ}-\theta ) = \sin \theta
$$
を見ていきます。
// 90°-θの三角比 cos(90°-θ)=sinθ の確認
void setup(){
float theta; // 角度(°)
float lhs, rhs; // 左辺と右辺の値
for(int i=1; i<=8; i++){ // 10°から80°まで動かす
theta = 10.0 * i;
lhs = cos( radians(90.0 - theta) );
rhs = sin( radians(theta) );
println( theta, lhs, rhs );
}
}ソースコード5 $${90^{\circ}-\theta}$$の三角比(2つ目)を確かめるプログラム
ソースコード5を、Processingの開発環境ウィンドウを開いて(スケッチ名を「minus90_trigonometric_ratio2」としています)、テキストエディタ部分に書いて実行します。

図5のように、コンソールに角度($${\theta}$$)の値(単位は「°」)、左辺($${\cos ( 90^{\circ}-\theta)}$$)の値、右辺($${\sin \theta}$$)の値、の順で$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で出力しています。出力された値を以下に書き出してみます。
10.0 0.17364822 0.17364818
20.0 0.34202015 0.34202012
30.0 0.49999997 0.5
40.0 0.64278764 0.6427876
50.0 0.76604444 0.76604444
60.0 0.8660254 0.86602545
70.0 0.9396926 0.9396926
80.0 0.9848077 0.9848077
この結果を見ると、左辺の値と右辺の値は丸め誤差の範囲内で一致していることがわかります。つまり、
$$
\cos ( 90^{\circ}-\theta ) = \sin \theta
$$
は成り立っているだろうということが確認できます。
90°ーθの三角比3
最後に、3つ目の
$$
\tan ( 90^{\circ}-\theta ) = \frac{1}{\tan \theta}
$$
を見ていきます。
// 90°-θの三角比 tan(90°-θ)=1/tanθ の確認
void setup(){
float theta; // 角度(°)
float lhs, rhs; // 左辺と右辺の値
for(int i=1; i<=8; i++){ // 10°から80°まで動かす
theta = 10.0 * i;
lhs = tan( radians(90.0 - theta) );
rhs = 1.0 / tan( radians(theta) );
println( theta, lhs, rhs );
}
}ソースコード6 $${90^{\circ}-\theta}$$の三角比(3つ目)を確かめるプログラム
ソースコード6を、Processingの開発環境ウィンドウを開いて(スケッチ名を「minus90_trigonometric_ratio3」としています)、テキストエディタ部分に書いて実行します。

図6のように、コンソールに角度($${\theta}$$)の値(単位は「°」)、左辺($${\tan ( 90^{\circ}-\theta)}$$)の値、右辺($${1/\tan \theta}$$)の値、の順で$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で出力しています。出力された値を以下に書き出してみます。
10.0 5.6712804 5.671282
20.0 2.7474773 2.7474775
30.0 1.7320509 1.7320509
40.0 1.1917536 1.1917536
50.0 0.8390996 0.8390996
60.0 0.57735026 0.57735026
70.0 0.36397022 0.36397025
80.0 0.17632698 0.17632702
この結果を見ると、左辺の値と右辺の値は丸め誤差の範囲内で一致していることがわかります。つまり、
$$
\tan ( 90^{\circ}-\theta ) = \frac{1}{\tan \theta}
$$
は成り立っているだろうということが確認できます。
まとめ
今回は、数学Iで学ぶ「三角比の相互関係」について、三角形の相互関係を表す式や$${90^{\circ}-\theta}$$の三角比を表す式が成り立っているのかを確かめるプログラムを作成しました。
各節の最後で「成り立っているだろうということが確認できます。」としました。これは、今回プログラムを書いて各式が成り立っていることを証明したわけではなく、単に成り立っていそうであることを確かめただけだからです。つまり、$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で式が成り立っていることを確かめましたが、例えば、$${\theta=11^{\circ}}$$で式が成り立つかどうかは計算してみないとわからないということです。というわけで、「成り立っているだろう」としています。
なお、今回の各式を証明することはそんなに難しくありません。直角三角形を用いた三角比の定義を用いることで簡単に証明することができます。一度、これらの式を証明しておくことをお勧めします。
参考文献
改訂版 教科書傍用 スタンダード 数学I(数研出版、ISBN9784410209178)
この記事が気に入ったらサポートをしてみませんか?
