
高校数学10分プログラミング(数学B編 1.平面上のベクトル)4日目「ベクトルと図形の性質を考える」
マガジンリスト > 数学B編 1.平面上のベクトル > 4日目 課題
おはようございます。
本日は、高校数学10分プログラミング(数学B編 1.平面上のベクトル)の4日目です。
本日の課題は、ベクトルと図形に関する性質の応用例として、三角形の内心の位置ベクトルを計算して、座標上に描くプログラムを作成することです。
ベクトルと図形に関する性質
まず、ベクトルと図形に関する性質についてまとめておきます。
一直線上の3点
2点$${\mathrm{A, B}}$$が異なるとき
点$${\mathrm{P}}$$が直線$${\mathrm{AB}}$$上にある $${ \Leftrightarrow }$$ $${ \overrightarrow{ \mathrm{AP} } = k \overrightarrow{ \mathrm{AB} } }$$となる実数$${k}$$がある
ベクトルの相等
$${ s, t, s', t' }$$は実数とする。
$${ \vec{a} \neq \vec{0}, \ \vec{b} \neq \vec{0}, \ \vec{a} / \!\! / \!\!\!\!\! \backslash \vec{b} }$$のとき、
$$
s \vec{a} + t \vec{b} = s' \vec{a} + t' \vec{b} \Leftrightarrow s = s', \ t = t'
$$
特に
$$
s \vec{a} + t \vec{b} = \vec{0} \Leftrightarrow s=t=0
$$
課題
平面上の3点$${\mathrm{A}(\vec{a}=(1,1))}$$、$${\mathrm{B}(\vec{b}=(7,1))}$$、$${\mathrm{C}(\vec{c}=(3,5))}$$を頂点とする$${ \triangle \mathrm{ABC}}$$に、その内心$${\mathrm{I}}$$の位置ベクトル$${\vec{i}}$$を描くプログラムを作成してください。
ヒント
三角形の内心は「3つの内角の二等分線が交わる点」となります(図1)。
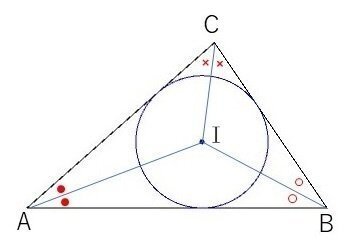
三角形の内心はその三角形の内接円の中心となります。
そして、内心の位置ベクトル$${\vec{i}}$$は、$${ \triangle \mathrm{ABC}}$$の頂点の位置ベクトル$${ \vec{a}, \ \vec{b}, \ \vec{c} }$$を用いて、
$$
\vec{i} = \frac{1}{p} \left( \left|\vec{c}-\vec{b} \right| \vec{a}+\left|\vec{a}-\vec{c} \right| \vec{b}+\left|\vec{b}-\vec{a} \right| \vec{c} \right)
$$
と表すことができます。ここで、$${p}$$は$${ \triangle \mathrm{ABC}}$$の周囲の長さを表し、
$$
p=\left|\vec{b}-\vec{a} \right|+\left|\vec{c}-\vec{b} \right|+\left|\vec{a}-\vec{c} \right|
$$
で与えられます。
プログラム
今回の課題の内心$${\mathrm{I}}$$の位置ベクトル$${\vec{i}}$$を描くためのスケッチ「drawPositionVectorofInnerCenter」を準備しました。以下の zip ファイルをダウンロードして展開または解凍してご利用ください。
展開または解凍して得られるスケッチ「drawPositionVectorofInnerCenter」の中のpdeファイル「drawPositionVectorofInnerCenter.pde」をダブルクリックしてスケッチ「drawPositionVectorofInnerCenter」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawPositionVectorofInnerCenter」タブを選択すると、そのテキストエリアに以下のソースコードが書かれています。
// 三角形の内心の位置ベクトルを描く
void setup(){
size(500,500,P2D);
noLoop();
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
setAxes(x_range, y_range); // 座標軸の準備
// △ABCの頂点の位置ベクトル
PVector a = new PVector(1.0, 1.0);
PVector b = new PVector(7.0, 1.0);
PVector c = new PVector(3.0, 5.0);
// 三角形ABCの各辺の長さ
float AB_length = ;
float BC_length = ;
float CA_length = ;
// 三角形の周囲の長さ
float perimeter = ;
// 内心の位置ベクトル
PVector i =
// 以下に図形を描いていく
noFill(); // 図形の中身を塗りつぶさない
// △ABCを描く
stroke(128,128,128);
triangle(
a.x * width / 2.0 / x_range, a.y * width / 2.0 / x_range,
b.x * width / 2.0 / x_range, b.y * width / 2.0 / x_range,
c.x * width / 2.0 / x_range, c.y * width / 2.0 / x_range
);
// 三角形の頂点の位置ベクトルの色を黒色に設定
stroke(0,0,0);
// キャンバスにベクトルを描画
arrow(0.0, 0.0, a.x, a.y, x_range);
arrow(0.0, 0.0, b.x, b.y, x_range);
arrow(0.0, 0.0, c.x, c.y, x_range);
// 内心の位置ベクトルを赤色に設定
stroke(255,0,0);
arrow(0.0, 0.0, i.x, i.y, x_range);
}ソースコード1 $${ \triangle \mathrm{ABC}}$$に、その内心$${\mathrm{I}}$$の位置ベクトル$${\vec{i}}$$を描くプログラム(未完成)
このソースコード1の、$${ \triangle \mathrm{ABC}}$$の各辺の長さを与える部分
// 三角形ABCの各辺の長さ
float AB_length = ;
float BC_length = ;
float CA_length = ;や、三角形の周囲の長さを与える部分
// 三角形の周囲の長さ
float perimeter = ;そして、内心の位置ベクトル$${\vec{i}}$$を与える部分
// 内心の位置ベクトル
PVector i = は未完成です。ヒントで与えた式を参考に、未完成の部分に追記して、プログラムを完成させてください。
それでは、よろしくお願いします。
MK's papa
