
相関と見せかけの相関の違いを考える
最近、会社のデータの関係性を分析しようと思っていて、相関、因果などを調べているのですが、その中で勉強したこと、考えたこと、学んだことを一回まとめてみたいと思います。
相関とは
まずは、一番の基礎となる相関からスタート。相関とはなにか。英語の方が考えやすいと感じているのですが、英語では、correlation(統計の関数などではcor とかcorrみたいな関数になることが多いですよね)。きっと co-relationなんです。つまり、お互いに関係している状態ということです。
もう少し具体的に見ていきましょう。二つの変数、AとBがあるとき、二つの変数が関係しているとはどういうことでしょうか。
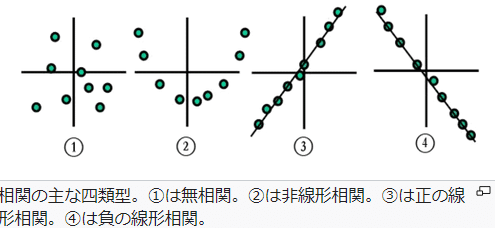
下のグラフの②~④が関係性を持っている状態です。でも②はあまり使われることがなく、一般的には③、④をイメージする人が多いと思います。
Aが大きくなった時にBが大きくなったり、小さくなったり。その動き方の共通性を相関と呼び、その大きさを相関係数という-1~1の間の数字としてわかりやすく計算します。絶対値が1に近いほうが相関が強いということになります。
2種類のデータをそれぞれ縦軸横軸にマッピングして関係性を見る。時間軸に合わせて2種類のグラフを重ねてみる。このあたりはどちらもデータの相関を見ていることになります。
ちなみに、この相関係数については、0.7以上あればとか0.8以上あれば相関が強いというとかありますが、そこは相対的な部分もあるということのようです。
ちなみに、上のグラフの③、④の場合、相関係数は外側の大きな外れ値に非常に影響を受けやすいという性質があるので、そこは要注意。(具体例いれたい。)端の点を外すと相関係数が急に下がることがあるので、ただ相関係数を見るだけではなく、どういう散布図なのかを見るのが重要なようです。
相関でよく聞く話その2。相関は因果じゃないという話。
もう少し正確に言うと、因果は相関の中の一部であり、相関があるからと言って因果が必ずしもあるわけではないということです。
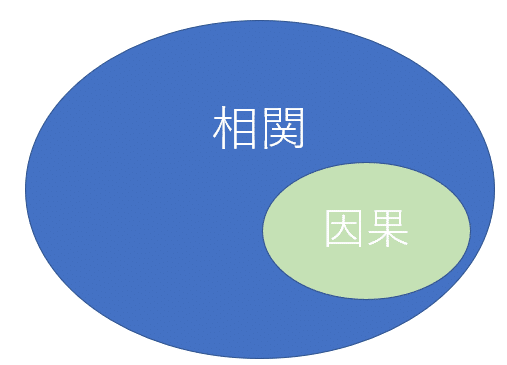
因果というのは二つの変数の関係性に方向性があるというイメージ。
例えば、A→B。Aの影響を受けてBの動きが決まるもので、逆は保証されない関係。 テスト前の勉強時間とテストの点数みたいなものでしょうか?
勉強時間を増やせば増やすほどその人の点数は上がるはずですが、テストの点数が高いからといってその人がすごく勉強したとは限らないというイメージです
見せかけの相関(疑似相関)ってなんだ
さらに、ここに見せかけの相関(疑似相関)と呼ばれるものもあります。
今回のメインのテーマはここです。
変数が3つ出てくる相関関係で
AとBに相関がある状態なのですが、C→A, C→Bの因果関係が成り立っているときに、Cを介してAとBが相関しているという状態です。
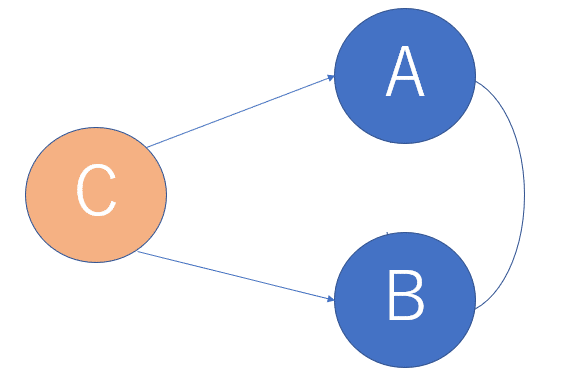
もう少し具体的な例を出してみましょう。
握力と算数の計算力って相関するでしょうか?
数学ではなく、算数としたところが肝だったりするのですが、算数を勉強している。小学生に絞ったら相関するはずなんです。小学1年生は、総じて、握力も計算力も6年生より低い。
握力がA, 計算力がB そして、年齢がCになります。
年齢(正確には、義務教育の年数かな)がA,Bをそれぞれ高くする変数になっており、結果AとBに相関があるように見えます。この年齢である変数Cを統計学的には交絡因子と言ったりします。
それでも、見せかけの相関でも相関があるのは良いことではないかと考えるかもしれません。ただこのときに一番難しいのは、他の要因でAだけ動くことも十分にあり得るため、次も同じように相関してくれるかわからない点です。
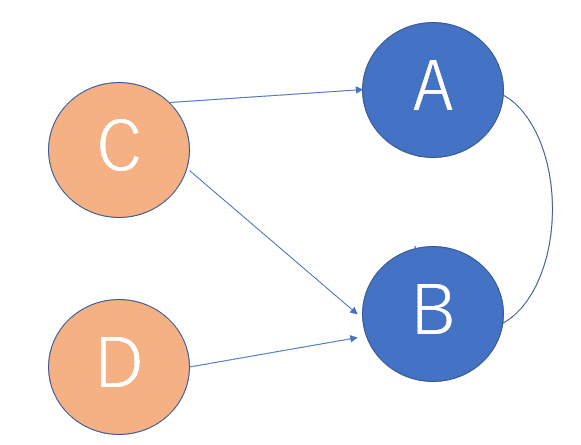
上の図をイメージして、握力と算数の計算力ようなケースをアップデートして考えてみましょう。先ほどと同じようにAが握力、Bが算数の計算力、Cが年齢に、Dとして低年齢からできる面白すぎる教材(すごいYoutuberとか、ゲームとかですね)みたいなものが急に登場すると、Bの算数の計算力は上がります。ただこのとき、AとBに直接の関係がないため、本来Aは変わりません。
このように直接関係がない場合、片方が増加したときにもう片方が一緒に上がってくれる可能性はありますが、上がらない可能性も十分にあるというのが見せかけの相関かどうかを意識しなくてはならないポイントになります。
じゃぁどうすればよいのか(実験計画 or 重回帰分析 (偏相関))
では、交絡因子とよばれる二つの変数に関連する変数の影響を除いてAとBの関係を見るにはどうしたらよいのでしょうか。
先ほどの例で考えるとわかりやすいかもしれません。
同じ学年の中で、握力と計算力に相関があるのかどうかを見てみるとよいはずです。おそらく、相関はないか、弱い負の相関になることもあるかもしれません。
このように、見せかけの相関かどうかを知るためには、交絡因子が同じ条件の時に、AとBにどのような関係性があるかを見ることで本当の関係性を見ることができます。
具体的な方法としては、2パターンに分かれると考えています。
1つ目は、条件を均等になるように、比較したいものだけ差をつけるように分けたあとで、その差の部分だけをテストする方法。統計学的には計画実験法というものがフィッシャーという人のアイデアであります。(統計検定でもよく出る3原則というやつです。)現在では、RCTテストと呼ばれるもので、ABテストといわれたりもします。(すべてのABテストがちゃんとRCTテストになっているかといわれると・・・・)。
もう一つは今あるデータから、条件を合わせたときの影響を見る方法で、条件が同じだったときにその相関係数をみる偏相関係数を計算したり、重回帰分析をすることで、ゴールとなる変数への影響を見るときに、他の条件が変わらなかった時の影響を見たりという方法で検証する方法です。
ただ、ここで問題なことが、そもそも交絡因子のデータはとれるのかということです。そのため、本来であれば、ちゃんと実験計画をしてデータを取得したほうが納得のいく結果が得られやすいというイメージです。
年齢のような取得できるものであればよいのですが、雰囲気とかモチベーションみたいなものは定量化することが難しかったり、アンケートのようなもので取得するなど取得にコストがかかるものがあったりします。
また、交絡因子かどうかわからないものもあるので、怪しい変数はできるだけ多く一緒に検証する必要が出てきたりしますが、そうするとお互いの関係を排除しすぎてしまったり、この辺をうまく使う方法をもう少し研究していきたいと思います。
ここまで読んでいただきありがとうございます。 スキを押していただけると嬉しいです。 フォローしていただけるとさらにうれしいです。
