渦なしベクトル場が保存場であることを導く

2023年2月5日 00:14

理系の大学生が学ぶ基礎的な数学の中で、学生が苦手とするものに「ベクトル解析」があります。ベクトル解析は電磁気学や流体力学を学ぶ際には必須となりますが、ベクトルと微積分が組み合わされていて、学生には難解の分野であるようです。使われる記号も $${ \nabla }$$ とか $${ \oint }$$ とか見慣れないものが多数出てきて、理屈は二の次で計算の仕方に習熟するので精一杯、となりがちです。この記事では、ベクトル解析においてすっ飛ばされてしまいがちな部分での「行間を埋める」ことをしていきます。

今回は、3次元ベクトル場 $${ \bm{A} (\bm{x}) }$$ について、以下の 1. 2. 3. が同値であることを説明します:

　恒等的に　 $${ \nabla \times \bm{A} = 0 }$$ 　である
　任意の閉曲線 $${ \mathcal{C} }$$ に対して　 $${ \displaystyle \oint_{\mathcal{C}} \bm{A} \cdot \mathrm{d} \bm{r} = 0 }$$ 　が成り立つ
　$${ \bm{A} = \nabla U }$$ 　となる関数 $${ U }$$ が存在する　（このようなベクトル場 $${ \bm{A} }$$ を保存場といいます）

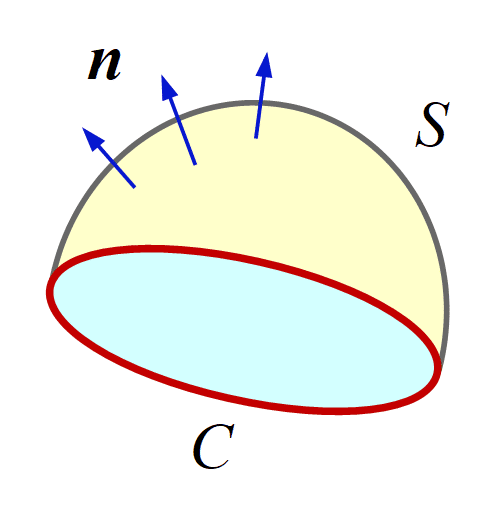
まず押さえておく必要があるのは、ストークスの定理です。閉曲線 $${ \mathcal{C} }$$ を周とする曲面 $${ \mathcal{S} }$$ を考えて、微小面積要素 $${ \mathrm{d} S }$$ での単位法線ベクトルを $${ \bm{n} }$$ とすると、ベクトル場 $${ \bm{A} }$$ について

$$
\iint_{\mathcal{S}} \left( \nabla \times \bm{A} \right) \cdot \bm{n} \mathrm{d} S
= \oint_{\mathcal{C}} \bm{A} \cdot \mathrm{d} \bm{r}
$$

が成り立つ、という定理です。

この定理を前提にすると、1. $${ \Rightarrow }$$ 2. はすぐに分かります。また、3. $${ \Rightarrow }$$ 1. はベクトル解析の基本的な公式から、やはりすぐに分かります。3. $${ \Rightarrow }$$ 2. は、3. $${ \Rightarrow }$$ 1. $${ \Rightarrow }$$ 2. とたどればよいですが、以下のようにして直接示すこともできます:

点 $${ \mathrm{P} }$$ と点 $${ \mathrm{Q} }$$ を結ぶ曲線 $${ \mathcal{C}_{\mathrm{PQ}} }$$ に沿った、点 $${ \mathrm{P} }$$ から点 $${ \mathrm{Q} }$$ までの線積分

$$
\int_{\mathcal{C}_{\mathrm{PQ}}} \bm{A} \cdot \mathrm{d} \bm{r}
$$

を考えます。曲線 $${ \mathcal{C}_{\mathrm{PQ}} }$$ はパラメータ $${ s }$$ によって $${ \bm{x} = \bm{r} (s) }$$ と表され、点 $${ \mathrm{P}, \mathrm{Q} }$$ でそれぞれ $${ s = p, q }$$ であるとします。 $${ \bm{A} = \nabla U }$$ のとき

$$
\int_{\mathcal{C}_{\mathrm{PQ}}} \bm{A} \cdot \mathrm{d} \bm{r} =
\int_{\mathcal{C}_{\mathrm{PQ}}} \nabla U \cdot \mathrm{d} \bm{r} =
\int_{p}^{q}
\left( \frac{\partial U}{\partial x} \frac{\mathrm{d} x}{\mathrm{d} s} +
\frac{\partial U}{\partial y} \frac{\mathrm{d} y}{\mathrm{d} s} +
\frac{\partial U}{\partial z} \frac{\mathrm{d} z}{\mathrm{d} s} \right) \mathrm{d} s \\\ \\
= \int_{p}^{q} \frac{\mathrm{d} U}{\mathrm{d} s} \mathrm{d} s = U (\bm{r} (q)) - U (\bm{r} (p))
$$

となり、この線積分の値は積分経路によらず、始点と終点での $${ U }$$ の値でのみ決まることが分かります。閉曲線を一周する経路の場合は、始点と終点が同じ点ですから、それに沿った線積分はゼロとなります。

このようにして 1. $${ \Rightarrow }$$ 2.,　3. $${ \Rightarrow }$$ 1.,　3. $${ \Rightarrow }$$ 2. は比較的簡単に示すことができますが、2. $${ \Rightarrow }$$ 1. と 2. $${ \Rightarrow }$$ 3. を示すのは少し難しく、工夫が必要です。以下、そのことを解説していきます。

「『閉曲線に沿った線積分がゼロ』ならば『渦なし場』」を示す

まず 2. $${ \Rightarrow }$$ 1. を示すことを考えます。これは直接的に示すのが難しいので、背理法を使います。2. が成り立っているときに、1. が成り立たないとすると矛盾が生じる、ということを示せばよいわけです。そこで、空間内のある領域 $${ \mathcal{D} }$$ で $${ \nabla \times \bm{A} \ne 0 }$$ となっているとします。そして、その領域 $${ \mathcal{D} }$$ 内に曲面 $${ \mathcal{S} }$$ として、「単位法線ベクトル $${ \bm{n} }$$ が $${ \nabla \times \bm{A} }$$ と同じ向きである」つまり $${ \nabla \times \bm{A} = k \bm{n} }$$ （$${ k }$$ は正の定数）となっているようなものを考えます。曲面 $${ \mathcal{S} }$$ の周を $${ \mathcal{C} }$$ とすると、ストークスの定理より

$$
\oint_{\mathcal{C}} \bm{A} \cdot \mathrm{d} \bm{r} =
\iint_{\mathcal{S}} \left( \nabla \times \bm{A} \right) \cdot \bm{n} \mathrm{d} S
= \iint_{\mathcal{S}} k \bm{n} \cdot \bm{n} \mathrm{d} S
$$

となりますが、これは正の値をとる（ゼロにはならない）ので 2. に矛盾します。この矛盾は「空間内のある領域 $${ \mathcal{D} }$$ で $${ \nabla \times \bm{A} \ne 0 }$$ となっている」という仮定をしたことにより生じたものですので、この仮定は成り立たない、つまり「恒等的に $${ \nabla \times \bm{A} = 0 }$$ が成り立つ」ということが言えます。
ポイントは、ストークスの定理で曲面 $${ \mathcal{S} }$$ の選び方は任意なので、もし $${ \nabla \times \bm{A} \ne 0 }$$ の領域があるとすると、その領域において $${ \left( \nabla \times \bm{A} \right) \cdot \bm{n} }$$ を正の値しかとらない（または負の値しかとらない）ような曲面をつくることができてしまう、というところです。

「『閉曲線に沿った線積分がゼロ』ならば『保存場』」を示す

最後に 2. $${ \Rightarrow }$$ 3. を示します。2. が成り立つとき、ある曲線 $${ \mathcal{C} }$$ に沿った線積分

$$
\int_{\mathcal{C}} \bm{A} \cdot \mathrm{d} \bm{r} \qquad (\ast)
$$

の値は積分経路の始点と終点のみで決まり、途中の経路にはよらないことが言えます。なぜなら、ある点 $${ \mathrm{P} }$$ から別の点 $${ \mathrm{Q} }$$ に至る二つの経路 $${ \mathcal{C}_1 , \mathcal{C}_2 }$$ を考えると、点 $${ \mathrm{P} }$$ から $${ \mathcal{C}_1 }$$ を通って点 $${ \mathrm{Q} }$$ まで行った後、$${ \mathcal{C}_2 }$$ を逆向きに通って点 $${ \mathrm{P} }$$ に戻ってくる経路を閉曲線と見なすことにより（この閉曲線を $${ \mathcal{C}_{\mathrm{PQP}} }$$ とします）

$$
\oint_{\mathcal{C}_{\mathrm{PQP}}} \bm{A} \cdot \mathrm{d} \bm{r}
= \int_{\mathcal{C}_1} \bm{A} \cdot \mathrm{d} \bm{r} +
\left( - \int_{\mathcal{C}_2} \bm{A} \cdot \mathrm{d} \bm{r} \right)
$$

であり、これが 2. からゼロなので

$$
\int_{\mathcal{C}_1} \bm{A} \cdot \mathrm{d} \bm{r}
= \int_{\mathcal{C}_2} \bm{A} \cdot \mathrm{d} \bm{r}
$$

となるからです。
そこで、始点と終点の位置ベクトルをそれぞれ $${ \bm{x}_0 , \bm{x} }$$ として上の線積分 $${ (\ast) }$$ を $${ U }$$ とおくと、$${ U }$$ は積分経路 $${ \mathcal{C} }$$ によらず、また始点は固定することにすると、$${ \bm{x} }$$ のみの関数として定まることが分かります。つまり

$$
U \left( \bm{x} \right) = \int_{\bm{x}_0}^{\bm{x}}
\bm{A} \left( \bm{r} \right) \cdot \mathrm{d} \bm{r} \qquad (\diamondsuit)
$$

と表すことができます。この線積分は積分経路によらないので、逆に言うと、計算しやすいように適当な経路を選んでよいことになります。成分表示 $${ \bm{x} = \left( x, y, z \right) }$$, $${ \bm{x}_0 = \left( x_0 , y_0 , z_0 \right) }$$ を使って経路を、例えば

$$
\left( x_0 , y_0 , z_0 \right) \longrightarrow \left( x , y_0 , z_0 \right)
\longrightarrow \left( x , y , z_0 \right) \longrightarrow
\left( x , y , z \right)
$$

ととることにします。この経路は

「$${ x }$$ 方向にのみ移動（$${ y, z }$$ 方向は固定）」
$${ \Rightarrow }$$「$${ y }$$ 方向にのみ移動（$${ z, x }$$ 方向は固定）」
$${ \Rightarrow }$$「$${ z }$$ 方向にのみ移動（$${ x, y }$$ 方向は固定）」

という経路で、固定されている方向についての積分を考えなくてよくなるので線積分を計算しやすい、というメリットがあります。この経路で $${ (\diamondsuit) }$$ は

$$
U \left( \bm{x} \right) = \int_{\bm{x}_0}^{\bm{x}}
\bm{A} \left( \bm{r} \right) \cdot \mathrm{d} \bm{r}
= \int_{(x_0 , y_0 , z_0)}^{(x,y,z)} \left( A_x \mathrm{d} x' + A_y \mathrm{d} y'
+ A_z \mathrm{d} z' \right) \\\ \\\
= \int_{(x_0 , y_0 , z_0)}^{(x,y_0,z_0)} A_x \left( x',y',z' \right) \mathrm{d} x'
+ \int_{(x , y_0 , z_0)}^{(x,y,z_0)} A_y \left( x',y',z' \right) \mathrm{d} y' \\\
\qquad + \int_{(x , y , z_0)}^{(x,y,z)} A_z \left( x',y',z' \right) \mathrm{d} z' \\\ \\\
= \int_{x_0}^{x} A_x \left( x',y_0,z_0 \right) \mathrm{d} x'
+ \int_{y_0}^{y} A_y \left( x,y',z_0 \right) \mathrm{d} y' + \int_{z_0}^{z} A_z \left( x,y,z' \right) \mathrm{d} z'
$$

となります。この $${ U }$$ に対して $${ \bm{A} = \nabla U }$$ であることが示せればよいわけです。上の $${ U }$$ を $${ x }$$ で偏微分すると

$$
\frac{\partial U}{\partial x} = A_x (x,y_0,z_0)
+ \int_{y_0}^{y} \frac{\partial A_y}{\partial x} \left( x,y',z_0 \right) \mathrm{d} y'
+ \int_{z_0}^{z} \frac{\partial A_z}{\partial x} \left( x,y,z' \right) \mathrm{d} z'
$$

となりますが、ここで $${ \nabla \times \bm{A} =0 }$$ から

$$
\frac{\partial A_y}{\partial x} = \frac{\partial A_x}{\partial y} \ , \quad
\frac{\partial A_z}{\partial x} = \frac{\partial A_x}{\partial z}
$$

であるので、これを使うと

$$
\frac{\partial U}{\partial x} = A_x (x,y_0,z_0)
+ \int_{y_0}^{y} \frac{\partial A_x}{\partial y} \left( x,y',z_0 \right) \mathrm{d} y'
+ \int_{z_0}^{z} \frac{\partial A_x}{\partial z} \left( x,y,z' \right) \mathrm{d} z' \\\ \\\
= A_x (x,y_0,z_0) + A_x (x,y,z_0) - A_x (x,y_0,z_0) + A_x (x,y,z) - A_x (x,y,z_0) \\\ \\\
= A_x (x,y,z)
$$

となることが分かります。同様にして

$$
\frac{\partial U}{\partial y} = A_y (x,y,z) \ , \quad
\frac{\partial U}{\partial z} = A_z (x,y,z)
$$

となることも示せるので、$${ (\diamondsuit) }$$ で定義した $${ U }$$ に対して $${ \bm{A} = \nabla U }$$ となることが示せました。

$${ (\diamondsuit) }$$ の式以下の説明は、上に代えて以下のように示すこともできます:

$${ (\diamondsuit) }$$ の式で、$${ \left( x, y, z \right) \longrightarrow \left( x + \Delta x, y, z \right) }$$ と $${ x }$$ 方向に $${ \Delta x }$$ 変化させることを考えると

$$
U \left( x + \Delta x, y, z \right) = \int_{(x_0 , y_0 , z_0)}^{(x,y,z)}
\bm{A} \left( \bm{r} \right) \cdot \mathrm{d} \bm{r}
+ \int_{(x,y,z)}^{(x+\Delta x,y,z)}
\bm{A} \left( \bm{r} \right) \cdot \mathrm{d} \bm{r} \\\ \\\
= U \left( x, y, z \right) + \int_{x}^{x + \Delta x} A_x \left( x' \right) \mathrm{d} x'
$$

となります。ここで $${ \Delta x }$$ を微小量として $${ \Delta x }$$ の一次までをとると

$$
U \left( x + \Delta x, y, z \right) \approx U \left( x, y, z \right) + \frac{\partial U}{\partial x} \left( x, y, z \right) \Delta x \ , \\\ \\\
\int_{x}^{x + \Delta x} A_x \left( x' \right) \mathrm{d} x' \approx A_x \left( x \right) \Delta x
$$

となるので、$${ A_x = \dfrac{\partial U}{\partial x} }$$ となることが分かります。これと同様にすると $${ A_y = \dfrac{\partial U}{\partial y} }$$, $${ A_z = \dfrac{\partial U}{\partial z} }$$ も示せるので、$${ \bm{A} = \nabla U }$$ となることが示されます。こちらの方が、先に述べた説明よりも簡単かもしれません。

このように、「1. あるいは 3. から 2. を示す」のは難しくなく、教科書・演習書にもよく載っていますが、「2. から 1. や 3. を示す」のはやや難しく、教科書を見ても省略されていることがあります。ベクトル解析の計算にある程度慣れた後で、この記事で扱っているような部分での論理的なつながりが気になる人もいるかもしれません。この記事がそのような人の理解の助けとなれば幸いです。

この記事が気に入ったらサポートをしてみませんか？