円の中にある小円の回転数の謎（解説）

問題はこちら：

答え：9回転

　大円の円周の長さは半径が10なので20πです。一方小円の方は半径が1なので円周は2π。よって大円は小円の10倍円周が長いことになります。とすると一見小円は10回転するように思ってしまいます。しかし実際は9回転と1回転少なくなります。

　「いやいや、滑らずに沿って回転しているんだから同じ距離分回転しないのはおかしいじゃないか！」そうなんです、この問題、感覚と微妙に一致しない所がポイントなんです。なぜ1回転少ないのか？

正方形で考えてみよう

大円ではなく1周が20πある正方形があるとします。これに内接する半径1の小円が滑らずに転がるとしましょう。円と違い正方形の一辺は直線なので、円はその接している直線の長さ分転がれます。例えば直線が6πなら、1周2πの小円は3回転します：

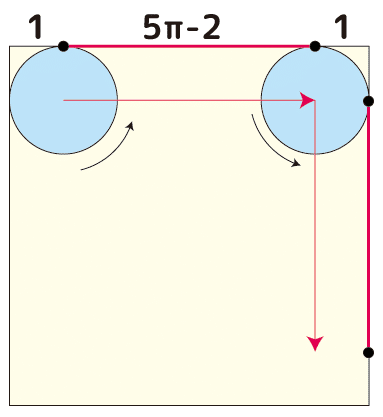
　上図の左上スタート位置から右方向にコロコロと右端まで回転した時、小円が接した部分は上の赤い直線となります。この長さは5π-2です。右に接した後は下方向に同じく5π-2だけ転がります。よって、正方形を1周すると小円は20π-8、およそ8.7回転する事になります。10回転には至りません。これは当然で、角の所に接しない部分があるのでその分距離が短くなるわけですね。

正N角形ではどうなる？

　では同様に1周100πの正N角形ではどうなるでしょうか？ポイントは小円が接する長さと接しない長さです：

上の図はN角形の角と半径1の円が接している様子を表しています。図の緑色の内角はπ/Nとなります。よってABの長さはtan(π/N)。1辺の長さは20π/Nなので、上図の赤い直線は20π/N-2tan(π/N)。よって1周回った時に円が接触する直線部分の合計（赤色部分の和）は20π-2Ntan(π/N)となります。

　正N角形はNの数が大きくなる程どんどん円に近付いていき、Nが無限大になると完全な円になります。よって上式のNの極限を取ると接触長が割り出せそうです。何となく20πになりそうな感じもするわけですが…実際どうなるか計算してみましょう：

上式でt=π/Nと置きます。するとNが無限大の時tは0に近付くので：

1/cos(t)はt→0で1です。一方sin(t)/tはt→0で1に漸近する事が知られています：

sinx/xについて覚えておくべき２つのこと | 高校数学の美しい物語

よって右式の三角関数の所は全部1となり、-2πが残ります。とても不思議な事に、無限大にまで多角形を細かくしても小円が接しない部分が必ず2πだけ存在するんです。

この計算結果から、小円は大円の円周から自身の円周である2π分少ない距離だけしか転がる事が出来ず、今大円は20πなので18π分、すなわち9回転するとなるわけです。

　この「2π分だけ転がれない」というのは、大円の半径が1、つまり小円と同じ場合を考えると少し納得しやすくなります。大円の内側に小円がピッタリくっ付いていると…スタートにいながらゴールもしている状態なので回転できないですよね。「回転できない長さ2π＝回転に関与しない長さ≒非接触な長さ」と考えると2πの意味が浮き上がります。

感覚と異なるこの問題、面白いですよね。ではまた(^-^)/