43枚の1、5、10円玉で100円を作る（解説）

問題はこちら：

答え：(1円, 5円, 10円)=(30枚, 12枚, 1枚), (35枚, 3枚, 5枚)

　答えは2通りあります。色々な解き方があると思いますが、ここでは小学生の皆さんでも出来る方法、そして不定方程式を用いたより理論的な方法の2通りの解答を紹介します。

解答1：鶴亀算で解く

　この問題は「鶴亀算」という考え方の発展で解く事ができます。鶴亀算は例えばこういう問題を解く事が出来ます：

『鶴と亀が合計で9匹います。足の合計が30本の時に鶴と亀はそれぞれ何匹いるでしょうか？』

　鶴の足は2本で亀の足は4本です。ここでもし9匹がすべて亀の場合、足の合計は36本になり6本オーバーしてしまいます。そこで亀1匹を鶴に置き換えると、足の本数は2本減って34本となります。1匹取り換える毎に足は2本減っていくので、36本を30本にするには足6本分、つまり6÷2=3匹だけ亀を鶴に置き換えれば良い事がわかります。つまり答えは亀が6匹、鶴が3羽とわかります。この一旦片方だけで足の数を合計し、溢れた（足りない）分をもう片方に置き換える事で補正して答えに近寄らせるのが鶴亀算です。

　同じような考え方を今回の問題に適用してみます。貨幣は全部で43枚です。もしこれが全部10円玉だった場合、430円となり大オーバーです。そこで10円玉1枚を1円玉に置き換えると差額9円だけ下がり421円になります：

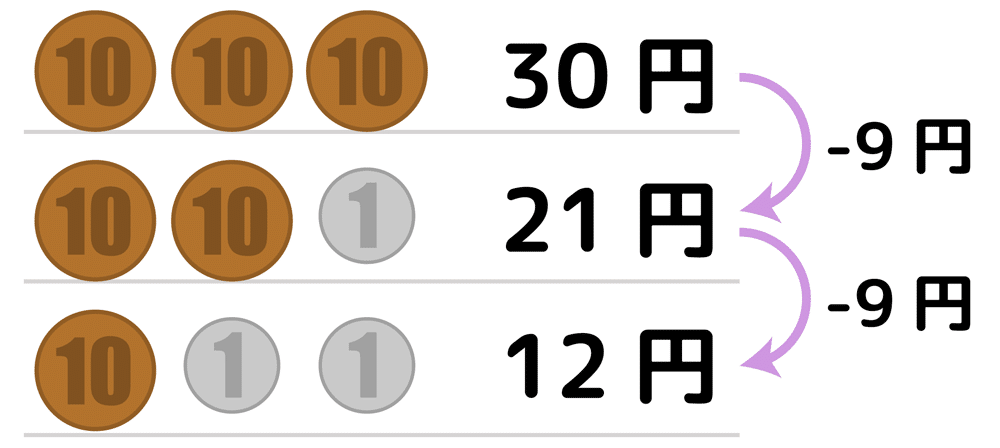
今430円で目標は100円なのでその差は330円。330円を差額9円で割ると36枚と余り6円。つまり1円玉36枚、10円玉43-36=7枚にすると合計が106円にまで近づきます。これを「(1円, 5円, 10円)=(36枚, 0枚, 7枚)=106円」と表す事にします。

　1円と10円で答の近くまで寄らせたので、残った5円玉を導入します。10円玉を5円玉に置き換えると5円下がります。一方1円玉を5円玉に置き換えると4円が上がります。ですから両方いっぺんに5円玉に置き換えると合計金額は5円-4円=1円下がる事になります。今106円と6円だけオーバーしていますから、両方を6枚、合計12枚5円玉に置き換えると丁度100円になる事が分かります。(1円, 5円, 10円)=(36-6=30枚, 12枚, 7-6=1枚)=100円が導けます。

　もう一つ別の道があります。(1円, 5円, 10円)=(36枚, 0枚, 7枚)=106円の段階で1円玉を5円玉で1枚だけ置き換えると4円上がって110円と切りの良い値段になります。(1円, 5円, 10円)=(35枚, 1枚, 7枚)=110円です。10円玉を5円玉に置き換えると5円下がるので、10円玉2枚を5円に置き換えると10円値下がりしてこれも丁度100円となります。つまり(1円, 5円, 10円)=(35枚, 2枚, 7-2=5枚)=100円も答えです。

　「110円に出来るのなら、さらに1円玉を5枚5円玉と差し替えれば+20円で130円になるはず。ここから10円玉6枚を5円玉に差し替えれば丁度30円分下がって100円になるのでは…」という発想は素晴らしいです。(1円, 5円, 10円)=(35枚, 1枚, 7枚)=110円から1円玉5枚を5円玉に差し替えます。(1円, 5円, 10円)=(30枚, 6枚, 7枚)=130円。ここから10円玉6枚を5円玉に差し替えると...(1円, 5円, 10円)=(30枚, 12枚, 1枚)=100円。これは最初の答えと一緒になります。

　「じゃあさらに1円玉を5枚5円玉に差し替えて+20円、150円にしたら？」やってみましょう。(1円, 5円, 10円)=(35枚, 1枚, 7枚)=110円から1円玉10枚を5円玉に差し替えて150円を作ります。(1円, 5円, 10円)=(25枚, 11枚, 7枚)=150円。10円玉を5円玉に差し替えて100円にするには10枚分差し替えが必要です。しかし10円玉は今7枚しかありません。つまり差し替え出来ないんですね。よって150円以上の値段は調べる必要がありません。

　以上から答えは2通りだけとなります。鶴亀算の応用でうまく43枚でえ100円を作れましたよね(^-^)

解答2：不定方程式を使って解く

　高校数学で習う不定方程式を用いると鶴亀算よりもより明確に答えを導けます。

　まず問題から次の2本の式が作れます：

a,b,cはそれぞれ1円玉、5円玉、10円玉の枚数で、上の式は合計金額、下の式は合計枚数との関係式になっています。上の式から下の式を引き算すると、

bとcが実数だとこれは無限に答えがあるのですが、今bとcは貨幣の枚数で0以上の整数。よってこれは不定一次方程式でして、これを満たすbとcの組み合わせは限られてきます。

　上式を次のように変形します：

右辺側を整数になる所とそうで無い分数な所に分離します。左辺のbは整数ですから右辺の分数部分も整数にならなければ辻褄が合いません。よって1-cは4の倍数であるとわかります：

mは整数です。cは10円玉の枚数ですからこれも0枚以上の整数。ここからmの範囲が、

つまりmは0以下の整数である事が判明します。

　c=1-4mをbの式に戻してあげると、

5円玉の枚数bもmで表す事が出来ました。このbも0以上の整数なので、mの範囲をさらに絞る事が出来ます：

先程のmの範囲と組み合わせると、mは、

つまり-1と0の2つだけである事がこれで判明します。よって、

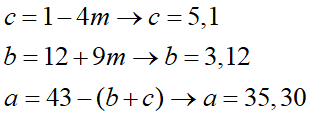
このように1円玉、5円玉、10円玉の各枚数がたちどころに導けました。2通りしか無いこともこれで納得ですよね。

深堀：合計金額と枚数を自由に設定できるようにする！

　今回の問題は合計金額が100円で枚数が43枚でしたが、これは他の合計金額や枚数にも勿論なれます。そこで合計金額をS円、枚数をT枚として、不定方程式で一般化してみましょう。

　まず方程式を2本立てます：

上から下を引いて、

ここから、

S-T-cが4の倍数である必要から、

またbは、

b,cはそれぞれ0以上である事からmの範囲は次のようになります：

このmの範囲式が欲しい式になります。この不等式に具体的な合計金額Sと合計枚数Tを入れれば、整数mの値が直ぐに導けて、そこから各貨幣の枚数がたちどころに求まってしまいます(^-^)

　例えば合計金額S=100円で合計枚数T=17枚と設定すると、上の式に代入して、

mが2つある事がすぐに求まり、ここから(a,b,c)=(0,14,3), (5,5,7)があっという間に求まります。

　S=100円、T=77枚とすると、

このようなmの範囲になり、整数となるmが範囲内に無い事が分かります。つまり合計77枚もあるのにどう頑張っても100円にはならないんですね（99円と101円にはなれます）。これ実は前後の76枚と78枚の時はちゃんと100円になるmがあるのですが、77枚だけぽっかりとmが無いんです(^-^)

　どうでしたでしょうか？鶴亀算でも行けますし、不定方程式を使うと不思議に答えが導かれて興味深いですよね。この理屈は貨幣の種類を変えても同じなので、色々な組み合わせで式を解いてみると面白いですよ。

ではまた(^-^)/