ABCDEF×DF=GABCDEF？（解答）

問題はこちら：

答え：140625×65=9140625

　問題の覆面算の答えは上のようになります。これ以外にはありません。これをどう導くか2つの方法で解説します。一つは愚直に考えて行く方法で、もう一つは少し時短できる方法です。

解説1：愚直に攻める！

　覆面算のコツは特徴のある個所に目星をつけてパターンを絞る事です。その線で愚直に攻めてみましょう。

　筆算を見てまず目につく特徴と言えば、各数字の1の位がすべて「F」になっている所ですよね。FにFを掛けて1の位がFになる掛け算は限られています：

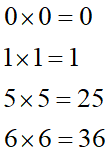
この4パターンです。

　まずF=0は、

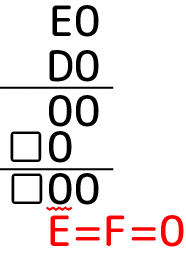
答えの下2桁目が0になりE=Fとなってしまう事からNG。

　F=1は

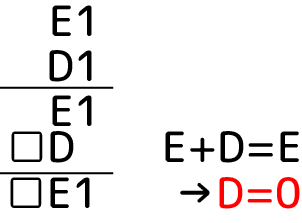
下2桁目の筆算が成り立つには右にあるようにD=0しかありません。しかしルールでDは0になれないためこれもNG。

　ではF=5はどうでしょうか：

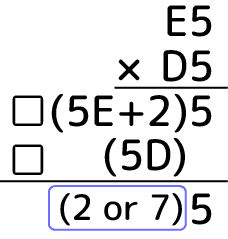
　以後(…)はまとめて1つの桁を表すとします。上の筆算から下2桁目は2か7とわかります。なぜならカッコ内の5Eと5Dはどちらも5の倍数なので、これら2つの合計の1の位は0か5しか取れません。それに繰り上がりの2を足すので2か7というわけです。

　E=2もE=7も可能性としてあり得るため、まずE=2を検討してみましょう：

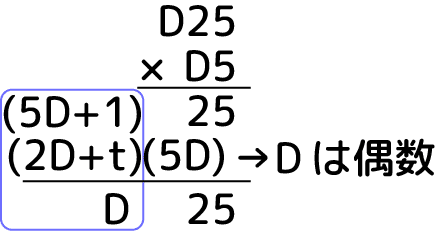
下2桁目の筆算は、

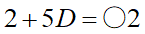
となります。1桁目が2になるDは偶数のみです。0と2は使えないため4か6か8のどれかとなります。ここで青い枠で囲った3桁目の筆算に注目します。上段の「+1」は繰り上がりです。tは下段の繰り上がりと2桁目の筆算で起こる繰り上がりを含めた値です。今Dは偶数ですから、上段の5Dは10の倍数。よって上段の下1桁は1で確定、つまり上段は奇数です。となると下段の答えも奇数にならないといけません。つまりtも奇数。青枠の左隣の2桁目の計算でtが5Dの10の桁である事は明白です（+2は繰り上がりに影響しない）。その繰り上がりが奇数になるDは…D=6のみですよね。つまり、

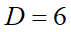
がここで確定します。

　続いて下4桁目の「C」の筆算…と行きたい所ですが、ここでもう一つ確定する物があります。それは「A」です：

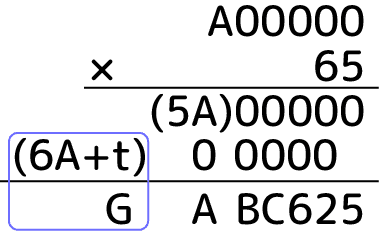
　仮に上のA以外の数字を0だとします。これに65を掛けると青い枠の7桁目のGが6A+tとなります。tは何らかの繰り上がりが来るわけですが、それを含めGは一桁なので6A+tは2桁になってはいけません。とすると、

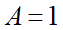
しか該当する数字がありません。これはBCDEFがあっても同様です。ここからGが6以上9以下である事もわかります。さらに言えば6はもう使われているため、Gは7,8,9のどれかです。大分情報が絞れて来ました。

　では改めて下4桁目の「C」の筆算に挑みましょう：

　下4桁目の筆算は青枠の足し算になります。ここで注目は上段の3と下段の7。これを足すと10です。5Cは5の倍数ですから、結果として青枠の下一桁は0か5にしかなれません。しかし5は既にFが使っているため、

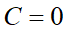
が確定する事になります。

　最後Bについて詰めて行きましょう：

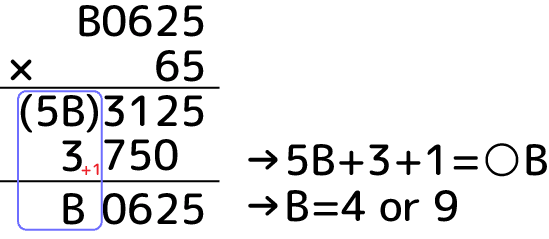
　青枠の筆算が成り立つBを考えます。下4桁目の筆算で1繰り上がるのに注意すると、

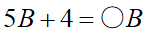
が成り立つBである必要があります。5Bは5の倍数ですから、左辺の結果右辺の1桁目がBの候補は4と9（24と49）。この段階でA～Fまで数字が揃っているので2通りを直接計算してみると、

B=4の時だけすべての条件を満たしているのが分かります。問題で答えは1通りと公言していますので、これが答えとなります。F=6の場合など他のパターンだと途中で矛盾が生じますので、お時間がある方は試してみて下さい。

解説2：ちょっとだけ時短な方法

　愚直な方法でも答えに辿り着きますが、式の性質を利用する事で少しだけ時短が出来ます。まず、

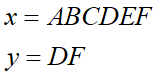
と置きます。最上位桁のGはそのまま使うとして、筆算の答えは、

と表せますね。そしてここから、

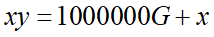
という等式が成り立つのもわかります。左辺をxでまとめて整理すると、

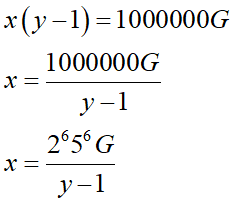
このような分数式を導けます。今xは自然数ですから右の分数も自然数にならなければなりません。つまりy-1は分子の約数になっているんです。

　ここでy-1の候補を考えても良いのですが、2桁とはいえ約数の数は結構あります。そこで愚直作戦に舞い戻ってみます。解答1でyは割と早い段階で65になるのが分かりました（F=5を仮定した場合ですが）。それを上式に代入すると、

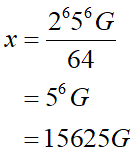
右辺から分数が消えました。今xは6桁ですからGは7～9のどれかである事がこの段階で分かります。後はそれらを放り込むと、

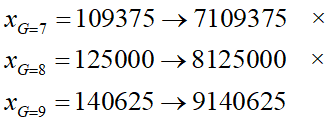
G=9の時にだけ条件を満たすのが分かります。

深掘：覆面算を作る

　今回の問題は「何かいい感じの覆面算出来ないかな～」とあれこれ思案している中で出来た1問です。程良い難易度だったので採用しました。深堀ではこういう感じの覆面算の問題をどうやって作るのかに焦点を当ててみます。

　覆面算にも色々なパターンがありますが、スタートは適当な桁数をアルファベットで表現する所から始まります。例えば、

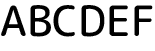
かな～みたいな。これに対して足し算するか掛け算するかなど演算方法を決めます。掛け算にすると決めたとして、掛ける数をどうするか次に考えます。桁数は1桁？2桁？数字は固定にするか覆面にするか…などです。とりあえず一桁の覆面にしましょう。もちろんこの段階でパズルとして成立するかは分かっていません：

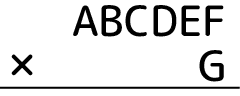
　答えの並びが覆面算のパズル性を決めます。これも色々考えられます。例えば全部同じ数字になるとか（PPPPPP）、掛けられる数の並びが逆になるとか（FEDCBA）。今回は最上位のAが最下位桁に来るとしてみましょう：

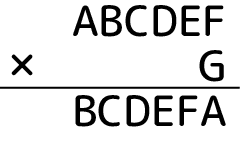
　後はこれが解けるか試してみるだけです。試し方はもちろん愚直にやっても良いですし、パソコンの力を借りるのもありです。上の場合は高々1000万通りですから、プログラムを組んで全通り試しても多分物の数秒でしょう。でも手計算で解くのも楽しいですから、今回は手を動かしてみます。

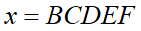
と置くと、筆算の式の関係から、

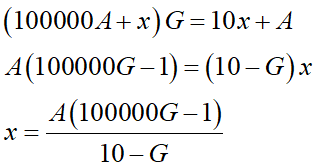
こういう方程式が導けます。左辺が筆算の上側の計算で、右辺が答えですね。整理すると下段の分数になります。

　Gは1桁で0では無いので、分母は1～9のいずれかです。一つずつ検証してみると、Gが偶数の時はどうにもうまく行かない事がすぐに分かります。括弧の中が奇数なので、分母を通分するにはAが10-Gの倍数にならないといけないんですが、括弧内が9999と続く数なので1や2などを掛けると桁の数字に重複が出ちゃうんですね。なのでGは奇数だろうと気付きます。

　G=1で分母が9の時はAが9かAが3で括弧内が3の倍数であれば良いのですが、いずれもうまく行きません。G=5,7,9の時も矛盾が出てしまいます。唯一G=3の時通分が成功して、

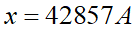
と右辺が自然数になります。5桁のxを満たすのはA=1,2の2通りあります。実際それを元の筆算に入れると、

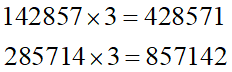
いずれも覆面算の条件を満たしています。

　ここから難易度調整をします。Gの値も伏せると検証するパータンが多くなって難易度が上がり手数も増えてしまいます。そこで「じゃぁGは3としようかな」「A=1は既知としようかな」などと考えます。最終的に、

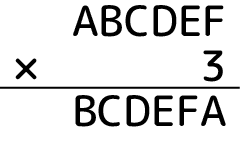
Gを3と公開して難易度を下げてパズルとして取っ付きやすくして完成です。ちなみにですが、上の問題は算数オリンピックで実際に出された問題です。

　こんな感じで筆算の構成を考えて、手計算やプログラムなどで解の存在を確認し、実際に解く手順を導けば覆面算の問題が1問出来上がりです。是非皆さんも覆面算の問題作成にチャレンジしてみて下さい。「これは難しいぞ！」という問題が出来ましたら是非教えて下さい！

ではまた(^-^)/