円をコンパスだけで4等分する作図（解説）

問題はこちら：

答え：√2を作図する！

この問題の鍵となるのは「√2」です。なぜなら半径に対して√2の円弧は、右図のように円周を丁度4等分してくれるからです。この√2を作図でどう出すかがポイントです。

解説：√2を出す

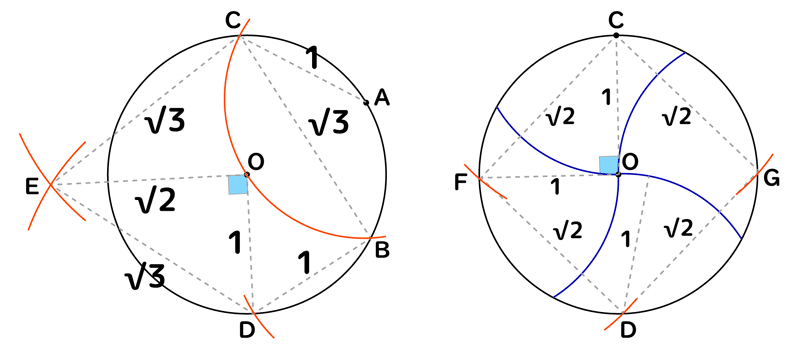
　円の半径を1としておきます。コンパスは円の半径と同じだけ開いています。この状態でまず円周上の適当な所（点A）から半径1の円弧を描き、それと円周との交点をB、Cとします。この時BC間の長さは√3になります。これで√3を取る事が可能になりました。

　コンパスはそのまま半径1だけ開いておき、次に点Bから点Dを取ります。こうすると線CDは円の直径となります（△OAC、△OAB、△OBDが合同な正三角形なので）。次にBCを使ってコンパスを√3に開き、点CとBから円弧を描き、点Eを取ります。△ECDは二等辺三角形で線CDが直径なので、点Eから降ろした垂線は円の中心Oを通り、∠DOEは直角になります。よって三平方の定理より線EOの長さは√2になります！これで√2も取れるようになりました（点Oは自明ですが点Dから半径1の円弧を描くとその交点で得られます）。

　ここからは右図に移ります。円周上の適当な所で良いのですが、分かり良いように点Cから√2の円弧を描き円周と交点FとGを取ります。この時△FCOは辺の比が1:1:√2の直角二等辺三角形になるので、∠COFが90度になるのがわかります。線CDは直径で孤CDは半円（∠CODが180度）であるため、点Fは孤CDの中点となります。同様にして点Gも孤CDの中点である事から、円周上の点CFDGは円周を4等分している事がわかります。後は右図の青い円弧のように点CFDG上から半径1の円弧を描くと、図形の対称性からその円弧で切り分けられた図形が合同で円を4等分している事になります。

余談：恩師の策略

　この問題は僕が中学の頃の数学の恩師が校内の3年生に出した問題で、1番に解けたらラーメンの商品付きという物でした。この出し方が今思い出して上手いなぁとにやけてしまうのですが、最初は6等分の問題から出題が始まりました。これは半径1の円だけで出来るためとても簡単で、大体の人が解けました。これで「あぁ、円周を等分して風車みたいに描けばいいんだ」という事を学べます。ここから2等分、3等分も簡単に導けます。みんなの中に「簡単じゃ～ん」な空気が出来ます。そこにきてこの4等分問題。「円周を4等分すればいいのね」はすぐにわかりますし、√2があれば良い事も気付けます。でも、その√2をどこで取れば良いかが思いつきにくいんです。解答を見れば一目瞭然ではありますが、ノーヒントで1:√2:√3の直角関係を見つけ、それをコンパスだけで作図するのは簡単ではありません。結局誰も解けずじまいでした。合同な図形を描く方法を6等分で導いて興味を沸かせてから本題に入る。授業として旨い策略だなぁと今思うと感心します。

チャレンジ：5等分は出来る？

　コンパスだけで4等分は出来ました。2、3、6等分は簡単です。では5等分はどうなのか…。これは僕も答えを知りません。もし出来た方は是非教えて下さい。

ではまた(^-^)/