円をコンパスだけで5等分する作図（解説）

問題はこちら：

答え：√5-1を作図する！

　半径が1の円に内接する正五角形の1辺の長さはちょっと面倒臭い値になります（後程示します）。それをコンパスだけで取るのは至難の業であるため、代わりに「半径が2の円に内接する正10角形の辺の長さ」を使います。この長さは√5-1でして（これも後述します）、左図の方法で計り取る事が可能です。正10角形を作れれば正5角形も簡単に作れるため、右図のように風車状に円弧を描けば内側の半径1の円も同時に5等分される事になります。

解説1：半径2の円に内接する正10角形の1辺の長さは√5-1

　この問題は正5角形の一辺の長さをコンパスで取ろうと考えると中々うまくいきません。それは半径1に内接する正5角形の一辺の長さが、

という2重根号になってしまうためです。これは直線を描けない条件では難し過ぎます…。そこで倍の正10角形に注目します。半径1の円に内接する正10角形の一辺の長さは、

になります（深堀で詳しく説明）。少なくとも2重根号でないのは有難い所です。ただ分子の値を「半分にする」というのもコンパスだけではシンドイのです（直線が引けるなら簡単）。そこで円の半径を倍の2にします。半径が倍になれば一辺の長さも2倍になります。よって、半径2の円に内接する正10角形の一辺の長さは、上に2を掛けて、

になります。「1」は元の円の半径そのものですからコンパスで取れます。なので後は√5さえ取れれば何とかなりそうです。

正10角形の一辺をコンパスで取れれば、1個飛びにすれば正5角形になりますから、後は簡単に5分割できます。という事で、この問題は半径1の円から√5-1、もっと言えば√5をコンパスで作れるかどうか？という問題に置き換える事が出来るわけです。

解説2：√7から√6を、√6から√5を

　半径1から√5を作ると聞いて真っ先に思いつくのはこれです：

半径1も直径2もコンパスで取れるので√5も簡単に作れそうなのですが、これが難しい…。直線が引けないので「1と2が直角になる所」をそもそもに作りにくいんです。

この問題で長さを作りやすい図式は以下かなと思います：

円周上で直径となる2点から長さ√aを取って交点Pを作ると、三平方の定理からOPの距離は√(a-1)になります。つまり、例えば斜辺に√3を与えるとOPは√2に、√4なら√3に...と中身が1だけ減った長さを作れるんです。ですからOP=√5にするには斜辺に√6を与えれば良いですね。でも√6…これもぱっと作れる感じはしません。ところが、ひとつ上の√7は実は簡単に取れます！以下をご覧く下さい：

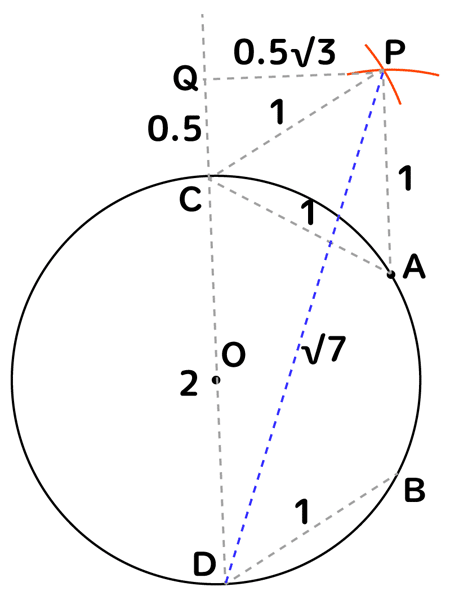
直径CDの点Cから半径1の距離を取って点Aとします。さらに点Cと点Aから距離1の交点Pを取ると、DPの距離が√7になります。理由は直角三角形DQPで三平方の定理から、

となるためです。

√7が取れれば先の長さを作る方法で√6が作れる、そして√6があれば同様にして√5が作れるわけです！

で、今本当に欲しいのは√5-1なんですが、これが大変うまい事に下の図のFHがずばりその距離になっています：

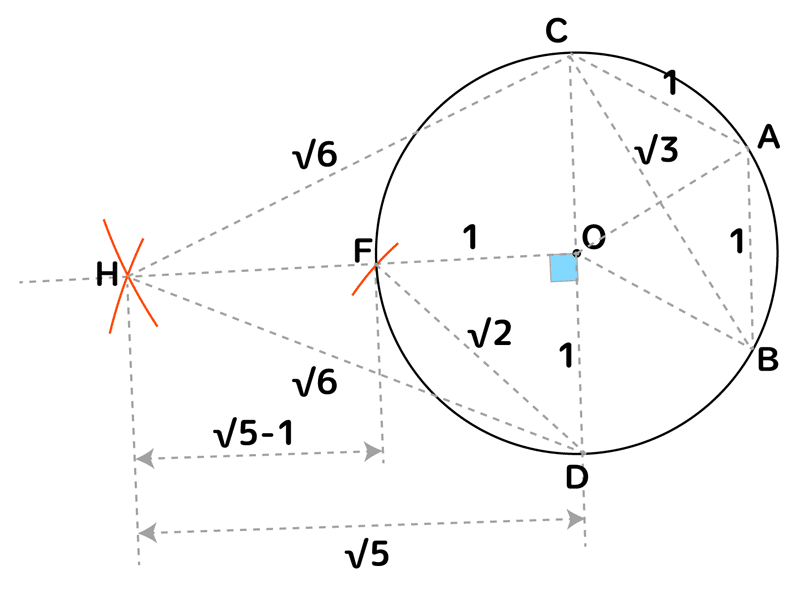
点Fは点Dから√2の長さで交点を作れば取れます。√2は先の距離を作る方法で斜辺に√3を与えれば取れます。√3は上のBCにありますね。OHの長さが√5で、円の半径が1なので、FHの長さは√5-1になります。

　という事でFHからいつでも√5-1を取れるようになるので、冒頭の右図のように中心点Oから半径2の円を描き、円周上の点Pから√5-1の距離の交点I、Jを取ると、そのIJが半径2の円に内接する正5角形の一辺の長さになっています。後はコンパスで円周を5等分して、その等分点IJKLMから半径2の円を風車のように描けば完了です。

深堀：正10角形の辺の長さ

　この問題を解くカギになったのが正10角形の一辺の長さです。この長さを実際求めてみましょう。三角関数を使わないので中学生でも理解できるはずです。

　まず、下のような正5角形の中に△ABCを作ります：

　∠Aは36°、∠Bと∠Cは72°なので△ABCは二等辺三角形です。ここでABの長さを1、BCの長さをaとしておきます。赤いのは比率と考えて下さい。BからACに向けて∠CBDが36°になるような点Dを取ると、△BCDも二等辺三角形になります。よってBDもaです。さらに△ABCと△BCDは相似なので、CDはa^2になります。次に△DABに注目すると、これも二等辺三角形になっていますから、BD=AD。よってADもaになります。

　ここでACがa+a^2になっているのがわかりますね。そしてAC=ABですからその長さは1です。つまり、

という関係式が成り立ちます。解の公式でaを求めると：

という事で、AB=1の時底辺BCは上の値になる事がわかりました。そこで次に△APQに注目します：

△APQも∠Aが36°の二等辺三角形なので、AQ:QP=1:aです。今APは直径なので半径を1とすると長さは2。という事はQPの長さは2aである事がわかります。正10角形の一辺は上図のBPになりますから、BPの長さは2a/2=a。つまりaそのものとなり、

となる訳です。

　半径が2の円の場合、これが2倍となるので、本問題を解くコアとなった√5-1が導けます。

　中々難解でしたがコンパスだけで円周を5等分出来るのはちょっと自分でも驚きました。解法を見つけた時は嬉しかったです。こうなると正7角形は…と欲が出てしまうのですが、流石に難しいかもしれません。もし方法がありましたら是非教えて下さい。

ではまた(^-^)/