欠けちゃった魔方陣（解説）

問題はこちら：

答え：以下の通り

　問題の欠けちゃったマスは上図のような数字の並びにすると魔法陣になります。行列斜めいずれも足して12になっていますよね。あれこれ試していればいずれ答えにたどり着くかとは思いますが、少し理詰めで考えてみましょう。

解説1：3x3の魔方陣を知っていれば一瞬

　もし3x3の魔方陣を知っていれば今回の問題は一瞬で終わります。3x3の魔方陣は実は以下の1種類しかありません：

ただし5以外の外側の数字を90度単位で回転してできる物、また上下左右を反転させた物は同一とします。

　今回の欠けちゃった魔法陣は1～8までの数字を一つずつ使う約束でした。でもです、これをあえて0～8までの9つの数字を使って普通の3x3の魔方陣を作ると考えたらどうでしょうか？

欠けた所を0と考えるわけです。これを作るのはとても簡単。先の3x3の魔方陣に並ぶ数字から1引けばいいんです。3x3の魔方陣はすべてのマスに等しい値を足し引きしてもやっぱり魔方陣になるんです！後は0の所を削っちゃえば完成です！

解説2：欠けた魔方陣のまま考える

　3x3の魔方陣を知らない場合に、問題のマスから並びを導く方法を考えてみましょう。

　そもそもですが、この欠けた魔方陣の行列斜めそれぞれの合計はいくつにならないといけないでしょうか？

　1列の合計をmとします。すると1行目、2行目、3行目はそれぞれ合計がmになりますよね。つまり1～3行目の全合計は3mです。一方1～3行目の合計は使用した1～8の数字の合計、つまり36です。と言うことは、

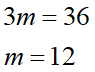
行列斜めの合計は必ず12でなければならない事がわかります。

　さて上のマスをご覧ください。3列目{d,e}と2行目{c,h}は2つの数字しか使いません。一方で1～8の数字で足して12になる組み合わせは、{8,4}, {7,5}の2種類しかありません。つまり3列目と2行目はこれらの数字で確定です。

　この欠けちゃった魔法陣は真ん中に水平線を引くと上下に対称です。その為3列目{c,h}に入る2つの数はどちらに入っても構いません。例えば上が8下が4でも、上が4下が8でも同じ事です。ここで注目はそのどちらにせよ「角にかならず8もしくは7が入る」という事実です。

　ここで真ん中の数字を考えます。合計が12で、右上角に8か7があるので、真ん中の数字は少なくとも4以下でなければなりません。5以上だとfが0以下になってしまいますよね。と言う事は2行目{d,e}は実は{8,4}しか合う物が無いんです。ここから3列目の角は7しか無い事も判明です：

　ここまでわかれば後は簡単。3マス中2マスの数字が埋まっている個所がありますので（aとf）、数字をどんどん埋めていけば以下のように各マスが確定します：

行列斜めの合計がそれぞれ12になっている事を確認すれば完了です。

深堀：角欠け、真ん中欠けの魔方陣も作れるか？

　ここからは深堀りです。今回の問題は辺のマスが欠けた物でした。では角や真ん中が1つ欠けた場合に1～8の数字での魔方陣が作れるのでしょうか？

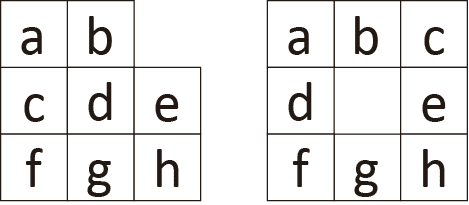
　結論から言うとこれは作れません。

　角や真ん中が1つ欠けた場合でも、1～8の数字を使うのなら行列斜めの和は12で変わりません。そして2つの数字を足して12になる組み合わせが{8,4},{7,5}の2つしかないのも一緒です。

　ところが角や真ん中が欠けると、数字が2つしかない列が3つ以上存在してしまいます。上左図の角欠けの場合、{a,b},{d,f},{e,h}の3つありますよね。右図の真ん中欠けは4つもあります。でも今使えるのは{8,4}と{7,5}の2セットしか無いんです。よって1～8の数字セットでこれらの魔方陣は作れないんです。

　ではちょっと条件を緩めて、1～8ではなくて重複しない整数なら何使っても良いよ～となった時にはどうでしょうか？これは出来ます！

　3x3の魔方陣を利用するなら、角の数字の一つが0になるようにすべてのマスに同じ値をマイナスすれば良いんです。例えば、

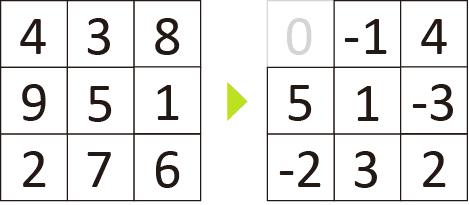
左の3x3の魔方陣の全マスを-4すると右のように角欠け魔法陣が作れます。ただし残念ながら連番には出来ません。

　3x3の魔方陣を使わず、ゴリゴリに計算してもOKです。試しに角が欠けた魔方陣を計算で作ってみましょう。

　上のように有効なマスにa～hまで記号を振ります。この行列斜めが同じ値mになるとすると、これは結局次のような「連立方程式を解く」問題に帰着します：

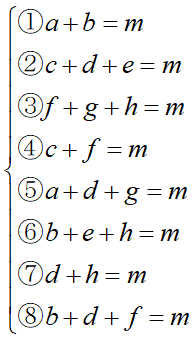
変数が9あるのに対して式が8本なのでこれは「不定方程式」です。ただし正数と限定しているので、答えが無限にあるのか、1通りなのか、それとも無いのかなどは実際に解いてみないと分かりません。

　式が8本もあって大変ではありますが、やる事は通常の方程式と一緒で、式にある変数を1つずつ消していきます。折角なのでちょっと丁寧にやりましょうか。

　まず①式を使ってbを消します：

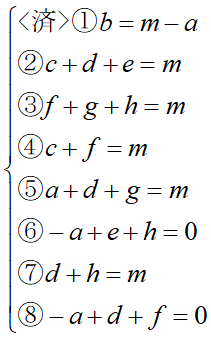
bがある⑥と⑧の式が変わりました。次は④を使ってcを消します：

②式からcが消えました。次は⑦を使ってdを消します：

②、⑤、⑧式からdが消えました。少しずつ変数が減ってきています。次ですが、⑤式を使ってhを消しましょうか：

⑥に特徴的な関係が現れました。eとgは絶対値が同じで互いに符号反転するようです。つまりeやgがゼロでなければ「角欠け魔法陣は必ず負数が存在する」事がここからわかります。その⑥式を使ってgを消しましょう：

②式からgが消えました。ここで面白い事が起きます。③式を整理すると②式と全く一緒になってしまいました。つまり残った有効な式は②と⑧の2本だけ。次が最後の変数消去となります。最後は②（③）式を使ってfを消去ですかね：

これで式を全部使いました。整理した⑧式を見ると、aとgが決まると行列斜めの和であるmが定まるようです。ただし3/2と分数が掛け算されているため、mが整数になるにはa+gは偶数である必要があります。要は{a,g}={偶数,偶数},{奇数,奇数}という事です。

　試しに{a,g}={2,4}とすると、m=9となり、後は芋づる式に他の変数が求まり、以下のようにマスが埋まります：

もちろんaとgを別の値にすれば別の数字セットになります。中には同じ整数が出現して条件を満たさない物もありますが、恐らく無限の組み合わせができます。

　全く同様にして真ん中が欠けたマスでも方程式を解く事が出来て、例えば以下のような数字セットで魔方陣になってくれます：

　真ん中欠けの場合、実は行列斜めの合計は必ずゼロにならないといけません。これは連立方程式を解いていく過程でm=0が出てくる事から分かります。面白いもんですよね～。

　と言う事で今回は欠けた魔方陣のお話でした。「欠けが1つじゃなく2つの場合でも魔方陣は作れるのか？」という疑問も湧いてきますよね。その場合3x3の魔方陣から足し引きではもう作れませんので、方程式をゴリゴリ解く事になります。できるのか出来ないのか、ぜひ試してみて下さい！

ではまた(^-^)/