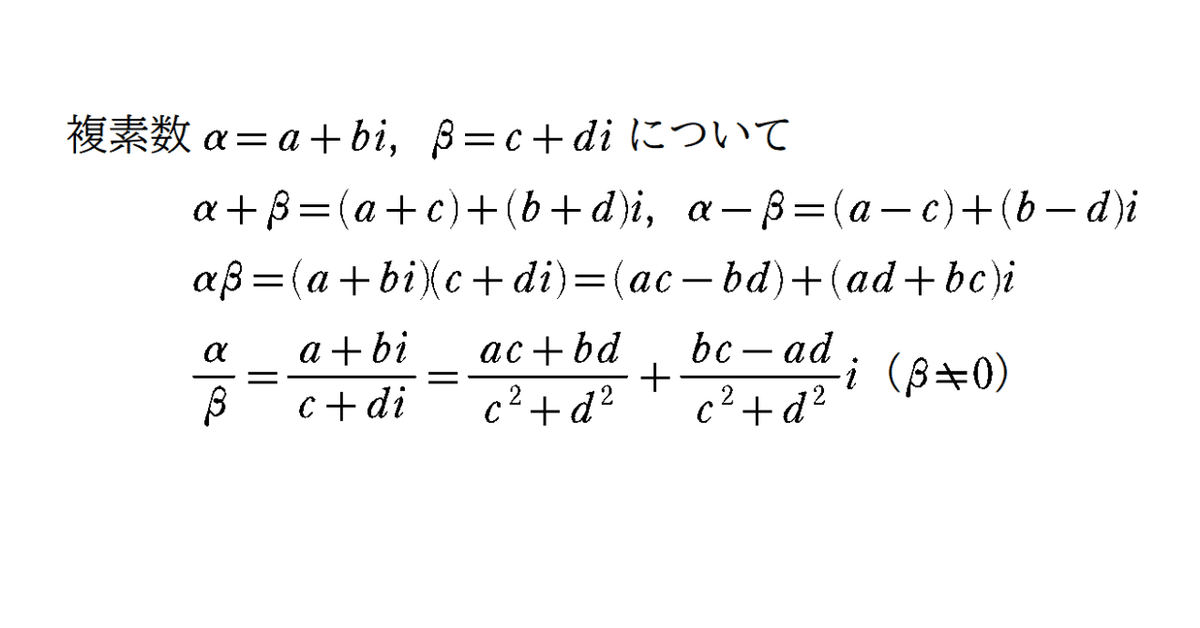
社会人のための学び直し数学【高校数学方程式編その３】

３．2次方程式②

　２で説明した $${\sqrt{\alpha}}$$  $${(\alpha>0)}$$ のような数については，次の計算規則があります。

$$
α>0,   β>0 として \sqrt{α}×\sqrt{β}=\sqrt{αβ}
$$

このことは，$${A^2=α,   B^2=β}$$ とすると，$${A=\sqrt{α},   B=\sqrt{β}}$$ なので $${AB=\sqrt{α}×\sqrt{β}}$$ であり，$${(AB)^2=A^2B^2=αβ}$$ より $${AB=\sqrt{αβ}}$$ であることから導かれます。

【注】指数法則から $${(AB)^2=A^2B^2}$$ であることを使いました。

例えば，$${\sqrt{2}×\sqrt{3}}$$ は $${\sqrt{2}×\sqrt{3}=\sqrt{2×3}=\sqrt{6}}$$ と計算します。
当然，$${(\sqrt{2})^2=\sqrt{2}×\sqrt{2}=\sqrt{2^2}=\sqrt{4}=2}$$ です。

　それでは，2次方程式 $${x^2=-q}$$ において $${q>0}$$ となる場合について考えていきましょう。
$${q>0}$$ となるとき $${-q<0}$$ となるので，$${x}$$ は平方（2乗）して負となる数となり，$${x}$$ が実数である限り，この方程式には解が無いことになります。（実数は平方すると必ず $${0}$$ 以上の数になることを思い出してください。）
そこで，2次方程式に解が存在するように，平方して負となる数を導入します。
　手始めに，$${i^2=-1}$$ となる数を考えます。$${\sqrt{-1}=i}$$ と書くこともあります。この $${i}$$ を虚数単位といいます。
虚数単位を使うと，例えば2次方程式 $${x^2=-5}$$ の解は $${x=\pm\sqrt{5}i}$$ となります。これは，
　　$${(+\sqrt{5}i)^2=(+\sqrt{5})^2×i^2=5×(-1)=-5}$$
　　$${(-\sqrt{5}i)^2=(-\sqrt{5})^2×i^2=5×(-1)=-5}$$
と計算できることを表しています。
$${\sqrt{α}}$$ という表現に $${α<0}$$ となる場合を許せば，解を
$${x=\pm\sqrt{-5}}$$ と書くこともできます。
ただ，この表現については注意が必要です。
先に述べた $${\sqrt{α}×\sqrt{β}=\sqrt{αβ}}$$ という規則を，そのまま適用すると
　　$${\sqrt{-2}×\sqrt{-3}=\sqrt{(-2)×(-3)}=\sqrt{6}}$$
となりますが，これは誤りです。
正しくは $${\sqrt{-2}=\sqrt{2}i,   \sqrt{-3}=\sqrt{3}i}$$ として
　　$${\sqrt{-2}×\sqrt{-3}=\sqrt{2}i×\sqrt{3}i=\sqrt{2×3}i^2=-\sqrt{6}}$$
としなければなりません。
このように，根号のなかに「$${-}$$」がある場合は，必ず虚数単位を使った表現にしてから計算することが大切です。

　2次方程式 $${x^2=-q}$$ に戻ると，$${q>0}$$ のときの解は

$$
x=\pm\sqrt{q}i
$$

となります。または，$${x=\pm\sqrt{-q}}$$ と書くこともできます。

　方程式の話題からはずれますが，虚数単位 $${i}$$ を使った数の計算の規則について少し触れておきましょう。

　$${a,   b}$$ を実数として，$${a+bi}$$ の形で表される数を複素数といいます。複素数で $${b\neq{0}}$$ となる数を虚数，特に $${a=0}$$ で $${b\neq{0}}$$ となるものを純虚数といいます。（もちろん，$${b=0}$$ となるとき $${bi=0×i=0}$$ と考え，複素数 $${a+bi}$$ は実数 $${a}$$ となります。また，$${a=0,   b=0}$$ のとき $${a+bi=0}$$ です。）

　2つの複素数 $${a+bi}$$ と $${c+di}$$ について，
　　$${a+bi=c+di}$$ ならば $${a=c}$$ かつ $${b=d}$$
が成り立ちます。
逆に
　　$${a=c}$$ かつ $${b=d}$$ ならば $${a+bi=c+di}$$
が成り立ちます。（複素数の相等）

　複素数の加法・減法・乗法・除法は，虚数単位 $${i}$$ を文字のように考えて計算して，$${i^2}$$ が出てきたところで $${i^2=-1}$$ と代入します。このことから，以下のように計算できます。

複素数 $${α=a+bi,   β=c+di}$$（$${β\neq{0}}$$）について

$$
\begin{gather*}
α+β=(a+c)+(b+d)i\\
α-β=(a-c)+(b-d)i\\
αβ=(a+bi)(c+di)=(ac-bd)+(ad+bc)i\\
\cfrac{α}{β}=\cfrac{a+bi}{c+di}=\cfrac{ac+bd}{c^2+d^2}+\cfrac{bc-ad}{c^2+d^2}i
\end{gather*}
$$

 $${αβ}$$ の計算を少し丹念に書いてみると，

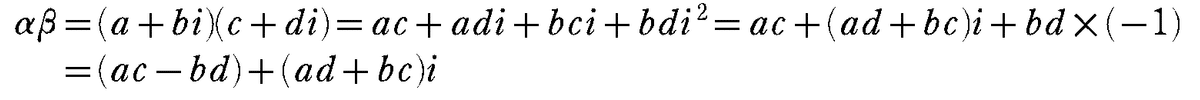
$${\cfrac{α}{β}}$$ の計算には，展開の公式 $${(x+y)(x-y)=x^2-y^2}$$ を使えるように，分母と分子に $${c-di}$$ をかけて

となります。

練習問題（1）2次方程式 $${x^2=-3}$$ を解け。

（2）$${1+\cfrac{1}{2}i+\cfrac{1}{1-i}}$$ を計算せよ。

【答】（1）$${x=\pm\sqrt{3}i}$$（2）$${\cfrac{3}{2}+i}$$
【解説】（2）分母に虚数を含むときは，
展開公式 $${(x+y)(x-y)=x^2-y^2}$$ 等を利用して，分母を実数に直します。

$$
\begin{align*}
1+\cfrac{1}{2}i+\cfrac{1}{1-i}&=1+\cfrac{1}{2}i+\cfrac{1+i}{(1-i)(1+i)}\\
&=1+\cfrac{1}{2}i+\cfrac{1+i}{1+1}\\
&=1+\cfrac{1}{2}i+\cfrac{1}{2}+\cfrac{1}{2}i\\
&=1+\cfrac{1}{2}+\left(\cfrac{1}{2}+\cfrac{1}{2}\right)i\\
&=\cfrac{3}{2}+i
\end{align*}
$$