多様体をバラバラに千切るために
本稿は 統治行為論 Advent Calendar 2022 21日目の記事です。詳細はカレンダーの概要欄をご確認ください。
名著『可換環論』の著者 として有名な統治行為論さんですが、2017年に放映されたアニメ「とぽろじっ!」に熱心だったように、低次元トポロジーにも造詣があるそうです!
胃の中はトポロジー的には身体の外部だが
— 統治行為論 (@t0uch1co) April 10, 2020
初耳だわ
そこで本稿では、低次元トポロジーにおいて基本的なツールとなっている、ハンドル分解について紹介します。
まとめ
ハンドル分解は多様体をキレイなパーツに分解するもので、その多様体の形状や性質をイラストに帰着させることができました。また比較的穏やかなハンドル分解をもつ多様体は分類が可能であることも分かりました!
………ということで、以降では上で述べたことについて水で薄めて引き伸ばしたような文章で解説していこうと思います。多様体に馴染みのない方や雰囲気だけ知りたい方は、文章を吹っ飛ばしてイラストだけパラパラ見てもらうくらいが丁度良いかもしれません。
またハンドル分解について「もっと詳しく知りたい」「教えてほしい」という勉強熱心な方は、統治行為論さん(@t0uch1co)のツイッターアカウントをフォローすることで発展的な内容について学べるかもしれません!
本稿は大まかに前後半の2部構成となっています。
前半ではハンドル分解について導入し、その具体例を確認していきます。そして後半ではハンドル分解を用いた応用例として、次のトピックについて紹介します。
1. 結び目の橋分解
2. 3次元多様体のHeegaard分解
3. 4次元多様体のトライセクション
1. 多様体のハンドル分解
ハンドル分解は「多様体の基本的なパーツ(ハンドル)への分割」です。多様体を図式(イラスト)で描画できるため、手で触れるように計算できます。
雑な言い換えとして、多様体を単体的複体と見たとき、構成要素の各単体を「太らせた」ものがハンドルとなります。
1-1. ハンドルとハンドル分解の定義
本稿でのおまじないとして、多様体を考える際には「向き付け可能である」ことを仮定します。また、$${n}$$次元球面と$${n}$$次元球体をそれぞれ $${S^n}$$と$${D^n}$$で記すことにします($${n \geq 0}$$)。
向き付け可能性に関する具体例として次のようなものがあります。
・向き付け可能な多様体:球面$${S^2}$$やトーラス$${T^2}$$
向き付け不可能な多様体:メビウスの帯、実射影平面$${\mathbb{RP}^2}$$
$${M}$$を境界成分を持つ$${n}$$次元多様体とします。ハンドルとは多様体$${M}$$へ「適切」に貼り付ける$${n}$$次元球体$${D^n}$$のことを言います。下にあるイラストは、3次元ボール$${M = D^3}$$にハンドルを接着している様子です。まるでマグカップの取手みたいですね!

正確な定義は次のようになります。大雑把に踏まえてほしい点は定義の後に箇条書きしたので、お気持ちだけ知りたい方はそちらを確認して下さい。
$${0 \leq k \leq n}$$を整数とする。このとき$${M}$$に接着する($${n}$$次元)$${k}$$-ハンドル$${h_k^n}$$とは$${n}$$次元球体$${D^k\times D^{n-k}}$$であって、境界成分$${\partial M}$$と$${\partial D^k \times D^{n-k}}$$を埋め込み写像$${\varphi: \partial D^k \times D^{n-k} \to \partial M}$$によって接着したものである。
$${k}$$をハンドルの指数、埋め込み写像$${\varphi: \partial D^k \times D^{n-k} \to \partial M}$$を接着写像、そして$${\partial D^k \times D^{n-k}}$$また$${\varphi(\partial D^k \times D^{n-k})}$$を接着領域という。
$${n}$$次元の多様体用のハンドルは$${n+1}$$種類あり、それぞれ$${k}$$-ハンドルと呼称される($${k = 0, 1, \ldots, n}$$は指数と呼ばれる)。
ハンドルの違いは$${M}$$に接着するときの接着面の違いにある。
その接着面(接着領域)は$${S^{k-1}\times D^{n-k}}$$という形である。
ハンドルはその接着するための接着領域の形が重要です!
また冒頭で述べた「単体的複体での言い換え」を用いると、指数$${k}$$のハンドルは$${k}$$次元単体を太らせたものに対応しています!
多様体のハンドル分解は、ハンドルを次々に接着していくことによってその多様体を構成していきます。また基本的な性質として、全ての多様体はハンドル分解を許容します。ハンドル分解のお気持ちを知りたい方は次節にある具体例を確認して下さい。
多様体$${M}$$の分解$${M = h_1 \cup h_2 \cup \cdots \cup h_r}$$がハンドル分解であるとは、次を満たすことを言う:
$${M_{i-1} = h_1 \cup h_2 \cup \cdots \cup h_{i-1}}$$とするとき、$${h_{i}}$$は$${M_{i-1}}$$に接着するハンドルである。但し$${M_0 = \emptyset}$$とする。
1-2. 1次元のハンドル
1次元ハンドルの指数$${k = 0, 1}$$は2種類あるので、それぞれについて確かめましょう。
0-ハンドルの接着領域は次のようになります:
$${\partial D^0 \times D^1 = \emptyset \times D^1 = \emptyset}$$
そのため多様体$${M}$$への0-ハンドルの接着は、非交和$${M \cup D^1}$$となります。1-ハンドルの接着領域は次のようになります:
$${\partial D^1 \times D^0 = \partial D^1 (\approx S^0)}$$(端点の2点)
下のイラストにおける赤色の箇所が接着領域です。

お気持ち表明としてハンドルは曲げて描いています
円周$${M = S^1}$$を例にハンドル分解を考えてみましょう。次のイラストには実際に円周をハンドル分解したものを描いています。上側のハンドル分解は、所謂、一番簡明なハンドル分解$${S^1 = h_1^0 \cup h_2^1}$$になります。また少し非自明な例として、イラストの下側では$${S^1}$$の8個のハンドルによるハンドル分解を取り上げています。
$${S^1 = h_1^0 \cup h_2^0 \cup h_3^0 \cup h_4^1 \cup h_5^1 \cup h_6^0 \cup h_7^1 \cup h_8^1}$$
ここで、各ハンドル$${h_i^k}$$の指数部分$${k}$$は、そのハンドルの指数を表しています。

円周の非自明なハンドル分解の例(イラスト下)
具体例から想像がつくように、円周$${S^1}$$の極小点に対して0-ハンドルを考え、極大点に対して1-ハンドルを考えることでハンドル分解を巧く構成することができます。
1-3. 2次元のハンドル
1次元のときと同様に、2次元ハンドルについても実例を踏まえながら確認していきましょう。2次元なので、ハンドルの指数(指数)は$${k = 0, 1, 2}$$の3種類となります。
0-ハンドルの接着領域は次のようになります:
$${\partial D^0 \times D^2 = \emptyset \times D^2 = \emptyset}$$
多様体$${M}$$への0-ハンドルの接着は、非交和$${M \cup D^1}$$となります。1-ハンドルの接着領域は次のようになります:
$${\partial D^1 \times D^1 = S^0 \times D^1 \approx D^1 \cup D^1}$$(2つの円板)
下のイラストにおける赤色の箇所が接着領域です。2-ハンドルの接着領域は次のようになります:
$${\partial D^2 \times D^0 = \partial D^2 (\approx S^1)}$$
下のイラストにおける赤色の箇所が接着領域です。

次のハンドル分解のイラストは、2次元多様体であるトーラス($${= S^1\times S^1}$$)を4つのハンドルに分解する様子です。
$${T^2 = h_1^0 \cup h_2^1 \cup h_3^1 \cup h_4^2}$$
なお、各ハンドル$${h_i^k}$$の指数部分$${k}$$は、そのハンドルの指数を表しています。

3次元のハンドルも紙面上で具体的に描くことができます!例えば、一番最初に紹介したマグカップなハンドルのイラストは3次元の1-ハンドルです。他の指数のハンドルが気になった方は実際に接着領域を計算してみるとよいかもしれません(詳細は[松本]を参照)。
1-5. ハンドル分解とホモロジー群
ハンドル分解によって多様体を分解することができましたが、その分解パーツを(コ)ホモロジーによってある程度理解することが可能です!
複体のコホモロジーが定義された うれしい(うれしいんですか?(うれしそう))
— 統治行為論 (@t0uch1co) October 12, 2020
これにはコホモロジー好きの統治行為論さんもニッコリ
(Morse不等式)$${M}$$を向き付け可能で閉じている$${n}$$次元多様体とし、$${b_i(M)}$$を多様体$${M}$$の$${i}$$次ベッチ数(つまり$${i}$$次ホモロジー群のランク)とする。
$${M = h_1 \cup \cdots \cup h_r}$$を$${M}$$のハンドル分解とし、$${m_i}$$を指数$${k}$$のハンドルの個数とする。
このとき、各$${i}$$について$${b_i(M) \leq m_i}$$が成り立つ。
単体的ホモロジー群を例にとれば、各次元のホモロジー群は「単体たち(サイクル)」によって生成元されていました。そのことを反芻すれば、自然な不等式であることが実感できるのではないでしょうか。
2次元ハンドルの節で紹介したトーラスのハンドル分解は、モース不等式の等号が成り立つ例となっています。また、ハンドルの個数の交代和はオイラー標数と一致します!
$${\chi(M)}$$を$${M}$$のオイラー標数とするとき、次が成り立つ:
$${\chi(M) = m_0 - m_1 + m_2 - \cdots + (-1)^n m_n.}$$
1-6. ハンドル分解とMorse理論
本稿では割愛してしまいましたが、ハンドル分解と密接に関わっている重要な理論としてMorse理論があります。簡単ではありますが紹介します。
多様体$${M}$$から実数直線$${\mathbb{R}}$$への(滑らかな)連続写像$${h: M \to \mathbb{R}}$$を考えます。Morse理論とは、この連続写像の臨界点(極大点や極小点など)たちが多様体のハンドル分解に対応している、という理論です。
滑らかな連続写像$${h: M \to \mathbb{R}}$$の全ての臨界点が非退化であるとき、$${h}$$をMorse関数という。Morse関数の各臨界点は指数と呼ばれる値が定まる。すると指数$${k}$$の臨界点の近傍は指数$${k}$$のハンドルに対応し、多様体$${M}$$のハンドル分解が与えられる。
2. ハンドル分解の使用例
ハンドル分解の紹介をしたので、実際の使用例をいくつか見てみましょう。
2-1. 結び目の橋分解(n = 1)
最初に、橋分解と呼ばれる結び目のハンドル分解を紹介します。
結び目とは3次元空間($${\mathbb{R}^3}$$または$${S^3}$$)内の(連結な)閉曲線を言います。素朴ですね。
素朴ってなに?
— 統治行為論 (@t0uch1co) April 23, 2020
3次元空間内のある平面によって結び目を分割している状況を考えます。この分割が「キレイな」ハンドル分解を与えるとき、その分解を結び目の橋分解といいます。
3次元空間内の高さ関数$${h: \mathbb{R}^3} \to \mathbb{R}}$$を考える。すると結び目は$${h}$$に関して極大点と極小点を持つ。3次元空間内の平面が、結び目の極大点全体と極小点全体を分離するとき、その平面は結び目の橋分解を与える。
次のイラストは実際に橋分解を与える平面(青色)と結び目のハンドル分解(橋分解)です。

青色の平面は結び目の極大点と極小点を分離するように結び目を分断している。
コレによってハンドル分解は結び目を簡単なパーツに分けることができ、例えば次のようなことが知られています。
2-2. Heegaard分解(n = 3)
次に閉じている3次元多様体$${M}$$のハンドル分解の応用例であるHeegaard分解を紹介します。一般に、3次元多様体は目には見えない多様体であるため、実物をイラストで描くことができず感覚的に理解することが難しいですが、ハンドル分解を経由することでイラストとして描くことが可能となります。このときに登場するのがHeegaard分解です!
Heegaardさんは「ヒーガードさん」や「ヘガードさん」と呼ばれていることが多いように思います。さまざまな呼称がある点は、統治行為論さんと近しいですね!
Heegaard分解は、先ほど紹介した結び目の橋分解と同様、3次元多様体を2つのパーツに分解するものです!
…と言っても3次元のハンドルは3+1=4種類あるのでハンドルそのままで「分解!」と終わらせる訳にはいきません。そこで登場するのがハンドル体と呼ばれる3次元多様体です。ハンドル体は下のイラストのような、(むき付け可能な)閉曲面の中身が詰まっているような多様体です。
1つの0-ハンドルに$${g}$$本の1-ハンドル($${g \geq 0}$$)を接着して得られる、(境界成分を持つ)3次元多様体を(種数$${g}$$の)ハンドル体という。特に種数$${g = 0}$$のハンドル体は球体、種数$${g = 1}$$のハンドル体はトーラス体とも呼ばれる。

実は、0-ハンドルと1-ハンドルだけで構成された3次元多様体は全てハンドル体(の和集合)になることが図形をグニグニすることで分かります!それだけでなく、次の事実も成り立ちます!
(3次元)2-ハンドルと3-ハンドルだけで構成された3次元多様体もハンドル体(の和集合)となる。
これによって3次元多様体を「0,1-ハンドルからなるハンドル体」と「2,3-ハンドルからなるハンドル体」の2つに分解することが可能となります。この分解をHeegaard分解と言います(詳細については、[森元]を参照して下さい)。
(向き付け可能で閉じた)3次元多様体$${M}$$が$${2}$$つのハンドル体$${H_1, H_2}$$に分解されているとき、その分解をHeegaard分解という。
$${M = H_1 \cup H_2}$$
これによって3次元多様体という目に見えない図形を目に見えるハンドル体という図形に分割することができました!そして2つのハンドル体の「張り合わせ方」をハンドルに描き込むことで3次元多様体を紙面上に描くことが可能となります!その図式をHeegaard図式と言います。図式の描き方についても紹介したいのですが、いろいろと書くことが多いため、本稿では割愛させていただきます。下の図式は3次元多様体$${M = S^2 \times S^1}$$のHeegaard図式です。

そして最後にHeegaard分解から分かる事実として、例えば次のようなことがあります。
閉じた3次元多様体のハンドル分解によるハンドルの総数は偶数である。
ハンドルの総数が2つのとき、$${S^3}$$と(微分)同相である。
ハンドルの総数が4つとなる3次元多様体たちは完全に分類されている(レンズ空間と呼ばれます)。
結び目の橋分解で紹介した完全な分類は、このレンズ空間の分類から得られる事実です!3次元多様体のHeegaard分解と結び目の橋分解は密接に関わっているということですね。
2-3. トライセクション(n = 2, 4)
1,3次元の多様体については橋分解とHeegaard分解という分割がありました。これに類似する偶数次元の多様体の分解として、近年導入されたトライセクションがあります。トライセクション (trisection) は名前にもある通り4次元多様体を3つのパーツに分割するものです。
我が家はシングルベッドを縦に3つ並べています 床はないです
— 統治行為論 (@t0uch1co) October 23, 2022
統治行為論さんの邸宅もトライセクションされているそうです。
Q. なぜ2つではない?:奇数次元の多様体が2つに分解できた大きな理由にハンドルの種類が偶数であったことが挙げられます。そのため、偶数次元で似た議論を行おうとすると、指数が丁度真ん中のハンドルが残ってしまうため、上手く分解することは難しいです。
トライセクションの定義を確認しましょう。4次元多様体$${M}$$が(1-)ハンドル体であるとは、(3次元の場合と同じで)ハンドル分解として0-ハンドルと1-ハンドルのみからなるものを持つものをいいます。同値な言い換えとしては、1つの0-ハンドルと複数個の1-ハンドルからなる4次元多様体です。そして多様体$${M}$$のトライセクションは、$${M}$$を3つのハンドル体へキレイに分割することをいいます。
向き付け可能な閉4次元多様体$${M}$$のトライセクションとは、次の3つの条件を満たすような多様体の分割$${M = X_1 \cup X_2 \cup X_3}$$である。
(1) 各$${X_i}$$は(1-)ハンドル体である($${i = 1,2,3}$$)。
(2) $${ \Sigma = X_1 \cap X_2 \cap X_3}$$は$${\partial X_i}$$内の閉曲面である($${i = 1,2,3}$$)。
(3) $${\partial X_i = (\partial X_i\cap \partial X_j) \cup (\partial X_i \cap \partial X_k)}$$はHeegaard分解である($${\{i,j,k\}= \{1,2,3\}}$$)。
簡単な具体例をいくつか紹介します!
まず一番簡単な例として4次元球面$${M = S^4}$$のトライセクションを考えましょう。すると3つの4次元球体$${D^4}$$への分解がトライセクションになります。これについては、2次元球面を用いて想像してもらうと理解が進むかもしれません。

上の2次元球面$${S^2}$$の場合でトライセクションの条件を見てみましょう。
(1) 各$${X_i}$$は$${D^2}$$と同相(4次元のとき$${D^4}$$)
(2) $${ \Sigma = X_1 \cap X_2 \cap X_3 \approx S^0}$$は2点集合(4次元のとき$${\Sigma \approx S^2}$$)
(3) $${\partial X_i \approx S^1}$$であり、$${S^0}$$によって2つの線分への分割されます(4次元のとき$${S^3}$$を2つの$${D^3}$$に分割)
別の具体例として$${M = S^3 \times S^1}$$のトライセクションを考えましょう。$${S^4}$$のトライセクションの議論を辿ることで、3次元球面$${S^3}$$も同様に3つの$${D^3}$$へ分割することができます。それぞれの球体を$${B_1, B_2, B_3}$$としましょう。そして$${X_i = B_i \times S^1}$$($${i =1, 2, 3}$$)と定めると、$${M = S^3 \times S^1}$$の分割を得ます。
$${S^3 = B_1 \cup B_2 \cup B_3, \quad B_i \approx D^3~(i = 1, 2, 3)}$$
$${S^3 \times S^1 = X_1 \cup X_2 \cup X_3, \quad X_i =B_i \times S^1~(i = 1, 2, 3)}$$
この分解は$${S^3\times S^1}$$のトライセクションとなります。実際にトライセクションの条件を満たしていることは、「$${X_i}$$の境界が$${S^2\times S^1}$$である」や「$${D_1 \cap D_2 \cap D_3 \approx S^1}$$である」ことを確かめることで確認できます。興味のある方は実際に計算してみてください。
ここで3次元多様体のHeegaard分解と結び目(1次元)の橋分解が密接に関係していたように、4次元多様体のトライセクションも、4次元多様体内の閉曲面の分解を与えることできます!この曲面の分解は橋トライセクション (bridge trisection) と呼ばれています。
……ただ、これ以上の内容の紹介は少し発展的であるため、詳細は割愛します。興味のある方は原論文を読んでみたり、また日本語での文献もいくつかネット上にあるので探してみてください。統治行為論さんをフォローするのも良いかもしれません。
2-4. その他
本稿では主にHeegaard分解とトライセクションに注目したハンドル分解の応用例について紹介しましたが、その他にもとても有用かつ楽しい表示が知られています。
例えば、4次元多様体のハンドル分解を用いることによってKirby図式と呼ばれる結び目を用いた4次元多様体の表示が構成できます。さらにKirby図式を用いて3次元多様体を表示することができます。
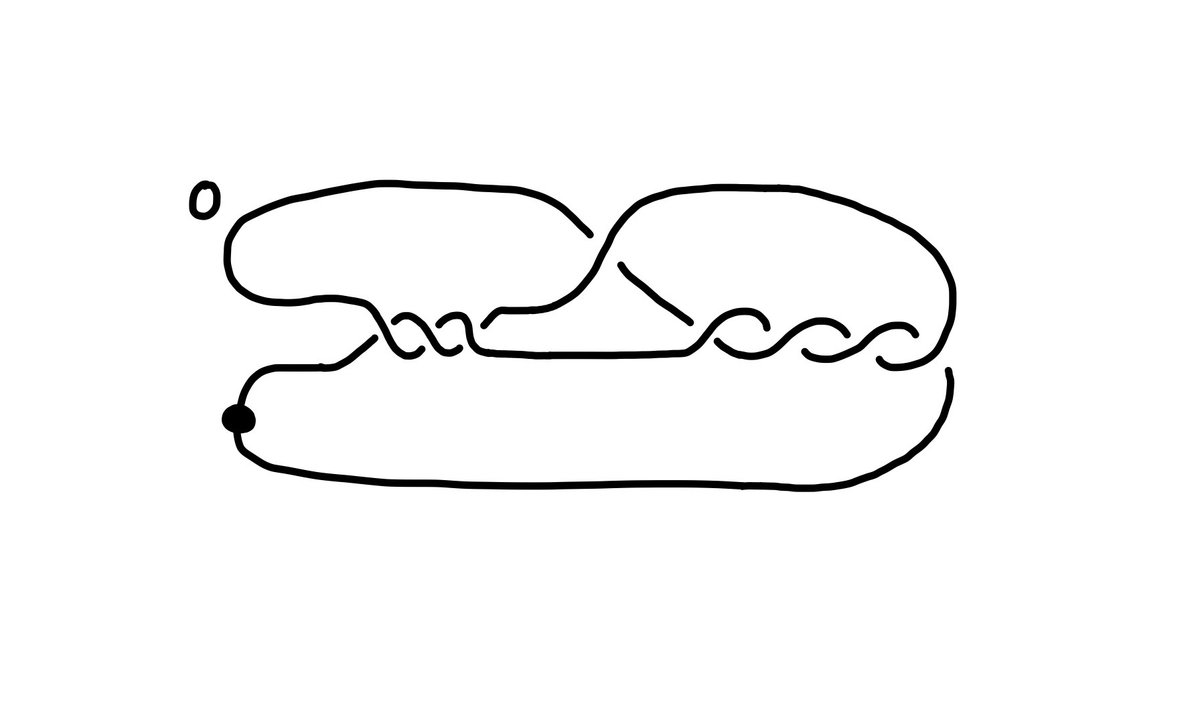
3. 文献など
統治行為論さんは積読に熱心なので、参考にした文献をいくつか列挙したいと思います。「参考にした文献」と「引用している文献」が異なっている点はご容赦ください。
松本幸夫 - Morse理論の基礎(岩波書店)
多様体の基礎のような分かりやすさでモース理論とハンドル分解について勉強できます。自主セミナーに丁度よさそう。J. Milnor - Lectures on the H-cobordism Theorem(Princeton Univ. Press)
モース理論をもう少し一般的な状況で勉強できるらしいです。1章だけ読んで積読してる。A. Hatcher - Algebraic Topology (Cambridge Univ. Press)
代トポの辞書的なヤツ。証明が読みやすい(個人的感想)のでいつか読了したい。つまり積んである。ご本人がカラー版を公開しているため、単語検索をする際にはとても便利です。R. Gompf and A. Stipsicz - 4-Manifolds and Kirby Calculus(AMS)
4次元多様体の教科書といえばコレみたいな本。いつか読了したい。内容だけでなく、キレイなイラストがたくさん掲載されいるため、図録見たいな感覚でパラパラと見るのも楽しいです。
4. 終わりに
いかがでしたか?
本稿を通して皆さんに低次元トポロジーの雰囲気を感じ取ってもらえていれば幸いです。
また今週末にはアニメ「ぼっちざろっく」の最終回を迎えますが、第一話から最終話まで目を離せません。個人的にはSick Hackの劇中歌「ワタシダケユウレイ」のフルがどんな曲なのかワクワクします。
さらに、年末には結束バンドのアルバムが発売されます!買いましょう!
アルバム 12/28 発売
— 統治行為論 (@t0uch1co) November 12, 2022
すげえ
明日のアドベントカレンダーは、おっくーさんが統治行為論さんに毎日詩を書いてうつ病にさせてみたそうです!
この記事が気に入ったらサポートをしてみませんか?
