
最強の定義、存在可能性とメタゲーム推移
1. 最強に迫る
最強の定義
”最強デッキ”
TCGプレイヤーにとって最も心躍る単語の一つである。最強デッキを見つける度に私も含む競技プレイヤーはデッキを考えては試している。
しかし最強の定義ははっきりしていない。
最強定義1「全デッキに対して50%以上の有利がつくデッキが最強デッキだ」
最強定義2「全てのデッキに対する平均勝率が最大のデッキが最強デッキだ」
どちらも違和感がないのではないだろうか。どちらの定義を示されても納得する人が大半だと思う。しかしこの二つの定義は異なる場合がある。
例えばここにただ3つだけのデッキが存在する世界Xを想定してみよう。デッキAはデッキBに99%勝つことができる。デッキAとデッキCはデッキBに51%で勝つことができるとする。

この世界で最強定義1に従えば、デッキCが最強デッキだ。デッキCに対して五分を超える相性のデッキは存在しない。
最強定義2に従えば、デッキAが最強デッキだ。デッキAの世界に存在しうるデッキへの平均勝率は74%であり圧倒的である。
どちらの最強定義が真実に近いだろうか?
例えばMTGAのランク戦では最強定義2の平均勝率がより近いのではないかと思う。ランク戦では順位がついてはいるが、順位を1位にしたところで何も起こらない。勝つことよりも好きなデッキ、使いたいデッキを使うというインセンティブが強い。そのため、勝つことを優先した合理性はあまり期待できない。
それに対して、CS予選、CSと大会の参加者のレベルが上がると勝つことに対し価値を感じるプレイヤーの割合が増える。プレイヤーのレベルも上がり、他のプレイヤーの合理性を信用できるようになる。
合理的な相手を想定して世界Xのメタゲームをもう一度見る。ここでデッキBを使った場合、デッキAを使った場合と比べ相手がどのデッキを使った場合に対しても勝率が低いことがわかる。デッキAではなくデッキBを合理的なプレイヤーが選択する可能性は排除できる。このような状態をゲーム理解の用語でAを選ぶ戦略はBを選ぶ戦略を支配しているという。デッキBが選ばれることがなければ、Bの排除されたAとCだけのメタゲームを考えればよい。そしてこのAとCだけの世界ではCを選ぶ戦略が支配戦略である。
合理的なプレイヤー同士であればお互いが最強定義1による最強デッキであるデッキCを選択した状態になる。そして使用デッキを変更することにより勝率を上げることはできない。このような「どのプレーヤーも戦略を変更によりより高い利得を得ることができない戦略の組み合わせ」をナッシュ均衡という。
最強定義2による最強デッキを全プレイヤーが選択している状態はナッシュ均衡である。
最強の存在可能性
ナッシュ均衡点では最強定義1によるデッキが選ばれる。では、逆にナッシュ均衡点を求めることが最強定義1による最強デッキを求めることかと言うとそれは違う。最強定義1による最強デッキが存在しないことがあるからだ。
デッキの相性が存在し、じゃんけんのように三つのデッキがお互いをけん制し合うような場合がある。
じゃんけんには決定的なある手を出すという純粋戦略はナッシュ均衡点にはない。グーとチョキとパーを確率的に出すという混合戦略が解である。
じゃんけんのような綺麗な対称性がないTCGでは純粋戦略の解が存在するのでは?と思う読者がいるかもしれない。しかし、対称性が歪んでいても混合戦略が解となることはある。例えばじゃんけんでチョキだけ例外的に25%でグーに勝つことがあるとしよう。勝ちを1、負けを-1の利得とすると、このゲームでのナッシュ均衡点でプレイヤーが取る戦略Xは「グーを40%、チョキを40%、パーを20%で出す」である。ピンとこなければ数値を代入してこの戦略に50%より高い勝率を出せる戦略がないことを確認してみるとよい。
では、最強デッキは存在せず、ナッシュ均衡点における戦略が存在するだけなのだろうか?メタ読みとはナッシュ均衡点を求めるだけなのだろうか?
そんなことはない。厳密なナッシュ均衡点を求めるにはゲームはあまりに複雑であり、人間は合理的な判断を取ろうにも完全に合理的にはなれないからだ。
次節では、コンピュータプログラムにより行ったシュミレーションからメタゲームとはどのような形で推移するものなのかに迫りたい。
以上の内容はどこのゲーム理論の本にも書いてありそうなことをかみ砕いて雑に紹介しただけである。以下が私が面白いと思って書いている内容だ。面白いと思うので面白がってくれ。
2. メタゲーム推移の本質に迫る
メタゲームはナッシュ均衡点に向かって収束していくのであろうか。答えはNO。結論から言えばメタゲームは振動する。デッキ使用率はナッシュ均衡点から上に引っ張られれば、使用率は下がり始める。しかしナッシュ均衡点にある使用率を飛び越えて次は下へ飛び出す。まるで、ひっぱったバネが元の長さに戻っても止まらずに縮むように。
初期値依存性
実際のゲームではプレイヤーはナッシュ均衡点を目指すのではなく、その瞬間で勝てる点を目指す。一度ナッシュ均衡に到達してしまえばデッキを変更するインセンティブは存在しなくなるが、ナッシュ均衡での戦略から離れた戦略からスタートしたらどうか?
TCGで3すくみが生まれるときにどのような過程で生まれるだろうか?次のようなケースは多いのではないだろうか。
①強いデッキA, Bが開発される。AはBに有利とわかりBは使われなくなる。
②Aが強すぎるのでAに有利なピンポイントメタデッキCが開発される。ただし、CはピンポイントメタデッキなのでBに不利である。
経験があるのではないだろうか。例えば私の経験では、チャレンジャーズガントレットでイゼットコントロールをプレイしたとき、AがウィノータでBがスゥルタイ根本原理、イゼットコントロールがCというのに近い状態であった。
このような場合ではすべてのプレイヤーがデッキAを使っている状態からメタゲームの推移が始まる。

次のような設定で実験を行う。
①存在するデッキは3つ、AはB、BはC、CはAに有利とし、有利さは等しいとする(じゃんけんと同じ)。
②ある時刻t+1で9割のプレイヤーはtと同じ戦略を取る。残りの1割のプレイヤーはtで最も高い勝率を得られた戦略を取る。
③t=0の時点ではすべてのプレイヤーがデッキAを選択しているものとする。
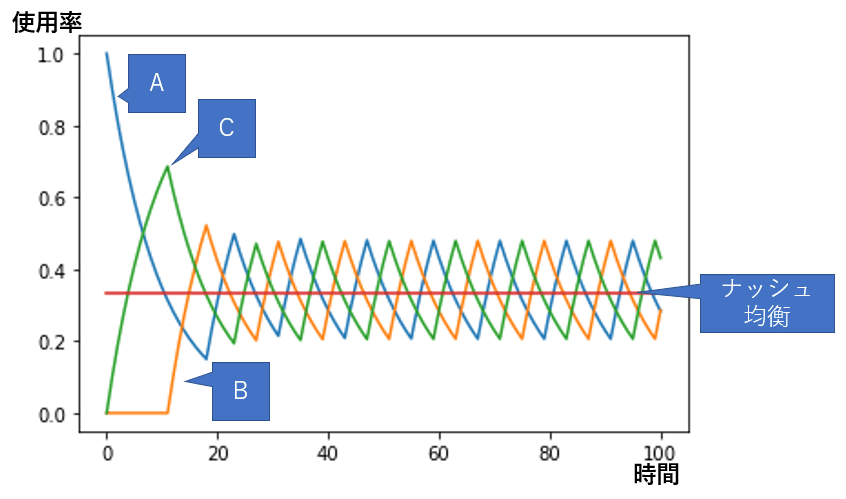
図はデッキA、B、Cの使用率をプロットしたものである。
ある程度はナッシュ均衡にメタゲームは近づく。しかし、収束することはなくナッシュ均衡点を中心に振動を続けることがわかる。
メタゲームの摂動
上の実験ではこんな反論があるかもしれない。現実ではこんなに規則正しく同じことが繰り返すなんてことはありえない。一度ナッシュ均衡に達すればプレイヤーには戦略を変更するインセンティブは働かなくなるので振動は止まるのではないか、と。
では実験に不規則性を加えてみよう。
次のような設定で実験を行う。
①存在するデッキは3つ、AはB、BはC、CはAに有利とし、有利さは等しいとする(じゃんけんと同じ)。
②ある時刻t+1で8割のプレイヤーはtと同じ戦略を取る。1割のプレイヤーはtで最も高い勝率を得られた戦略を取る。1割のプレイヤーのデッキ使用率分布はランダムである。(一様分布からサンプリング)
③t=0の時点ではすべてのプレイヤーがデッキAを選択しているものとする。
さきほどの実験の動かなかった9割のプレイヤーから、全体で見た1割がランダムに動くというモデルである。ランダムな摂動はプレイヤーの不合理性など様々な要因によりありうるだろう。

ランダム性により形は綺麗ではなくなっているものの、完全に不規則ではなく、やはりナッシュ均衡点を中心に行き来しているように見える。すこしゴチャゴチャしていて見づらいので、Aの使用率だけを取り出してみる。

ランダム要素のない実験では初期値が偏っているために振動が生じていた。ランダム要素があれば初期値が仮にナッシュ均衡点にあっても振動は起きるのだろうか?
同じ実験を初期値がナッシュ均衡の状態、つまり3つのデッキが等確率で使用されるという条件でやってみる。

見づらいので同じく一つ取り出してみる。

やはり、小さなゆれから始まって大きな振動になっていく様子が観察できる。
以上の実験を以って、メタゲームの推移の基本はナッシュ均衡を中心とした振動であると結論付けて終わりとしたい。
ナッシュ均衡点にないということは、戦略の取り方により50%を超える有利を取ることができることを意味する。また、全くの不規則ではない推移はメタ読みという行為の実現可能性を示している。
終わりに
あなたがこの記事を役に立つと思ったかしょうもないと思ったかはわからない。また、これだけ単純化したモデルでメタゲームの本質を語ろうなどとは烏滸がましいと思う読者もいることだろう。現実には、一つ先を読むプレイヤー、もう一つ先を読むプレイヤー、またモデルにない動きも存在する。
しかしながら、物事の本質を解明するために、きわめて単純化したモデルから始めることは重要である。初等力学が体積を持たず質量だけをもつ質点という仮想の単純化されたものの運動の記述からはじまるように。本記事が質点の運動の記述とまではいかなくとも、読者が質点の運動を考えるきっかけとなれば幸いである。
Appendix. 追加の実験データ
ランダム性のある実験であったので、記事を書くのに都合のよいデータを取り出してるのではないか、と言われないようにもう5回ずつやっておく。
それでも不十分だと思う読者は、簡単なシミュレーションなので自分でプログラムを書いてやってみるとよい。
初期値 (1,0,0)

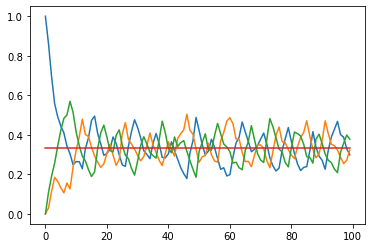



初期値 (1/3,1/3,1/3)





いいなと思ったら応援しよう!

