
へやわけのへや外周に対するペナルティの考え方
外周の黒マス数に対して考察
tobo定理っていうのがあるらしいけど、読んでないから同じこと書いてるかも
部屋周辺における白マスの塊の数と外部への余裕
部屋周辺における白マスの塊の数を考えていきます。
ここでいう白マスの塊の数とは下図のように、緑で囲まれたところに存在する塊の数のことで、実際の白マスの塊の数とは異なります。
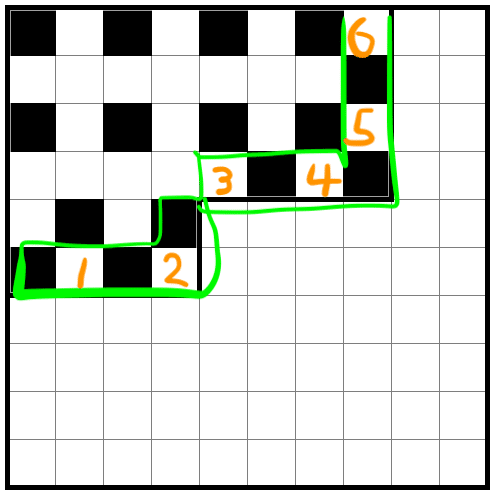

上記の図では部屋内部の白マスの塊の数は2ですが、部屋周辺における白マスの塊の数は6です。ここを混同しないように気をつけてください。
以後、境界線に接するマスのことを周辺のマスといいます。

この塊の数を式で表すと次のようになります。
部屋周辺の白マスの塊の数=周辺の黒マス数-端にある黒マス数-凹にある黒マスのセット数+頂点に接する黒マス+1

上記の図だと
端にある黒マス数=赤色の2マス
凹みにある黒マスのセット数=オレンジのどちらにも黒マスが入っている数
頂点に接する黒マス数=緑のマス
となるので、今回だと
部屋周辺の白マスの塊の数 = 6-1-0-0+1=6より、境界線付近での白マスの塊の数は6個となる。
ここで、余裕値R=周辺の白マス数-周辺の白マスの塊の数と定義します。
すると、余裕値Rは周辺の白マスの塊の数を減らさずに、配置できる黒マス数の基準になります。
例えば先ほどの図だと6-6=0となります。
余裕値の消費の仕方
次にこの余裕値Rがどのように消費されるかについて考えます。
これも次の図で考えていきます。
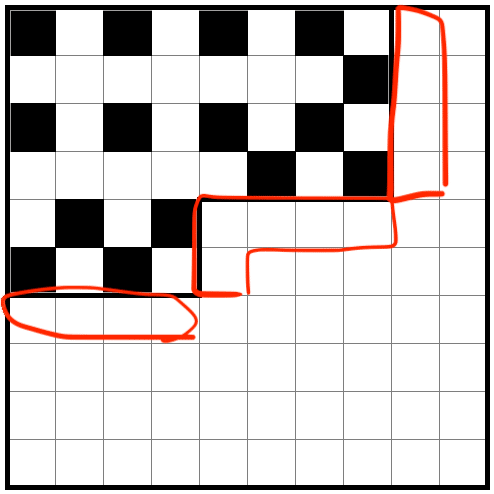
赤色のところを外部のマスといいます。
この時、余裕値Rは次のように消費されます。
余裕値の消費数I=赤色の黒マス数+青色のセット数+緑の黒マス数x2

仮に、下のように埋めると消費数Iは3+1+0=4となります。

例その1
これを次の図で考えていきます。

この時、部屋周辺の白マスの塊の数=5-2-0-0+1=4
余裕値R=7-4=3
となる。
また上記のように黒マスを配置すると、
消費数I=2+1+0x2=3
となる、よって
R-I = 3-3=0となる。
つまり、R-I =0ということは、これ以上消費数が大きくするような黒マスの配置ができないことがわかる。
例その2

上記の図だと、
塊の数=6、R=6-6=0、I=4なので、R-I=-4となります。
これが意味するのは、実際の部屋内部の塊数が、部屋周辺の塊数よりも4小さくなるということです。
実際に上の図では、部屋周辺の塊数=6、部屋内部の塊数=2というふうに4小さくなっています。これは部屋周辺の塊数が内部でつながることで、部屋内部の塊数を減らしています。
ここで、部屋内部の白マスの塊数は必ず1より大きくなります。つまり、
R -I >= 1-部屋周辺の白マスの塊数
が成り立ちます。これを利用すると、外部における黒マス数の上限が予想つきます。
ペナルティ理論との関係
この前自分が導いたペナルティ理論は次のようなものでした。
全体の辺の数(白-壁も含む)-4x黒マスの数-白マスの数-A_all+A_blackMAX = A_penalty + (白マスの2x2+白マスループ) - 部屋内部の白マスの塊の数
この、部屋内部の白マスの塊の数に上記の話が関わってきます。
外部に黒マスを置くと、消費数Rがどんどん大きくなっていくので、いつかR-I>= 1-部屋周辺の白マスの塊数の関係を満たさなくなります。その上限が外部に配置でできる黒マスの数です。
この数について、部屋周辺(最初に決めた緑のところ)に置かれる黒マスをN個と指定した状態で消費数の最大値を計算してみます。ただし、岬のマスはないと仮定します(ややこしいから)
今、以下のように記号を決めます。
周辺に置かれなかった黒マス数=P1
角に置かれなかった黒マス数=P2
岬に置かれなかった黒マス数=P3=0
(A_penaltyを3つに分けた)
また、全体の辺の数(白-壁も含む)-4x黒マスの数-白マスの数-A_all+A_blackMAX =Zとします。
すると、
Z=P1+P2+ (白マスの2x2+白マスループ) - 部屋内部の白マスの塊の数
また、
R=外周の白マス数 - (外周の黒マス数-端にある黒マス数-凹にある黒マスのセット数+頂点に接する黒マス+1)
R-I >= -部屋内部の白マスの塊の数+1
となる。
よってまとめると
外周の白マス数 - (外周の黒マス数-端にある黒マス数-凹にある黒マスのセット数+頂点に接する黒マス+1) + Z -(P1+P2+ (白マスの2x2+白マスループ))- 1 >= I
となる。この左辺の最大値がわかれば、部屋外部における黒マスの最大値がわかる。
左辺のうち変数部分は
- (外周の黒マス数-端にある黒マス数-凹にある黒マスのセット数+頂点に接する黒マス) - (P1+P2+ (白マスの2x2+白マスループ))
となる。
つまり、
大きくした方がいい:端にある黒マス数、凹にある黒マスのセット数
小さくした方がいい:外周の黒マス数、頂点に接する黒マス、P1+P2+ (白マスの2x2+白マスループ)
今回は外周の黒マス数は固定で考えているので除外
端にあたる黒マスについて考える。
辺にある黒マスを端に移すことを考えると
P2は-1、端にある黒マスは+1となるので、Iに特に影響は与えない。
また、(白マスの2x2+白マスループ)に関しては0を仮定して考える。
辺にある黒マス2つを凹にある黒マスのセット数に移すことを考えると、(隣接禁を考慮しなければ)1得することになる。
つまり、黒マスはできるだけ、凹にある黒マスのセット数に配置した方が良い
頂点接する黒マスはできるだけ小さくした方がいいので、外周における数が決まってるなら置かないほうがいい
という感じで消費数の最大値の目安みたいなものは出る。ただ、当然外部への影響を減らすということは、内部への負担が大きくすることにつながるので、後半の
凹にある黒マスのセット数、頂点接する黒マスの議論は場合によります。
ただし、消費数を最大化しても、外部における黒マスが最大化されるとは限らない。
なぜなら、余裕値の消費数I=赤色の黒マス数+青色のセット数+緑の黒マス数x2
というふうに場所ごとに傾斜があるので、特に青色のセット数に影響が出る可能性がある。
端以外の角に黒マスをおくと、Rは大きくなるが青色部分の配置数が1つ減るので、配置数には影響を与えない。
これ以上はまとめ方がわからんけど、ざっくりと外部に配置できる黒マスの最大値を知る方法でした。実際は隣接禁が影響するからもっとごちゃごちゃなはず。
