
解説 しろまるくろまる1 ハバネロ
4回修正して再投稿しまくった問題、Notmilkさんのソルバーを借りてなんとか作りました。
結論、境界線の出入り口を決めてあげると解けます。
前提知識:境界線の制約
しろまるくろまるの基本手筋である、市松禁や外周の白丸と黒丸がひと繋がりにならないといけないというものは省略します。
しろまるくろまるは2x2禁があるので、境界線がすべての内部頂点を通る必要があります。なので、内部頂点の市松をとってあげることで、出入り口に制限がかかります。

上の図だと、赤から入って赤から出ないといけないので、出入り口に制限がかかっていることがわかります。
今回は盤面を次のように塗り分けます。今回は赤から1つ、青から1つ出る必要があります。

この問題の解説
この問題の肝はこの境界線の引ける場所に強い制約がかかっているということでした。実際に見ていきます。
上部の白丸が破綻することの証明
まず、次のように白丸を2つ追加した盤面について考えていきます。

すると、上部の4つの塊で、青い点から境界線が出ることがわかります。なぜなら、出ないと仮定すると、破綻するからです。

(下の白丸が抜けてます)
以上から、他の点では、青い点から境界線が出てはいけないことがわかります。
すると、次のピンクで囲まれたとこでは色が一致することがわかります。

その中でも、特に下図の緑のところを考えると、ここは4つとも黒の場合しかありえないことがわかります。

つまり、ここまで確定します。

すると、次に以下の場所を白丸で仮定すると破綻することがわかります。

そして、これは同様の議論で端っこまで波及します。

同様に右も考えると次のようになります。これは、最初の内部頂点の市松の議論を考えると破綻していることがわかります。


ということは、最初の白丸の仮定に問題があります。なので、次は、上部の白丸を黒丸として解いてみます。
下部の白丸が破綻することの証明

ここで、さっきのようにピンクの部分で白丸黒丸が一致すると仮定します。

すると、さっきと同じように進んで、破綻することがわかります。

よって、先ほど仮定したピンク部分のどこかから出入りすることが確定するので、上部の青頂点からは出入りしないことが確定する。よって、次のように決まります。
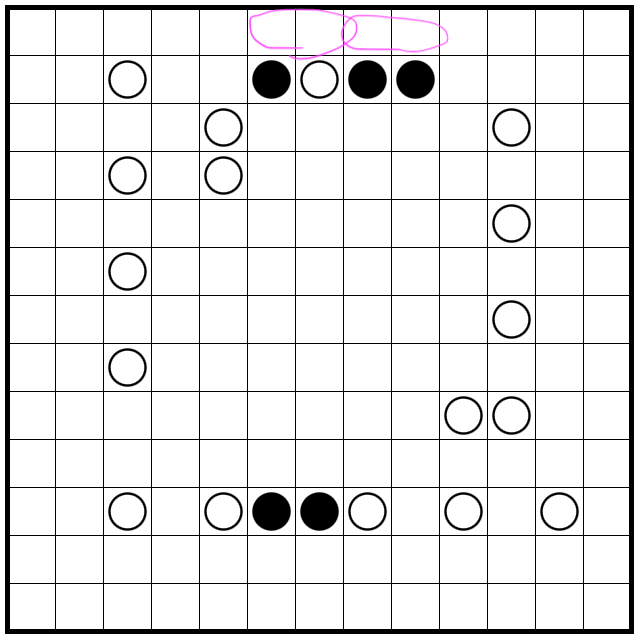
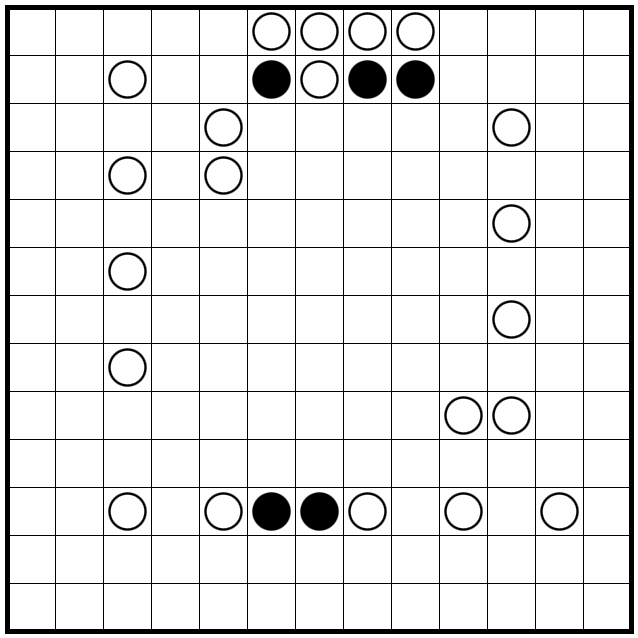
次に、残りの外周を2つに分けて考えていきます。

まず、右側の青色の部分について考えていきます。
先ほどと同じようにピンクの部分で一致することを仮定すると、破綻することがわかります。




同様に左の青色側でも同じようになるので、赤色側も青色側も青の内部頂点から線出入りすることが確定します。よって、破綻します。
以上から、最初の下側の白丸を仮定したことが間違いだったことが確定します。

あとは、この黒丸の時の解があればOKです。

ありました。よって、正解はこの黒丸でした。
また、コメントに書いてある2つ決まったというのは、次の2つです。

ただ、この白丸は想定していなかったものなので、なぜ決まるのかあまりわかっていないです。
ということで、ハバネロしろまるくろまるの解説でした。
ソルバー提供してくださったNotmilkさんありがとうございました。
