高校数学 三角比(三角関数) #1

リュディアです。高校生の皆さん向けの三角比、一部三角関数を含む解説です。1年生の数学の中では1つの山場ですよね。三角比で数学が嫌いになった、あるいは物理の力学でも三角比が出てきていわゆる理数系への進学は諦めたという方も多いと思います。

私が思うに学校の授業の三角比はやたらと覚えないとダメなことが多いのが問題だと思います。入試対策と割り切ると覚えていないと試験の時間が足りないことも多々あるのですけどそれにしても覚えることが多すぎるとしんどいですよね。覚えることは最低限にして頭にイメージを浮かべて学習していくといいと思います。

実際、アニメやドラマで「サイン、コサイン、タンジェント！」というセリフがあるくらい、難しい数学の代名詞として使われている現実もあるので気持ちはわかります。でもしっかりとやりなおせば一週間で十分に取り返せます。頑張ってみましょう。

さっそくですが三角比（三角関数）と書いたのはなぜかというと1年生の間は0~180度までの範囲しか扱わない、つまり三角形の内角の和なので三角比です。180度以上の範囲を扱えるように拡張したのが三角関数となります。ここでは理解を深めるために高校1年の数学を逸脱した内容も使います。でも心配は不要です。丁寧に解説しますので読んでください。

三角比では直角三角形を扱います。これは重要なことで、例えば複雑な問題が出てきても直角三角形に分割すればとける場合が多いと言えます。では最初に次の直角三角形を見てください。

三角形ABCは直角三角形です。角Cの大きさは直角ですが各Bの大きさはθ（シータ）です。ちなみに角の向かい側のa, b, c は辺の名前あるいは長さです。角Aの対辺の名前あるいは長さを a とするのは数学の慣例ですから皆さんも意識してください。ここで三角関数を扱うときには直角を右下、三角比を求めたい角が左下になるよう配置します。上の図も直角Cが右下、三角比を求めたい角Bが左下に配置しました。この状態で sin / サイン、cos / コサイン、tan / タンジェントは次のように定義されます。

これは定義なので覚えるしかないのですが、昔から伝統的な覚え方があります。今は中学でアルファベットの筆記体を学ばないので難しいかもしれないですが、ここだけお付き合いください。まず sin からいきます。三角形ABCの上で大文字の Sを筆記体で書くと辺 c, 辺b の順になぞることになります。だから b/c になると覚えてください。下の図を見て自分でなぞってみてください。

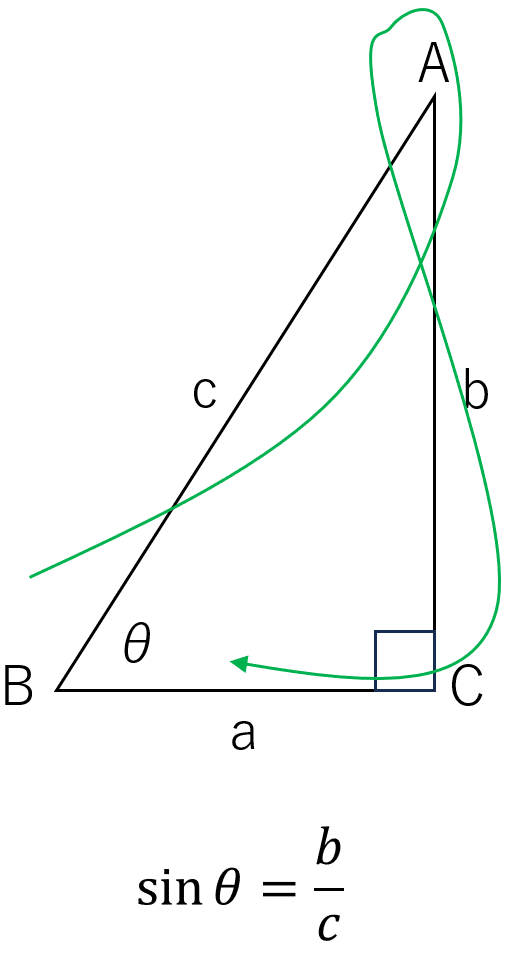
同様に cos は Cなので大文字、小文字は関係ないですが三角形ABCの上でなぞると辺c、辺a の順になぞることになります。だから a/c になると覚えてください。これも下に図をつけておきます。

最後に tan は 小文字の tになります。三角形ABCの上でなぞると辺a、辺bの順になぞることになります。だから b/a になると覚えてください。これも下に図をつけます。

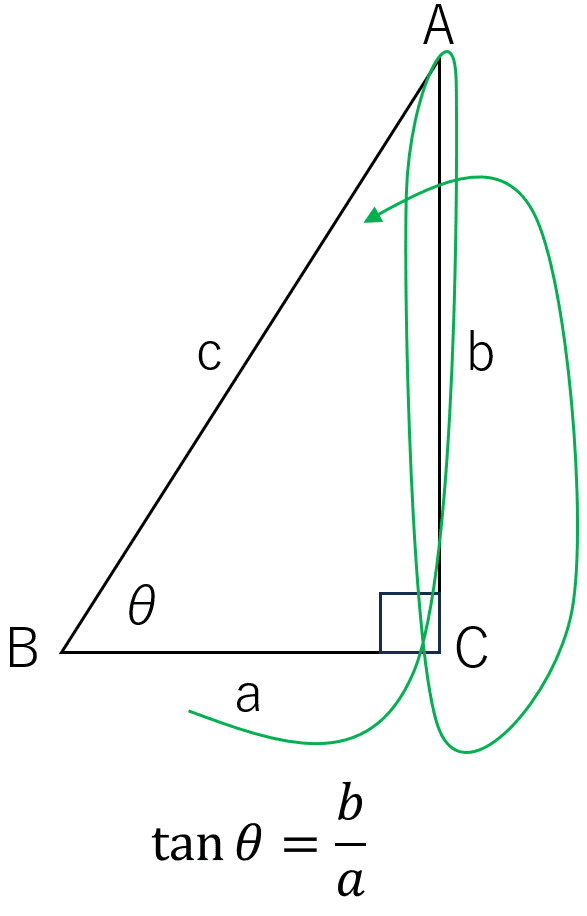
これで sin, cos, tan の式は暗記できましたか？暗記というか語呂合わせというか、単に覚えるよりは頭に残りやすいと思います。再度の注意事項は直角三角形の直角を右下、三角比を求めたい角を左下になるよう配置し、その状態で上の規則でsin, cos, tan を式で表してください。これで間違えることはありません。

今回は導入だけになりましたが、しっかりと理解してください。

では、ごきげんよう。