G検定 k-近傍法とk-平均法

株式会社リュディアです。G検定対策として混乱しやすい k nearest neighbor （k 近傍法）と k-means（k 平均法）についてまとめてみます。

いずれも機械学習の1手法です。k がついているので混乱しますが k は単に k 個を意味するものです。混乱しやすい、ということは G検定でも問われることが多いので区別できるようにしておいてください。

k近傍法（k nearest neighbor）

k はハイパーパラメータです。つまり人間が決める必要のある数字です。k は多数決をとることを考えて一般的に奇数を用います。以下の図をみてください。

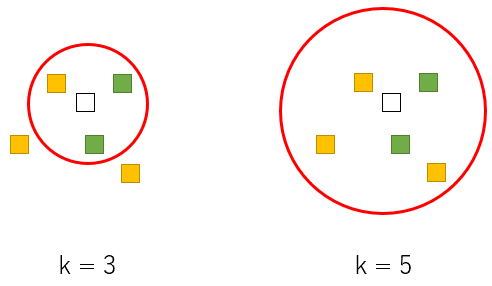
今、白の四角を分類したいとします。k = 3 なので白を中心として近い点を 3 つ選択します。近いというのはこの絵では距離が近いことになりますが、実際の問題では近さを定義する必要があります。赤丸で囲った中に k = 3 の四角が入っており、これが最近傍の 3 点となります。緑が 2 つ、黄色が 1 つですので白の四角は多数決で緑に分類されます。同様に k = 5 の場合は黄色が多くなるので黄に分類されます。

k 近傍法はあらかじめ黄や緑といった教師データが与えられているので教師あり学習の 1 手法です。またあらかじめ色の情報が与えられているのでクラス分類を扱う機械学習の方法になります。

k平均法（k-means）

k平均法は教師無し学習の 1 手法でクラスタリングに適した方法です。k nearest neighbor （k近傍法）で出てきたクラス分類と、ここで出てくるクラスタリングで混乱している方は以前にまとめたクラス分類とクラスタリングを事前に一読してください。

では k平均法についてまとめていきます。教師無し学習の1手法であるためあらかじめ与えらえる情報はありません。動作は以下のようになります。以下の図をみてください。6個の青い点があります。

この点をまず適当に 3 個ずつに分類します。分類がわかるように黄グループと緑グループとして色をつけました。

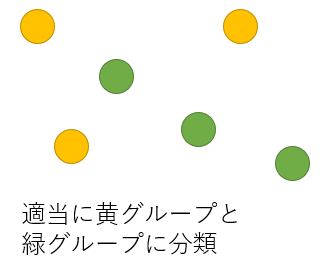
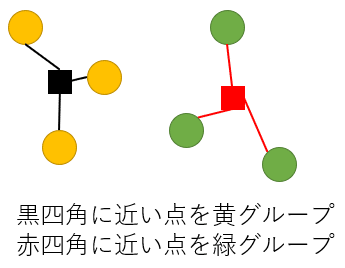
黄グループどうしで重心をとり黒の四角、緑グループで重心をとり赤の四角としました。

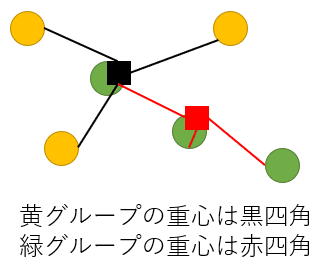
ここで黄色、緑色という元の色は無視して2つの重心に近い点をそれぞれ 3 つずつ選択しなおします。すると黄グループ、緑グループは以下のようになります。

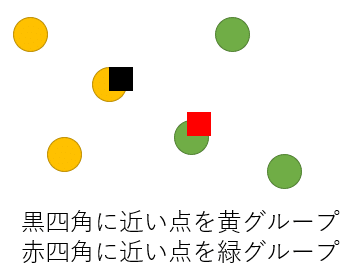
新しくできた黄色グループ、緑グループで再度重心を考えるときれいに2つにわかれました。今回は 2 回でうまくわかれましたが実際には収束するまで本手法を繰り返します。

具体的なイメージを持ってもらえましたでしょうか？再度にもう一度まとめておきます。

k近傍法（k nearest neighbor）は教師あり学習でクラス分類に適用します。k平均法（k-means）は教師無し学習でクラスタリングに適用します。

では、ごきげんよう。