H31 (R1)年度 全国学力テストで統計量を扱う #3
株式会社リュディアです。今回は公開されている H31(R1)年度 全国学力テストの情報を使って回帰分析についてまとめてみます。
まず回帰分析について説明します。2 つの変数 x, y があるとき変数 y の変化を変数 x の変化で説明可能かどうかを検討するための手法です。
説明したい変数 y を目的変数、予測に使う変数 x を説明変数とよびます。今回は単回帰分析を扱うので説明変数は x のみ、つまり 1 つです。複数の説明変数を扱う場合は重回帰分析と呼びます。こちらについてはまた別途まとめます。
単回帰分析、特に線形単回帰分析では目的変数を y = ax + b で表現できると仮定し入力データを元に a, b を決め、x から y を予測するモデルをたてます。
今回はH31(R1)年度全国学力テストに参加した中学校、小学校の学校数と生徒数の間に関係があるかどうかを検討するための単回帰分析を行います。生徒数が多いと学校数が多いのでは、という予測が妥当かどうかを検討することになります。
まず元データとなる都道府県別の学校数と生徒数、さらに生徒数 / 学校数、つまり学校あたりの平均生徒数をまとめた表を以下につけます。まずこの表を見たときに気づくことは神奈川県での学校あたりの平均生徒数が突出して大きいことです。いいのか悪いのかはわかりませんが平均値で見る限り神奈川県では 1 つの学校が抱える生徒数が多いということです。

ではこの表を元に中学校、小学校のぞれぞれに対し学校数と生徒数に関する回帰分析を行ってみます。Excel を使って単回帰分析を行いますので以下に操作方法も記載します。
まず Excel で散布図を描いてみてください。例として中学生の学校数と生徒数の散布図を描くと以下のようになります。横軸が生徒数、縦軸が学校数です。

次にグラフ上の点をクリックしてデータを選択した状態で右クリックでメニューを表示すると以下のようになります。

この状態で近似曲線の追加を選択すると以下のようなメニューが表示されます。

今回は直線で近似しますので線形近似を選択、さらにグラフ中に y = ax + b の数式と R2 を表示したいので2箇所を✔します。ここまで処理すると以下のような散布図が得られます。小学校についても同様に処理してください。以下のような散布図がえられましたか?
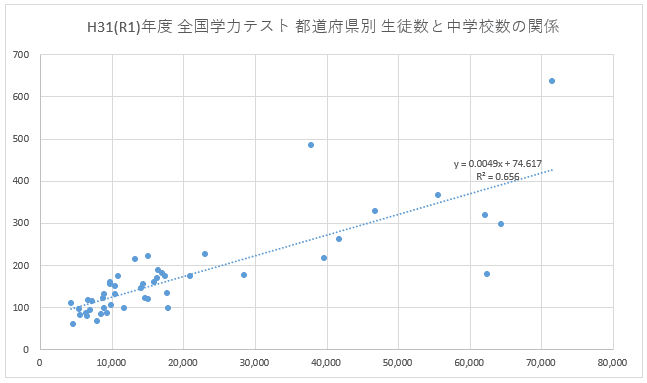

散布図の中に y = ax + b で表現された数式も出ていますね。これが回帰分析結果です。また R2 (厳密には R の右上に 2 )も記載されています。この R2 を決定係数と呼びます。推定された式がどの程度元データに当てはまっているかを表し 0 ~ 1 の数をとります。1 に近いほど合致していることを示します。分析結果より中学校の R2 は 0.656、小学校の R2 は 0.707 です。目安として 0.6 以上であればそれなりに合致している、0.8 以上であればしっかりと合致していると考えてよいと思います。今回はいずれも 0.6 以上なのでそれなりに合致していると考えてよいと思います。

次に直線から大きく離れている点について調べてみます。中学校のデータを例としますが小学校についても同様に調べてみてください。推定された直線より下側が生徒数に対して学校数が少ない、直線から上側は生徒数に対して学校数が多いことを示します。神奈川県が突出して学校数が少なく、ついで愛知、大阪が少ないです。また東京は生徒数に対して学校が多いことになります。北海道は面積が大きいので別な要因があると予測できます。いわゆる三大都市圏で東京だけが生徒数に対して学校数が多く、それ以外の神奈川、愛知、大阪では生徒数に対して学校数が少ないという検討結果がえられました。
今回は生徒数と学校数の関係を回帰分析で検討してみました。これからもまとめの記事で回帰分析は使っていきますので徐々に慣れていってください。
では、ごきげんよう。
この記事が気に入ったらサポートをしてみませんか?
