【ランダム行列】MathematicaでWigner半円則を見てみよう
タイトルの通り、この記事ではMathematicaを用いてWigner半円則を見る。ただ確認にすぎないが、意外と日本語の情報が少ないので記した。同様の話題で書かれた記事もすでにあるにはあったが、それは本来Wigner半円則と呼ばれるものではなかったというか、私がほしかった情報ではなかったので、改めて本稿で紹介したいと思う。
Wigner半円則
これはランダム行列の理論で、ポテンシャルをGauss型に取ったときに現れる。行列サイズ$${L}$$を大きく取ったとき、その行列の固有値密度の分布が半円状になるというものである。つまり、
$$
\displaystyle \mathcal{Z}=\int e^{-L\mathrm{Tr} V(H)} dH
$$
のような行列積分でポテンシャルを
$$
\displaystyle V(H)=\frac{1}{2}H^{2}
$$
と取ったときに固有値密度が次の形で表される。
$$
\displaystyle \rho(x)=\begin{cases}
\displaystyle \frac{1}{2\pi}\sqrt{4-x^{2}} & (|x|<2)\\
0&(|x|>2) \end{cases}
$$
Mathematicaで実際に見る
ここではランダム行列$${H}$$をHermiteであるとする。
rndm = RandomVariate[GaussianUnitaryMatrixDistribution[Sqrt[1/L], L]]
eig = Eigenvalues[rndm]
Histogram[eig, {0.25}, "ProbabilityDensity"]これでGauss型のポテンシャルに従うサイズ$${L}$$のランダムHermite行列が生成され、固有値が評価される。これを幅0.25のヒストグラムで表しているが、このときオプションでProbabilityDensityを指定することで固有値の現れる確率密度を作ってくれる。
実際にいくつか確認してみた。
10次のとき
行列は$${10\times 10}$$であったとしても人の手には負えないので計算機にすべて任せる。しかし、このサイズはランダム行列の理論が想定する"大きいサイズ"では全くなく、むしろ小さくすらある。当然、目立った特徴は見られない。

50次のとき
多少端の方が縮んでいる。円に近づくか?と期待できる。

100次のとき
だいぶ規則性が見える。このくらいまでなれば半円と言っても文句は言われないだろう。

1000次のとき
ここまで来ると完全に半円則を満たしていると言える。

5000次のとき
念のためさらに大きいサイズでも確認してみた。紛れもなく半円である。

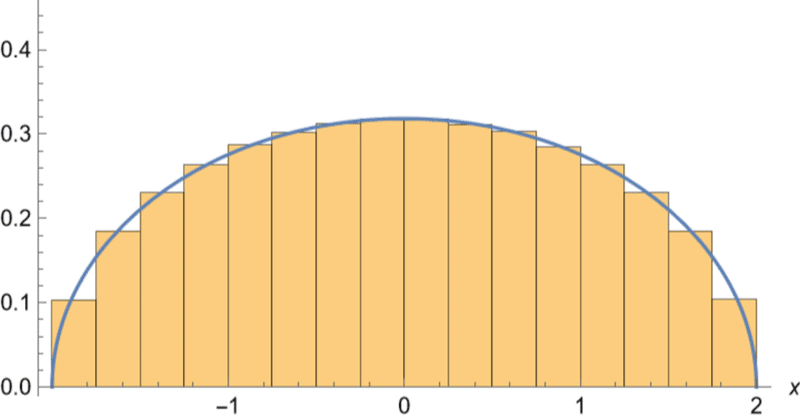
$${\rho(x)}$$のグラフも重ねて、実際に半円則を満たすことを確認する。気持ちいいくらい一致している。

まとめ
本稿では、計算機上でランダム行列を計算して固有値密度を評価することでWigner半円則が満たされることを確認した。普通に紙の上で計算する場合は「サイズ$${L}$$を大きく取る」と言って極限を取っていたが、実際に計算機で確認してみると$${L=100}$$程度でも半円状の分布を示しており、$${L=5000}$$ともなればほぼ半円に乗っていることがわかる。
おまけ: 10000次で幅を0.01に取った場合
計算機の性能が足りていないのでだいぶ時間がかかった。こちらの設定のほうが正確な計算が出来ているはずである。ただし幅を小さく取っているので当然またランダム性からくるゆらぎが見られる。サイズが小さいときに幅を小さく取りすぎるとその範囲に入る固有値がないことも多く出てくるので適切に振る舞いを確認できない。なので本編では0.25と取っている。

おまけ2: 10次から100次で半円に近づく様子の動画
$${L=10 \to 100}$$の変化を1刻みで動かした。このくらいでも収束(?)する様子を見ることができる。

参考文献
渡辺澄夫, 永尾太郎, 樺島洋介, 田中利幸, 中島伸一, ``ランダム行列の数理と科学,'' 森北出版, 2014.
入門的な内容が載っている。どちらかというとランダム行列の紹介という感じの本ではあるが、内容は200ページに満たない中で必須の知識は学べる上に、応用範囲についても簡潔に述べられているため手にとって損はない。この記事のモチベーションの1つには、本書の図2.1を再現したいというものもあった。
木村太郎, ``ランダム行列の数理,'' 森北出版, 2021.
ランダム行列について基礎知識から発展的内容まで載っており、最新の研究成果にまで言及している。本編だけで300ページを超え、日本語の書籍ではこれが一番充実していると思う。
Bertrand Eynard, Taro Kimura, Sylvain Ribault, ``Random matrices,'' arXiv:1510.04430[math-ph]
「ランダム行列の数理」の著者を含めた研究者らによる講義録。本論文の著者らは特に近年物理学への応用で注目されるような仕事を多くしている。こちらも入門編から発展編まで、詳細な内容が述べられているが、英語である。
この記事が気に入ったらサポートをしてみませんか?
