代数の公式を幾何的に理解する。

代数の公式は幾何としても説明できる。以下の公式
(a+b)(a-b)=a*a-b*b
が幾何的に成り立つことを説明する。
(a+b)(a-b)は幾何的には長方形の面積を表している。その長方形の一辺の長さが(a+b)、もう一辺の長さが(a-b)。これを図で表すと以下になる。

図１ (a+b)(a-b)の面積

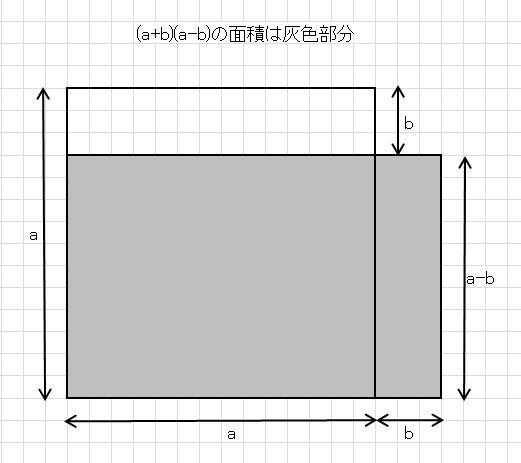
上図の右側の長方形をピンク色で示す。このピンクの長方形の面積はb(a-b)となる。

図２　ピンクの面積はb(a-b)

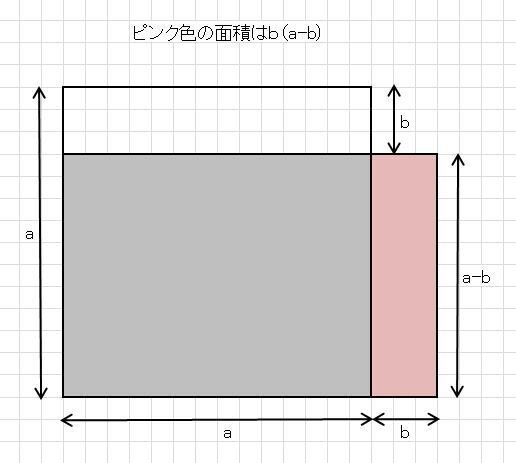
ピンク色の長方形の向きを９０度回転して、灰色の長方形の上に置くと下図になる。

図３　ピンク色を移動する

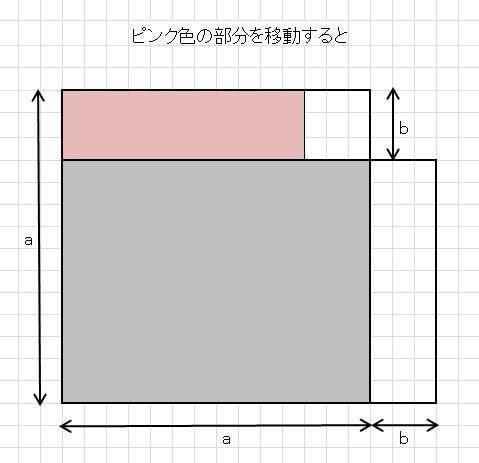
ピンク色の面積は、b(a-b)なので横の長さがa-bとなる。ピンクの右にある四角形の横の長さは、bとなり、高さもbなので正方形になる。この正方形の面積はb*b。

図４　灰色の面積

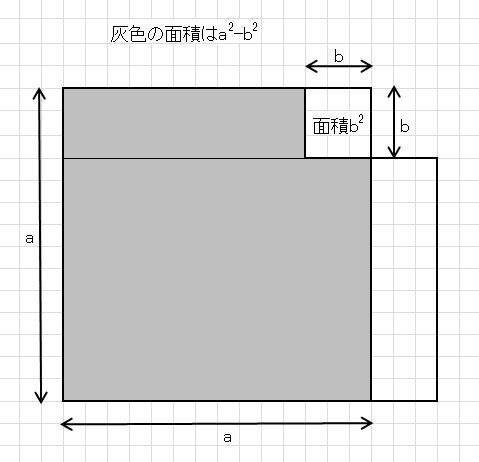
上図の灰色の面積は、a*a-b*bとなり、図１の灰色の面積と等しいので以下の式が成り立つ。
(a+b)(a-b)=a*a-b*b