
【小5:最小公倍数】かんたんに最小公倍数を求めるポイント解説(小5シリーズ⑤)
※この記事は、深澤英雄先生(神戸市の小・中学校で38年間教壇に立ち、教職大学院の特任教授を4年半務める。現在は和歌山大学教育学部の非常勤講師として学生の指導にあたる。久保田学園の第一号の生徒でもある。)をお招きして、久保田学園グループ代表久保田勤とグループ講師宮後のお話をベースに記事にしています。
前回の記事はこちら
全国テストから見る、子どもがつまずく最小公倍数
宮後:今回は最小公倍数について、お話を伺いたいと思います。深澤先生よろしくお願いします。
深澤:また全国学力テストからの引用になりますが、最小公倍数の問題については、2種類の問われ方があります。まず1つめを見てください。

深澤:この問題の答えは ”24”です。このように、最小公倍数を書きましょうと言われると、間違える人はとても少ないのです。学力テストでも実施されましたが、非常に高得点です。それでは、もう一つの問題を見てください。
A町行きのバスは8分おき、B町行きのバスは12分おき、午前8時に2台のバスが同時に発車しました。次に2台のバスが同時に出発するのは何時何分ですか。
深澤:このように出題出題されると、途端に正解率が下がってしまうのです。
久保田:この問題は、大人なら、「8・12」の”最小公倍数”を使えばよいとすぐわかりますが、この問題を間違った子どもは”最小公倍数を使えばよい”ということが分からなかったのだと思いますね。
書き出しを軽視しない!
深澤:私もそうだと思います。なぜ最小公倍数が使えるとわかるのか、やはりそこでは具体的に書き出してみることが大切だと思います。
A町行きのバスは8分おきなので、発車時刻は、
8:00 8:08 8:16 8:24 8:32・・・となります。
B町行きのバスは12分おきなので、発車時刻は、
8:00 8:12 8:24 8:36 8:48・・・となります。
宮後:結構大変ですね。ですが、このように書いてみると、時刻表が倍数に従っているのがわかりますね。
深澤:その通りですね。それぞれが8時ちょうどから図って何分後に発車しているかに注目すれば、もっとわかりやすいものになります。
A町行きのバスは8分おきなので、
8分後 16分後 24分後 32分後 40分後・・となります(8の倍数)。
B町行きのバスは12分おきなので、
12分後 24分後 36分後 48分後 60分後・・となります(12の倍数)。
深澤:このようにみて、同じ時間になる、つまり、8・12の倍数で共通の数字、公倍数を求めればよいということがわかるのです。
久保田:今回のように、具体的に書き出してみて規則性・法則を見つける、その上でならった計算方法を当てはめるというのはとても大切な事です。大学入試の数学でもレベルは違っても同様の作業をします。この具体的に書きだすというのはずっと使える技術だと思いますね。
ミスが大幅に減る簡単な最小公倍数の求め方
宮後:とはいえ、”8・12”の最小公倍数を求めるということ自体がなかなか難しいのではと思います。私自身も小学生の頃は、全部掛け算して、なんとなく調整するようなやり方をしてましたね。”8×12=96だと大きすぎるから、半分にして48だと・・・もっといけそう24くらいかな?とかなりあてずっぽうにやってましたね。
深澤:皆さんそうだと思います。学校の現場でも倍数を書き出して、共通のものを探すというのをやっていますね。
8の倍数 8 16 24 32 40 48 56 64 72
12の倍数 12 24 36 48 60 72 84 96 108
宮後:このやり方だと、計算間違いや見落としをしていないか心配になるんですよ。実際に、書き出した後に「もっと小さい最小公倍数があった!」と後で間違いに気付くこともよくありました。
深澤:これは子どもだけでなく、宿題を見てあげる保護者の方も良く悩んでいるようです。子育て関連悩みキーワードでも「最小公倍数の簡単な求め方」が上位にありましたね。

深澤:今回は、見落としや計算ミスが少なくなる”最小公倍数の求め方”をご紹介したいと思います。ところで、最小公倍数を求めるとき、要するに”何倍すればちょうど同じ数字になるか”がポイントになりますよね。
宮後:そうですね。さっきの”8と12”の場合だと、8×3=24・12×2=24 この”
×3 ・ ×2 ”を見つけるのが最小公倍数のポイントだと思います。
深澤:この”×いくら?”を簡単に見つける方法を説明します。8や12がどのような掛け算で表現されるかに注目しているんです。8は掛け算で表現すると2×2×2=8 と表現されますよね。
宮後:そうですね。同様に12は、2×2×3=12と表せることができますね。
深澤:この 2×2×2 と 2×2×3 の共通部分と違う部分に注目してほしいんです。2×2×2 2×2×3 共通部分は 2×2 違う部分としては8には×2が、12にはそれに×3があるわけなんです。

宮後:同じ数字にするためには、お互いに足りない数字を掛け算すればよいということですね。こうしてみると、上の図で最初に見せていただいた計算部分は共通部分と足りない部分を見つけ出すためにやっていることなのですね。
深澤:下の図のように書き出してみてください。
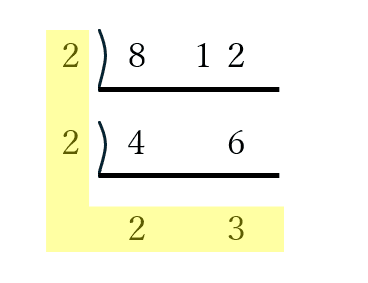
深澤:この黄色のL字の部分を掛け算して2×2×2×3で24と計算するのです。手順は次のようになります。
①数字を横に並べる
②全ての数字も割り切れる2以上の数字を左に書き、その数字で割ったときの商をそれぞれの下に書く
③どの組も互いに共通の約数が1以外なくなるまで続ける
④外側L字状に並んだ数字をすべてかける
宮後:12と30でもやってみましたが、簡単にできますね。2×3×2×5=60ですね。
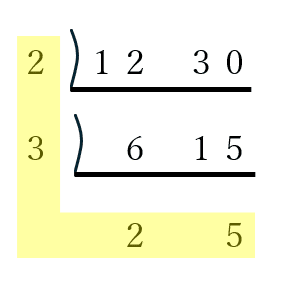
久保田:このやり方は”連除法”という方法で、中学校でならう素因数分解の内容が含まれるので、小学校では習わないかもしれません。ですが、小学生でもわかりやすい上に、掛け算・割り算の成り立ちの根本を含んでいるので今学んでいても将来に役立つ良い方法だと思います。
深澤:ぜひ最小公倍数を求める練習をしてほしいですね。ここをマスターして最小公倍数を学んでいると、分数の足し算・引き算の通分で躓かなくなるのでとても大事な部分だと思いますね。
まとめ
‣計算はできても、最小公倍数をどう使うかを見分けることを苦手とする子どもが多い
‣具体的に書きだす事が効果的。公倍数だけでなく、算数・数学の基本!
‣連除法がわかると、公倍数で躓かなくなる!分数の足し算・引き算も安心
