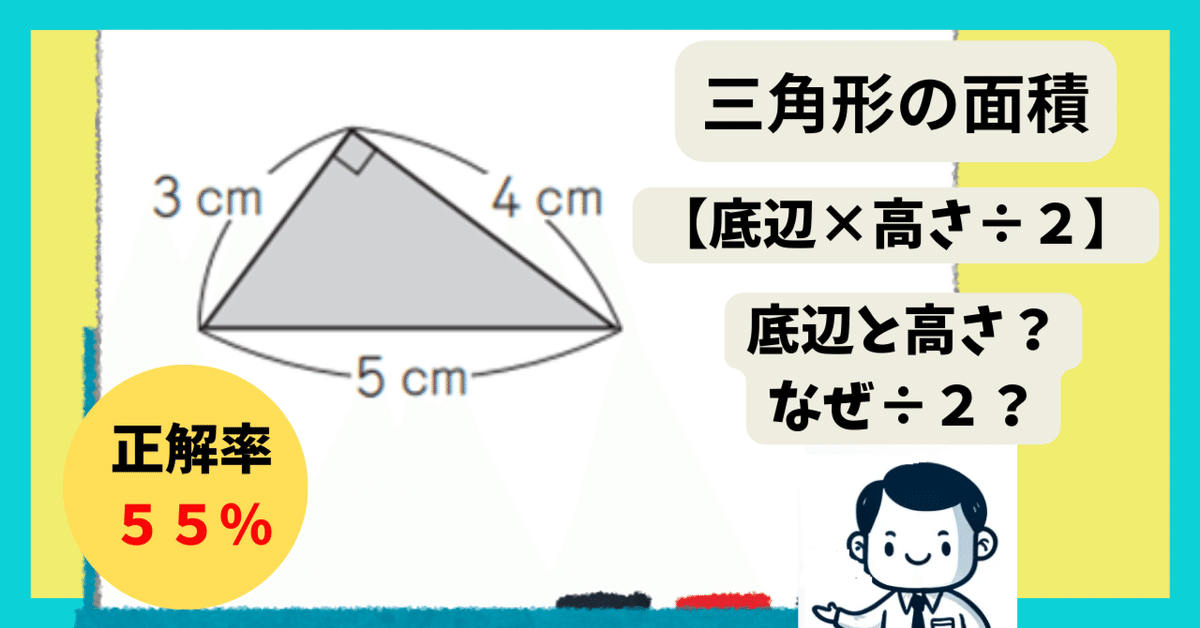
【小5:三角形の面積】一言でわかる!子どもが図形を理解しているか、確認する方法を教えます!(小5シリーズ③)
※この記事は、深澤英雄先生(神戸市の小・中学校で38年間教壇に立ち、教職大学院の特任教授を4年半務める。現在は和歌山大学教育学部の非常勤講師として学生の指導にあたる。久保田学園の元生徒で生徒第1号でもある)をお招きして、久保田学園グループ代表久保田勤とグループ講師宮後のお話をベースに記事にしています。 ※前回の記事はこちら
宮後:今回は、小5の勉強で詰まりやすい部分をどう乗り越えるかというテーマで、三角形の面積の求め方を例に挙げてお話いただくということで、深澤先生よろしくお願いします。
深澤:よろしくお願いします。三角形を例に挙げた理由は、小学校6年生を対象にした2021年に実施された学力テストの結果の事をまず皆さんにお伝えしたいからです。実はこの問題の正解率が55%しかなかったんです。
久保田:これは、教育業界で大変な驚きをもって受け止められましたね。これは小学校の段階ですでに図形が嫌いになってしまった子どもの数を表しているように思えてしまって私もショックでした。算数を手順で捉えてしまって、考え方が分かっていないことが顕著に示されている事例だと思います。
深澤:『三角形の面積は、「底辺×高さ÷2」でしょ。なんでこんな簡単な問題ができないの?』と思われる保護者の方もおられると思います。正答できなかった多くの子どもは、この問題を解くために必要な「底辺と高さ」がどこにあるのかを見つけられなかったようです。なぜこのようなことが起こるかというと、単純に数字だけ見て計算してしまうクセがついてしまっていたからだと考えられます。教科書やワークには下のような問題が多く出題されています。
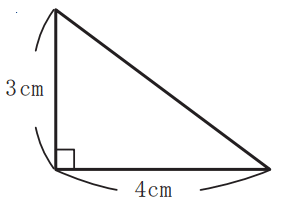
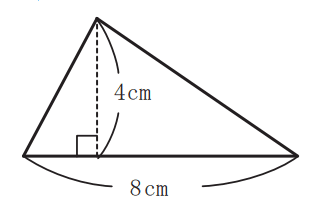
久保田:子どもが宿題をしていて、4×3÷2、8×4÷2と正解していても、考え方が身についているかよく見てあげて欲しいです。問題に書いてある、数字だけを見て計算するクセがついている可能性があるかもしれません。その状態だと、子どもが学力テストのような問題に躓いているかもしれません。

深澤:学力テストでは、5×3÷2、5×4÷2といった間違いが多かったようです。中には、5×3÷4といったものまであったようですね。子どもの中に”とにかく、掛け算して、2で割るんだ”という手順だけをなんとなく覚えている状態の子どもがたくさんいたことが学力テストの結果わかると思います。
垂直をイメージできているか
久保田:三角形の面積の公式【底辺×高さ÷2】という公式を暗記するのは難しいことではありません。ですが意味を含めてしっかり理解するのには少し壁があるということだと思います。図形はかなり抽象度が高い分野です。子どもが頭の中に具体的なイメージを持てるようにしてあげたいとおもいますね。そもそも底辺・高さという言葉も少し分かりにくく、急に出てきて戸惑う子どももいるのではないかと思います。
深澤:正方形や長方形の面積を習う時は【横×縦】と習います。それが三角形になると、急に【底辺×高さ】という言葉になります。底辺・高さという言葉を理解しようと思うと、ここで具体的なイメージが浮かぶものにしておくといいですね。
宮後:シンプルな言葉だと、”背の高さ”などが分かりやすいかもしれませんね。地面からまっすぐだというイメージもあるので、垂直の概念が入りやすいかもしれません。

深澤:それはいいですね。子どもは身体測定で背の高さを測っているでしょうから、その経験に結び付けてあげると具体的にイメージしやすいかもしれませんね。今、垂直の概念とありましたが、垂直の言葉の意味を教えてあげるのも効果的です。”垂”というのは”垂れる”と書いて、雨水などが地面に真っすぐ垂れて落ちる様子を表しているんです。

深澤:この言葉の意味を知っているとわかりやすいのです。神戸市には垂水区という地域がありますが、垂水には”滝”があったとされていますね。垂水の”垂”の字と”滝”の地面に向かって水が落ちる様子をイメージを結びつけると、より垂直の意味が分かりやすいかもしれませんね。
2で割るとは
久保田:垂直の意味が分かっていないだけでなく、垂直の部分、90度の部分に注目しなければならないとわかっているかも大切です。三角形の面積がなぜ2で割るのかをしっかり理解していれば、垂直を見逃すということはないと思うんです。そもそも長方形の面積を計算するときの事を考えてみてください。

宮後:もちろん、4㎝×3㎝で12㎠ですよね。
久保田:これは下の図のように、1㎝×1㎝の正方形がいくつ縦と横に積み重なっているかで考えることができるわけです。

久保田:この考えを理解していると、角度90度の部分が横や縦に隣り合って積み重なっているのがわかります。この段階で垂直の部分が大事であることが見落とさないようになっているんです。さらに三角形の面積の場合はこれに”÷2”が加わるわけですよね。この四角形を縦と横の長さを変えないようにしつつ三角形になるように2つに分けるには、どこで分けるのがよいですか?
宮後:ここで分けるしかないですよね。

久保田:そうですよね。こう見ると、90度つまり、垂直の部分を使って三角形をつくるしかないんですよね。これで90度の部分で縦の長さと横の長さを考えるというの見逃さなくなるんです。
そうすると、まず三角形の面積を考える上で90度の部分を探そうという発想に絶対になるんですよ。そうなると、学力テストの問題で5㎝の部分を底辺として考えると、3㎝の部分や4㎝の部分が高さになるわけがないとすぐわかるはずなんです。
宮後:2で割るを教える時にどう着目させるか、それだけの事なんですがこれで三角形の面積の本質に迫ることができるんですね。これをわかっていると、よくある”2で割るのを忘れる”ということもなくなりそうです。
深澤:このように垂直とはどういうことかを具体的にイメージして理解することと、垂直(90度)の部分を起点として底辺と高さを考える。それを具体的に知ることで、学力テストの問題を間違えることはほぼなくなる正しい理解ができると思います。
子どものの理解を確認する、声掛けの仕方
宮後:要するに、三角形の面積の出し方が【底辺×高さ÷2】だという公式を教えるのではなく、具体的に”底辺・高さ”が何なのか、またその底辺と高さを決めるポイントになる垂直とはどういう考え方なのかを理解してもらうことが大事ということですね。
深澤:端的に言えばその通りです。ですのでお子様に指導する際には、”底辺・高さ”がどの部分なのか、垂直の考えをもとに決めることが出来ているかをよく見てあげるのが、この単元で躓かないポイントだと思います。これは難しいことではありません。
「どこを底辺としたのかな?」
「どこを高さとしたのかな?」
「なぜそこを底辺と高さにしたの?」
これを聞くだけで、三角形の面積に対する誤解は大きく減ります。もちろん形が変わった場合でも理解できているか確認したほうがよいです。ワークには必ずこういう問題もついています。

深澤:このような問題を扱う時も、数字だけに注目していないか子どもの様子をよく見てあげてください。答えがあっているかではなく、”式の意味をきいてみる”のもいいでしょう。7×5÷2と書いていたら、
「7は何かな?」
「5は何かな?」
と聞いてあげるのです。その際に
「なぜ6はダメなの?」
と聞いて、なぜ6㎝の辺が底辺や高さに使えないのかよく聞いてみるのも効果的です。
宮後:これは簡単ですね。今すぐにでも子どもがちゃんと三角形の面積の出し方を理解しているか確認できますね。
久保田:つい私たちも答えや結論だけきいてしまうものですが、小学校5年生はこのようにやり方・考え方の過程の部分に着目することが大切です。前回の円周の際にも同じような話をしましたが、子どもに計算式の意味を問いかけてみるというのは本当に効果的だと思います。宿題をやっていて、答えを間違ったときはつらいものですし投げ出したくなるものです。そんな時に、考え方が間違っているのか、計算間違いしたのかその原因が分かるだけで、もう一度やってみようという気持ちになるのです。原因がわからないのにもう一度やるのは辛いだけです。子どもが算数を嫌がってお困りの方も多いと思います。間違っている理由を計算間違いなのか、考え方の違いなのかはっきりするだけでも取り組みが変わってくる場合がありますね。
宮後:今回は沢山のポイントを伺いました。垂直のイメージの持たせ方から、計算式の意味を伝えることで子どもが理解できているかを確認するというのは、本当に参考になりました。
深澤:今回は、学力テストのお話から引用致しました。特に業界で大きな話題になったのは三角形の面積についてだったのでまずはそのお話をしましたが、学力テストをよく見ると子どもが躓きやすいという問題は他にもまだまだたくさんあります。次回以降もご紹介しながら、子どもや保護者の皆様のためになるお話をしていきたいと思います。次回は子どもたちが良く詰まる”速さ”の問題でお話したいと思います。
まとめ
・垂直はそのままだと理解しにくい。具体的にどういうものかのイメージを
・三角形の面積の高さ・底辺の起点は垂直部分 そこの理解が出来ているかの確認を
・式の意味の問いかけが効果的。問いかけ例を参考に確認してみよう。
