構造力学メモ(その5) 八面せん断応力とミーゼス応力
主応力や、合成応力などとの関連から、ミーゼス応力について慣れ親しんできたと思うが、いまいち、ミーゼス応力とは何なのか、まだイメージしづらいかもしれない。
そこで、八面せん断応力というものを考えて、その量とミーゼス応力の関連が深いことを見ていこう。
1.主応力の方向で考える
まず、ある応力状態について、これまでやったように主応力とその方向(主方向)を求めたあとを考える。主応力は、以前紹介したように、偏差応力の第二不変量と第三不変量、平均応力から求めることができる。主応力が分かれば、3つの主応力ごとに固有ベクトルを求めれば、それが主方向となる。
主方向を、あらためて$${x,y,z}$$軸とすれば、応力テンソルは、対角成分以外$${0}$$の扱いやすい形になる。
すこし注意が必要なのが、応力テンソルは通常は、場所によって値が異なる=主応力、主方向が異なる、以降の話は、局所的に主応力、主方向を考えた場合の話である。
$$
T=\begin{bmatrix}
\sigma_1 & 0 & 0\\
0 & \sigma_2 & 0 \\
0 & 0 & \sigma_3
\end{bmatrix}
$$
2.主方向の(1,0,0),(0,1,0),(0,0,1)でできる正三角形の面を考える。
このとき、$${(1,0,0),(0,1,0),(0,0,1)}$$でできる正三角形の面での応力を考える。この正三角形の面は、面と垂直な法線ベクトルによって表すことができる。例えば、$${\bm{n}}$$に垂直で、点$${\bm{a}=(a_1,a_2,a_3)}$$を通る平面は、$${\bm{n}\cdot(\bm{x}-\bm{a})=0}$$で表される。
この正三角形の面に作用している応力ベクトル$${\bm{t_n}}$$は図.1 のように、テンソル$${T}$$と面を表す法線ベクトル$${\bm{n}}$$の積で表される(このあたりの話は、たいていの教科書に載っているので省略する)。

この面に作用している応力ベクトルを、面に垂直な成分(垂直応力)と、面に平行な成分(せん断応力)に分けるには、図.1 のようにすれば求めることができる。
面に垂直な成分は応力ベクトルと単位法線ベクトルとの内積に法線ベクトルを掛ければ求めることができ、面に平行な成分は応力ベクトルから垂直成分のベクトルを引けば求めることができる。
そして、この正三角形の単位法線ベクトルは、$${(1,1,1)}$$を規格化した、$${(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}})}$$となる。これは、例えば、$${\overrightarrow{AB}\times\overrightarrow{AC}=(-1,1,0)\times(-1,0,1)=(1,1,1)}$$となることからも分かる。
正三角形の面に平行な成分、すなわちせん断応力ベクトルは、図.2 のように求めることができ、偏差応力によって表される。

このせん断応力ベクトルも垂直な二方向に分解できるが、特に意味はないので、それはしない。
(よく見る応力テンソルの説明として、せん断応力を二方向に分けているが、必ずしも、二方向に分けないといけないわけではない。うまく座標軸と面を選べば、垂直応力と一方向だけのせん断応力にすることも当然可能だ。)
そして、このせん断応力ベクトルの大きさを求めると以下のように、その大きさは偏差応力の第二不変量$${J_2}$$で表すことができる。
$$
\tau_n^2=\dfrac{1}{3}\left\{(\sigma_1-\sigma_m)^2+(\sigma_2-\sigma_m)^2+(\sigma_3-\sigma_m)^2\right\}=\dfrac{2}{3}\cdot\dfrac{1}{2}(s_1^2+s_2^2+s_3^2)
$$
$$
\tau_n^2=\dfrac{2}{3}J_2
$$
そして、前回、式変形したように、偏差応力の第二不変量は以下のようにも表すことができる。
$$
\tau_n^2=\dfrac{1}{9}\left\{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2\right\}=\dfrac{2}{3}J_2
$$
3.その他の面も考える
以上の話は、法線ベクトル$${\bm{n}=(1/\sqrt{3},1/\sqrt{3},1/\sqrt{3})}$$で考えていたが、$${+,-}$$を入れても、大きさは2乗和なのでせん断応力ベクトルの大きさは変わらない。
というわけで、以下の8つの単位法線ベクトルに垂直な面で、せん断応力ベクトルの大きさが$${\sqrt{2J_2/3}}$$となる。この8つの法線ベクトルに垂直な面は、正八面体を構成する。
$$
\bm{n_1}=\left(+\frac{1}{\sqrt{3}},+\frac{1}{\sqrt{3}},+\frac{1}{\sqrt{3}}\right)\\
\bm{n_2}=\left(-\frac{1}{\sqrt{3}},+\frac{1}{\sqrt{3}},+\frac{1}{\sqrt{3}}\right)\\
\bm{n_3}=\left(+\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},+\frac{1}{\sqrt{3}}\right)\\
\bm{n_4}=\left(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},+\frac{1}{\sqrt{3}}\right)\\
\bm{n_5}=\left(+\frac{1}{\sqrt{3}},+\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)\\
\bm{n_6}=\left(-\frac{1}{\sqrt{3}},+\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)\\
\bm{n_7}=\left(+\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)\\
\bm{n_8}=\left(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)
$$
なので、$${\tau_{oct}=\sqrt{2J_2/3}}$$を八面せん断応力と呼ぶ。主方向の座標軸の原点を包むような正八面体上に作用する(している)せん断応力ベクトルの大きさを八面せん断応力と呼ぶ、ともいえる。
八面せん断応力と、ミーゼス応力の関係は以下のようになる。
$$
\sigma_{eq}=\sqrt{3J_2}=\dfrac{3}{\sqrt{2}}\tau_{oct}
$$
ミーゼスの降伏条件とは、八面せん断応力、すなわち、主方向の座標軸の原点を包むような正八面体上に作用するせん断応力ベクトルがある値を超えると破壊(降伏)する、という条件であると解釈することができる。
(ミーゼスの降伏条件については、もうひとつ「せん断ひずみエネルギー説」というものもあるので、それもそのうち記事にしたいと思うが、そちらの話は、教科書やインターネット上に結構あふれているので記事にしないかもしれない)。
4.謎の角度 rode角の意味を考える
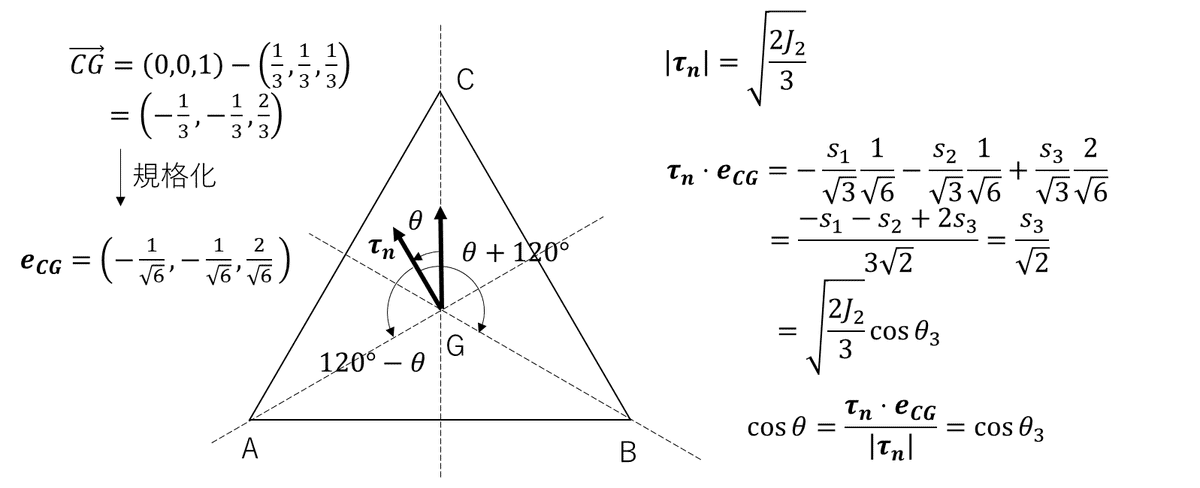
さらに、この正三角形の面に平行なせん断応力の方向も気になるところである。これは、図.3 のように、例えば、Cと正三角形の重心Gでできる直線CGとのなす角度を$${\theta }$$とすれば、その$${\cos\theta}$$は、2つのベクトルの内積を、2つのベクトルの大きさで割れば求めることができる。

そして、図.3 に示すように、偏差応力テンソルの固有値$${s_3}$$は、偏差応力の第二不変量$${J_2}$$と第三不変量$${J_3}$$と、以下の式で求めることができる謎の角度$${\theta_3}$$で表すことができる、結局$${\theta=\theta_3}$$となることが分かる。
$$
\cos3\theta_3=\dfrac{3\sqrt{3}J_3}{2\sqrt{(J_2)^3}}
$$
ただし、$${\theta_3}$$については、今回$${s_3}$$を最小の主(偏差)応力としたわけではないので、$${\theta_3=\theta,\theta-120\degree,\theta+120\degree (0\le\theta\le60\degree)}$$のどれかで、
$${s_3}$$が最大主応力のときは、$${\theta_3=\theta}$$
$${s_3}$$が中間主応力のときは、$${\theta_3=120\degree-\theta}$$
$${s_3}$$が最小主応力のときは、$${\theta_3=\theta+120\degree}$$
($${\cos(\theta-120\degree)=\cos(120\degree-\theta)}$$なので、$${\theta-120\degree}$$と$${120\degree-\theta}$$の違いは、あまりない)。
$$
\cos3\theta=\dfrac{3\sqrt{3}J_3}{2\sqrt{(J_2)^3}}
$$
この$${\theta}$$のことをrode角と呼ぶ。またはローデ角、ロード角と呼ぶ。rode角については、正八面体の面上のせん断応力ベクトルの方向を表す量と解釈することができる。そして、正八面体の面上のせん断応力ベクトルは、図.4 に示すように、$${0\le\theta\le60\degree}$$の方を向いている、すなわち、最大主応力方向から$${\theta}$$ずれている、と言える。
rode角$${\theta}$$は、単なる方向だけを表していることから、せん断応力ベクトルの大きさには影響せず、ミーゼスの降伏条件がなぜ、第二不変量$${J_2}$$のみで表現できたかも理解できるのではないだろうか。($${J_3}$$は、$${\theta}$$で表すことができるので、$${\theta}$$に依存しない$${=J_3}$$に依存しない、と言える)。
5.おわりに
今回は、八面せん断応力を考えてみて、それと主応力や偏差応力の第二不変量やミーゼス応力、そして、主応力を計算したときに出てきた謎の角度rode角との関連について触れてみた。
全く意味の分からなかったミーゼス応力がだいぶイメージしやすくなったのではないだろうか。
今後は、八面せん断応力だけでなく色々な面のせん断応力ベクトルの大きさや、せん断ひずみエネルギーについて記事にしてみたいと思う。
この記事が気に入ったらサポートをしてみませんか?
