構造力学メモ（その４）　高校数学と偏差応力の第二不変量とミーゼス応力

　今回の話題は、構造力学とはあまり関係ない。
　偏差応力の第二不変量の式から、よく見かける形式に変形する際に1度すべて展開して頑張って計算していたが、もう少し楽に式変形してみる。
　3変数の展開式をふんだんに使うので、高校数学の式変形の演習として良さそうではある。

１．偏差応力の第二不変量

偏差応力の第二不変量は、以前紹介したとおりである。

偏差応力の第二不変量$${J_2}$$は、以下のように計算される。

$$
 J_2 =\dfrac{1}{2}\sum_i\sum_js_{ij}s_{ij} =\dfrac{1}{2}(s_{11}^2+s_{22}^2+s_{33}^2+2s_{12}^2+2s_{23}^2+2s_{31}^2)\\
$$

それが、以下の式に等しい。これは教科書ではあまり導出せず、突然この数式を出してくるので、はじめてみたときは少し驚いてしまう。

$$
 J_2 =\dfrac{1}{6}\{(\sigma_x-\sigma_y)^2+(\sigma_y-\sigma_z)^2+(\sigma_z-\sigma_x)^2+3\tau_{xy}^2+3\tau_{yx}^2+3\tau_{zx}^2\}
$$

前回は頑張って計算したら、高校数学によく出てくる形式となったので、それを式変形したが、もう少し楽に式変形してみよう。

２．もう少し楽な式変形

　偏差応力テンソルは以下のようになる。

$$
\begin{bmatrix}
s_{11} & s_{12} &s_{13} \\
 & s_{22} &s_{23} \\
sym &  &s_{33}
\end{bmatrix}
=\begin{bmatrix}
\sigma_{x}-\sigma_m & \tau_{xy} &\tau_{xz} \\
 & \sigma_{y}-\sigma_m &\tau_{yz} \\
sym &  &\sigma_{z}-\sigma_m
\end{bmatrix}
$$

$$
\sigma_m=\dfrac{\sigma_x+\sigma_y+\sigma_z}{3}
$$

なので、それを最初の偏差応力の第二不変量の式に代入すると以下のようになる。

$$
 J_2 =\dfrac{1}{2}\{(\sigma_x-\sigma_m)^2+(\sigma_y-\sigma_m)^2+(\sigma_z-\sigma_m)^2+2\tau_{xy}^2+2\tau_{yx}^2+2\tau_{zx}^2\}\\
$$

ここで、$${\sigma_m=(\sigma_x+\sigma_y+\sigma_z)/3}$$を代入するが、それぞれを以下のように変形して$${X,Y,Z}$$とおく。

$$
\sigma_x-\sigma_m=\dfrac{2\sigma_x-\sigma_y-\sigma_z}{3}=\dfrac{1}{3}\left\{(\sigma_x-\sigma_y)-(\sigma_z-\sigma_x)\right\}=\dfrac{1}{3}(X-Z)
$$

$$
\sigma_y-\sigma_m=\dfrac{2\sigma_y-\sigma_z-\sigma_x}{3}=\dfrac{1}{3}\left\{(\sigma_y-\sigma_z)-(\sigma_x-\sigma_y)\right\}=\dfrac{1}{3}(Y-X)
$$

$$
\sigma_z-\sigma_m=\dfrac{2\sigma_z-\sigma_x-\sigma_y}{3}=\dfrac{1}{3}\left\{(\sigma_z-\sigma_x)-(\sigma_y-\sigma_z)\right\}=\dfrac{1}{3}(Z-Y)
$$

このとき、以下のように$${X+Y+Z=0}$$となる。

$$
X+Y+Z=(\sigma_x-\sigma_y)+(\sigma_y-\sigma_z)+(\sigma_z-\sigma_x)=0
$$

$${X,Y,Z}$$を$${J_2}$$に代入して、展開すると以下のようになる。

$$
 J_2 =\dfrac{1}{2}\cdot\dfrac{1}{9}\{(X-Y)^2+(Y-Z)^2+(Z-Y)^2+\cdots \}
$$

$$
 J_2 =\dfrac{1}{2}\cdot\dfrac{1}{9}\{X^2-2XY+Y^2+Y^2-2YZ+Z^2+Z^2-2ZX+X^2+\cdots \}
$$

$${XY+YZ+ZX}$$を求めたいが、これまた高校数学でよく出てくる$${X+Y+Z,XY+YZ+ZX}$$から、$${X^2+Y^2+Z^2}$$を求めるような問題の常套手段である、$${(X+Y+Z)^2}$$を求めてみる。

$$
 (X+Y+Z)^2 =X^2+Y^2+Z^2+2XY+2YZ+2ZX
$$

そうすると、以下のように$${XY+YZ+ZX}$$を$${X^2+Y^2+Z^2}$$で表すことができる。

$$
-2XY-2YZ-2ZX =X^2+Y^2+Z^2
$$

これを$${J_2}$$に代入すれば、求める式を得ることができる。

$$
 J_2 =\dfrac{1}{2}\cdot\dfrac{1}{9}\{3X^2+3Y^2+3Z^2+\cdots \}
$$

$$
 J_2 =\dfrac{1}{6}\{X^2+Y^2+Z^2+\cdots \}
$$

３．おわりに

　以前紹介したものよりは、多少楽に偏差応力の第二不変量$${J_2}$$を、元の応力テンソルから求めることができた。
　高校数学の受験数学でよく出てくる、3変数の展開や対称式が出てくるので、高校数学の式展開の問題として、何気なく以下のように出題してみてもいいかもしれない。

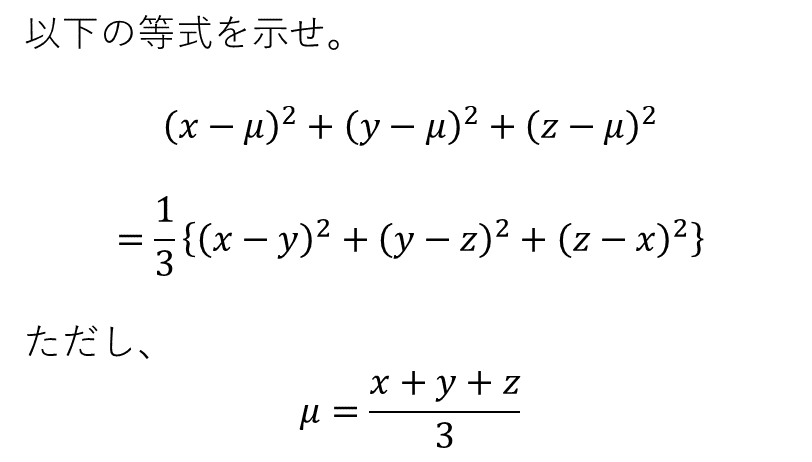
　結構面倒な計算をして、「こんな計算に何の意味があるんだ？」と苦痛を与えたところに、「この式は、ミーゼス応力という橋の設計にも使われるような値の計算の一部なんだよ。」と言ってみると面白いかもしれない。

その５