
3-3.いまさらきけない方程式(等式の性質とその使い方)
等式の性質は、「そんなの当たり前じゃん」というくらい自然なものです。それをいちいち議論しておくのは、論理(※1)を重んじるからです。「昨日は機嫌がよかったから許したけど、今日は虫の居所が悪いからダメだ」とか「支配者が変わったから、この定理は受け入れられない」とか「昔とは世の中が違うからこの定義は許されない」ということのないようにです。誰もが論理的に考えたら同じ結果がもたらされるというのは大事なことですね。
等式の性質は、「同一と見なしているのなら、同じ操作を施した結果も同一のものになる」というものです。「同一とみなしている」を表しているのが「等号」です。では具体的にその性質を並べます:a=b(aとbが等しい)なら、次の①~④が成り立ち、かつ、その逆も成り立つ。ただし、c≠0。
①同じ数を足しても等しい:a+c=b+c
②同じ数を引いても等しい:a-c=b-c
③同じ数を掛けても等しい:ac=bc
④同じ数で割っても等しい:a/c=b/c(ただし、c≠0 ※2)
軽く説明しましたが、当時中学生の私は何を言っているのか理解できませんでした。それは、a=bを5=5のように解釈していたからです。このように理解していると、「あたり前田のクラッカー」いや「あたり前のこんこんちき」なのです。
ここでは次のように解釈するのがいいのです。3・2+4=10 を利用して、
aの部分が3・2+4で、bの部分が10 と考えるのです。もちろん、他の数でもいいです。式が単純でない方がいいです。次に、cを5としましょう。等式の性質が成り立っているか、各自確かめてみてください。(※3)
今後、代数方程式と言わずに、単に方程式と呼ぶことにします。
1次方程式を解けるようになるのが目標です。次の2つの形が解けるようになれば、1次方程式の解法はほぼ終りです:(1) x+7=3 (2) -3x=6
「方程式を解く」というのは、与えられた方程式を満たす未知数の正体を明らかにすることです。答えの形は、「x=△」の形で表されます。いまは、1次方程式を解くので、正体はただ一つです(代数学の基本定理)。
(1)の式は、未知数xが左辺にしかないので、左辺の+7がいなくなれば左辺はxだけとなります。そこで、②の性質を使って、両辺(左辺とと右辺)から7を引けばうまくいきます。
注意すべきことは、等号が成り立ったまま式を変形することです。だから、等式の性質をうまく使うのです。
(1)の式は、(x+7)-7=3-7 ⇒ x=-4.
または、①の性質を使って、両辺に-7を足してもうまくいきます。
すると、①の式は、(x+7)+(-7)=3+(-7) ⇒ x=-4.
※マイナスの話や多項式の話でしたように、どちらも本質的には同じです。
(2)の式も、未知数が左辺にしかないので、xにくっついている-3が消えればいいですね。ところで、左辺は (-3)・x ということだから、-3が1に変えられればいいのです。そのためには、2つの方法があります。でも本質的には同じことをします。④の性質を使って、両辺をー3で割れば1になるのでうまくいきます。もしくは、③の性質を使って、両辺に-1/3を掛けてもうまくいきますね。
④の性質を使った場合は、(-3x)/(-3)=6/(-3) ⇒ x=-2.
③の性質を使った場合は、-3x・(-1/3)=6・(-1/3) ⇒ x=-2.
※記号「⇒」は「左から右に変形できます」という記号です。
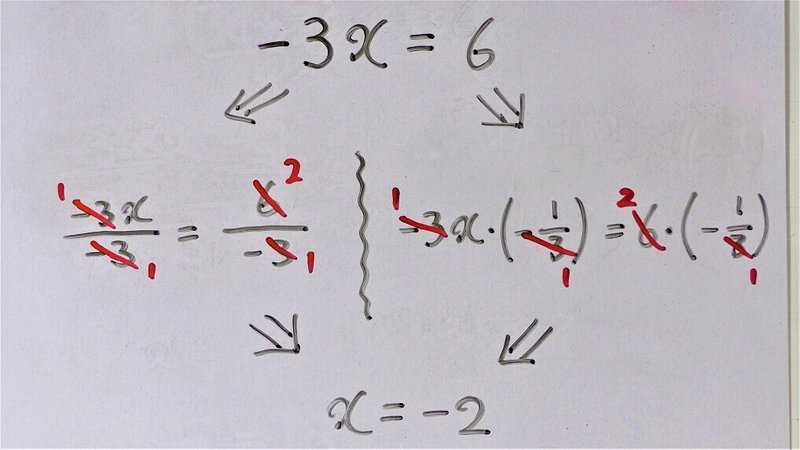
好みで選んでください。
さて問題です。①の根は-4、②の根は-2と求めましたが、それらが正しいという理由を答えられますか。これに答えられて、はじめて方程式が解けたといえます。答えは最後にあります。(※4)
詳しくは次回書きますが、1次方程式は ax+b=0 の形(a, b はある数)が基本なので、もうすべてを解くことができます。▢(←終りの記号です)
解説動画←クリックすれば見られます
※1 考えや議論が筋道に沿って展開されること。残念ながら、一般の会話などでは「論理」と「理論」がごちゃ混ぜに使われています。一方で「ロジック(logic 論理的)」は、正しく使われているようです。
尚、「理論」は、論理によって組み立てられた知識の集合体。ガロア理論、相対性理論など。
※2 c≠0は「cは0ではありません」を表現している記号です。中学数学をやっているだけだと、このことの大切さには気づきません。文字式で割る話も割りたくなるのも、高校数学からです。ただ、この数学事始めでは、いつになるかまだ決めていません。尚、「0で割る話」は動画にも記事にもしてあります。クリックすればそこに飛びます。
※3 ①から確かめます:(3・2+4)に5を足すと15ですね。他方、10に5を足すと15です。左辺と右辺の結果が一致しました。
次は②を確かめます:(3・2+4)から5を引くと、5です。他方、10から5を引くと、やはり5です。左辺と右辺の結果が一致しました。
次は③を確かめます:(3・2+4)に5を掛けると50です。10に5を掛けると50です。やはり、左辺の計算結果と右辺の計算結果が一致しました。
最後は④です:(3・2+4)を5で割ると2です。もう一方の10を5で割るとやはり2です。これも結果が一致しました。
具体的ですが、確かに①~④が成り立つことは確認できました。ここで終わってはいけません。最初の主張は、逆も成り立つといっているのですから、逆も確かめます。つまり、①だと (3・2+4)+5 と 10+5をそれぞれ確かめましたから、5を足す前が一致しているかどうかを見ます。さてどうですか。当然、一致しています。②は (3・2+4)-5 と 10-5で、5を引く前を見ますが一致していますね。同様に、③、④を確かめますが当然一致しています。これで確認ができました。
※数学で、pだったらq、その逆のqだったらpということを確かめるとき、多くの場合、どちらか一方は証明しやすいものです。数学していると、そういうことが多々あります。
※4 この段階できちんと答えられたら、私よりもかなり数学ができます。
理由は、-4を(1)のxに当てはめたとき、等号が成り立つからです。実際、
左辺=(-4)+7=3で、これは右辺の3と一致します。
同様にして-2を(2)のxに当てはめると、左辺=-3・(-2)=6 となり、右辺の6と一致します。
このことは3-1.で説明しましたが、大抵は忘れてしまいます。いろいろと覚えることがあるから当然だし、人間なら必然です。
私は、新しいことを学んでも直ぐに忘れてしまうので、現在は、どうしても覚えたいものは紙片に書いてトイレにクリップで吊り下げています。
人は忘れるから日々平穏に過ごせるのです。もしも忘れなかったら大変です。良いことだけでなく、嫌なことも悪いことも忘れたいことも、ず~~っと覚えているのです。それも明確に。たまったものではありません。
この記事が気に入ったらサポートをしてみませんか?
