どうでもいいけどパース2

さて、前回どうでもいいパースについて書いてみました。これですね。

それで、上のような図を描いていると、もう一つ気になることが出てくるのです。どうでもいいついでにもう少し書いてみます。

それはなにかというと、

これは車両を真横から見た図ですが、この均等に並んでいる窓ですね。

つまりこれらの窓が遠近法的空間ではどのように描かれるべきなのか。どうやって均等に並んでいる位置を正確に見つければいいのかという問題です。

そんなの、こんなふうにテキトーに描けばいいんじゃないの？

そう、絵なんだしテキトーでいいと僕も思います。電車の窓が並んでいるんだなということはじゅうぶん伝わりますし。なので、実際に絵を描くときは全然気にする必要ないのです。ただ、それを言った上で、もし遠近法的に位置を知るにはどうしたらいいのかというのを説明してみようと思います。

まず、真横から見た図で考えてみます。

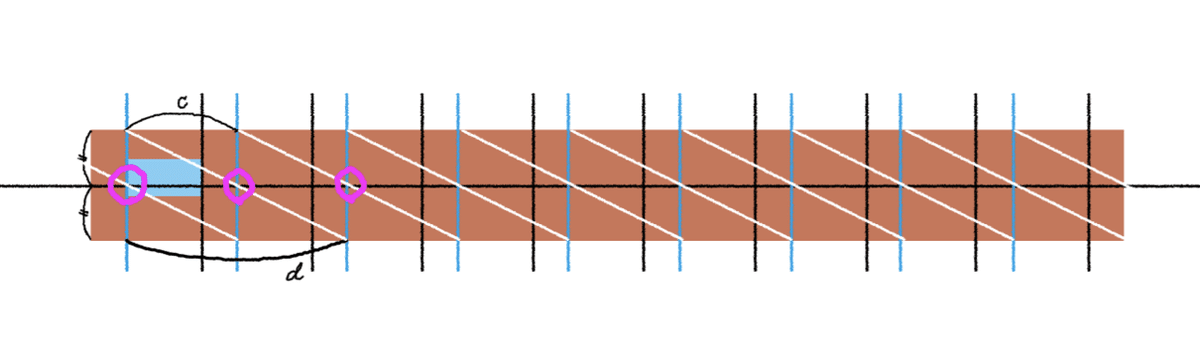
最初の一個目の窓はだいたいこのくらいの大きさかな、と描いてみて、次に上端と下端から等距離になる位置に中心線を描きます。

一つ目の窓の右端の位置までをaとすると、2つ目の窓の右端の位置bが知りたいわけです。

左上の角からピンク色の丸で囲んだ部分を通る直線を引き（白い線）、これが下端の線と交差する部分が位置bになります。白い線はつまり、長辺をbとする長方形の対角線を引いたことになり、対角線が中心線と交差する部分はその長方形の中心（ピンクの丸）です。

これを連続させると、上の図のように次の窓の右端の位置が得られます。

次に窓の左端の位置ですが、

このように真横から見た図では、対角線を平行に同じ分だけずらせば位置が得られますが…

遠近法空間でやってみます。

VPに収束する中心線を引き、左上の角からピンク色の丸で囲んだ部分を通る直線を（白い線）を引くと、次の窓の右端の位置が得られます。

あとは繰り返せばいいだけです。

次に窓と窓の間隔e（青い線）ですが、これに関しては前回と同じ考え方で、ELの適当な位置にRPを取り、そこからe'を求めます。

e'の左端から中心線と窓の右端の交差点（ピンクの丸）を通る線を延ばしていき、もう一つのRPを見つけます。

e'の右端からRPを結び、中心線と交差したところが次の窓の始まる位置です。ここまでくればあとは次々と対角線を引いていけばいいということになります。

もっと簡単な方法もあります。

aの長方形の対角線を引いていきます。

窓の左端（青い線）と対角線が交差する点（ピンクの丸）を見つけます。

ピンクの丸の点とVPを結ぶ線を引きます。その線がそれぞれ対角線と交差する点が窓の左端の位置になります。

それぞれの対角線は３次元空間では平行であることを考えると、遠近法空間では対角線を延長していけば一点に収束するはずなので、他にもやり方があると思います。

これはビルの窓を描いたりするのにも使えますね。また、均等に並んでいないものを遠近法空間に正確に配置するときもやり方があります。

遠近法の使い方について少し書いてきましたが、とりあえずこの辺で終わりにしておきます。絵を描くにあたって、遠近法の習得は個人的にはそんなに大事なことであるとは考えませんが、リクエストがあればいくらでも書けそうなテーマではあります。