関学声研ブログ 第23回

　どうも熱です。2回目の投稿となりました。今回も数学と絡ませてお話していきたいと思います。

　第2回のテーマは「ガチャと確率」です。現在、数多くのソーシャルゲーム(以下ソシャゲ)が多くリリースされ、そこに「ガチャ」は不可欠な存在となりました。目当てのカードを手に入れるために数年間貯めていた貯金を崩し、ウン万円スった友人が僕にはいますが、ガチャというものは時に人を狂わせると僕は勝手に思ってます。

　各ソシャゲにおいて「排出率」なるものが設定されています。最高レアリティはこんな確率で出るよ、みたいな数値ですね。知ってる範囲では大体3%ぐらいでしょうか。高めの5%だったり強気の姿勢な0.3%に設定してるところもありますね。(たまに「最高レアリティ排出率10倍！」みたいなガチャ用意してくるんですがユーザーは皆「でもどうせ3%じゃん」と口を揃えて言います)

　さて、今回は以下のテーマについて議論したいと思います。

何回ガチャを回せば最高レアリティを引くことができるか？

　「最高レアリティ(以下SSR)が欲しい！」と思ったとき、果たして何回回せば1枚は手に入るかを気になったことは一度はあるはずです。(無いわ！という方はすみません)　具体的に計算していきたいと思います。

　方法としては、幾何分布というものを考えます。定義としては以下の通りです。

　Bernoulli試行を繰り返して、初めて成功するまでに失敗した回数Y=X-1の分布。

　ここで、Bernoulli試行というのは「コイントスをして表か裏が出る」といった2択しか結果がないような事象のことです。つまり、幾何分布というのは、欲しい結果が出るまでに失敗した回数のことを指します。ガチャの話に当てはめると「SSRを出すまでに引いたガチャの回数」です。よって、SSRが出る確率をpとすると、n回目に初めてSSRを引く確率は次の式で表せます。

　それではこれを用いて具体的にpを決定して議論していきたいと思います。

　pの値を3%と5%に設定し、n回目(1≦n≦100)に初めてSSRを引く確率をグラフにしてみました。赤色が3%、青色が5%のグラフです。

　3％においては、40回を超えるとやっと7割を超えてきます。5%においては24回目において7割を超えていきます。グラフを見れば分かりますが、回数を増すごとに段々と値は100%に近づいていきます。（nを∞に弾き飛ばせば1に近づきます）このことから、次のことが言えます。

出るまで回せばいつか出る

　ガチャを課金して回すときは財産を失わないように気を付けてくださいね。無理は禁物ですよ。

　また、この幾何分布において期待値が以下の通り定義されています。

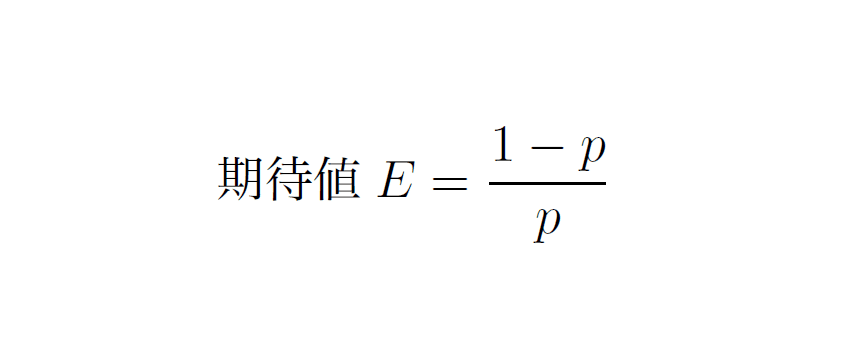
　その前に、期待値の話をしておきましょう。実は高校数学の数学Bの教科書に載っています。ただ、本によっては平均と表記する場合もあるようですが、同じ意味です。「え？そんなのやったっけ？」って方はセンター試験を思い返してみてください。(受けてないって方はごめんなさい)前半2問が数学Ⅱの問題で後半2問数列からベクトルの問題を解いたと思いますが、第5問もありましたよね？　それが数学Bの3つ目の単元「確率分布」です。大体の高校生がすっ飛ばしてる内容です。この単元において詳しくやるようです。(僕は大学2回生で学びました)

注) どうやら今度の指導要領改訂において数学Bからベクトルが数学C送りされるようです。その影響で学校で確率分布の単元を扱うようになるかもしれません。

　さて、余談が長引きましたが、期待値が持つ意味としては「確率を考慮した平均」です。ざっくり言うと「大体平均としてこんぐらいの値になるよ」という指標の数字です。それでは上の定義式に基づいて、先程の例の3%と5%の場合において期待値を計算してみましょう。

　よって、上の計算により3%において約32連目、5％において19連目においてSSRを引いてくると大体平均になっていることが分かります。なので、これを下回る回数で引けたなら人並より運が良いですし、この回数を上回っても出ない場合も十二分にあり得る話となります。怖いですね。

　これらの話はあくまで理論上の話です。鵜呑みにはしないでください。やはり、

出るときは出る、出ないときは出ない。

というもののがガチャというものだと思います。

熱