
本当は面白い物理の授業 008 水平投射
今回の授業は、「水平投射」です。
高校物理の「水平投射」の問題は、「空気抵抗を考慮しない」ことが前提条件です。
前回の授業でも記載しましたが、「空気抵抗」を考慮すると、極端に計算が難しくなるからです。
それでは、「水平投射」について考えていきましょう。
「水平投射」とは、「物体を水平方向に投げ出す」ということです。
「距離の長いキャッチボール(50m程度)」を想像してください。
ボールを「投げる人」は「受ける人」を目掛けてボールを投げます。
通常、ボールを「投げる人」は、「ボールが重力で落下する」ことを考慮し、斜め上に投げ出します。
これは、「水平投射」ではありません。(下図)
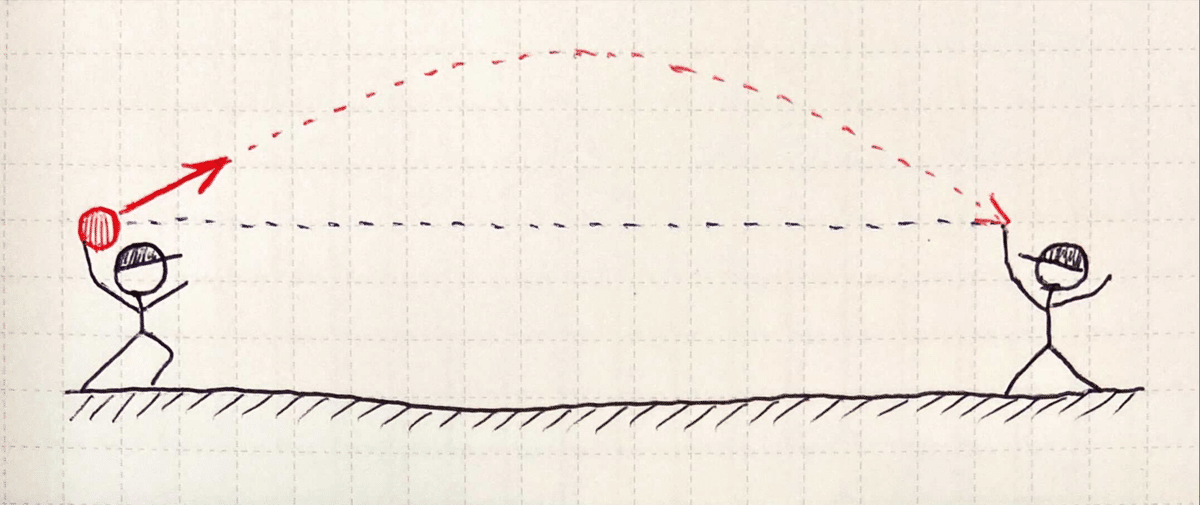
「水平投射」とは、「水平な方向(地面と並行)」にボールを「投げ出す」ことです。(下図)

もし、地球の「重力」が無ければ、ボールは地面と水平に進みます。
そして、「空気抵抗」がなければ、ボールの速度は一定のまま、どこまでも飛んでいきます。
何故なら、「ボールの速度を減速させる力」が何も働いていないからです。
しかし、実際には「空気」も「重力」も存在します。
「空気抵抗」により、ボールは減速し、
「重力」により、地面に向かって落ちていきます。
ただし、
高校物理での「水平投射」では、
「重力」を考慮しますが、
「空気(空気抵抗)」を考慮しません。
これが意味することは、
ボールが・・・
「水平方向」には、「等速度運動(常に一定速度で動く)」し、「鉛直方向(上下方向)」には、「自由落下」の運動をする (下図)

ということです。
ボールの動きが想像できるでしょうか?
この様な現象を想像する時、
とっておきの方法があります。
それは、
「自分自身が、そのものになった」
と考えることです。
ここでは、「自分自身がボールになった」と考えます。
想像してください・・・
建物の屋上にスケートリンクがあります。
滑らかな氷の上をスケート⛸で滑っています。
風は自分が進む方向に同じ速度で吹いています。
風の抵抗はありません。
そして、そのまま建物の屋上から飛び出します。
飛び出した瞬間に、重力に引っ張られて下方向にも落ちていきます。風の抵抗はないので、水平方向の速度は一定です。
下方向には、加速していきます。
(危険⚠️なので、こんなことはできませが)
ボールの「水平投射」は、この様なイメージです。
当然、投げられたボールは一つです。
よって、「水平方向」と「鉛直方向」とで別々の動きをするわけではありません。
「水平方向」と「鉛直方向」の二つ運動が合成された動きをします。
ここで、これまで勉強してきた「ベクトル(の合成)」の登場です。
「水平方向」の速度をX軸方向のベクトルと考え、
「水平方向の速度」を「Vx」
「水平方向の移動量」を「Y」
「鉛直方向」の速度をY軸方向のベクトルと考え、
「鉛直方向の速度」を「Vy」
「鉛直方向の移動量」を「Y」

とおきます。
まずは、「水平方向の速度」だけを考えてみましょう。
「水平にボールを投げ出した瞬間のボールの速度」を「Vo」とした時、水平方向のベクトルは、ずっと「Vo」のままです。
そして、X軸方向への移動量は、速度が一定であるため、「初速 Vo」に「時間 t」をかけたものになります。
Vx = Vo
X = Vo ✖️ t
下図は「水平方向」の速度だけを取り出した図です。

次に、「鉛直方向の速度」を考えましょう。
「鉛直方向」は「自由落下」です。
ボールが手から離れた瞬間の速度は「0」ですが、「重力」によって、どんどん加速していきます。
よって、重力加速度を「g」とすると、
Vy = g ✖️ t
Y = 1/2 ✖️ g ✖️ t ^ 2
下図は、「鉛直方向」の速度だけを取り出した図です。

「自由落下」を復習したい方は、「007」の記事を確認してください。
さて、ここからが「速度のベクトルの合成」です。
図に描いてみましょう。
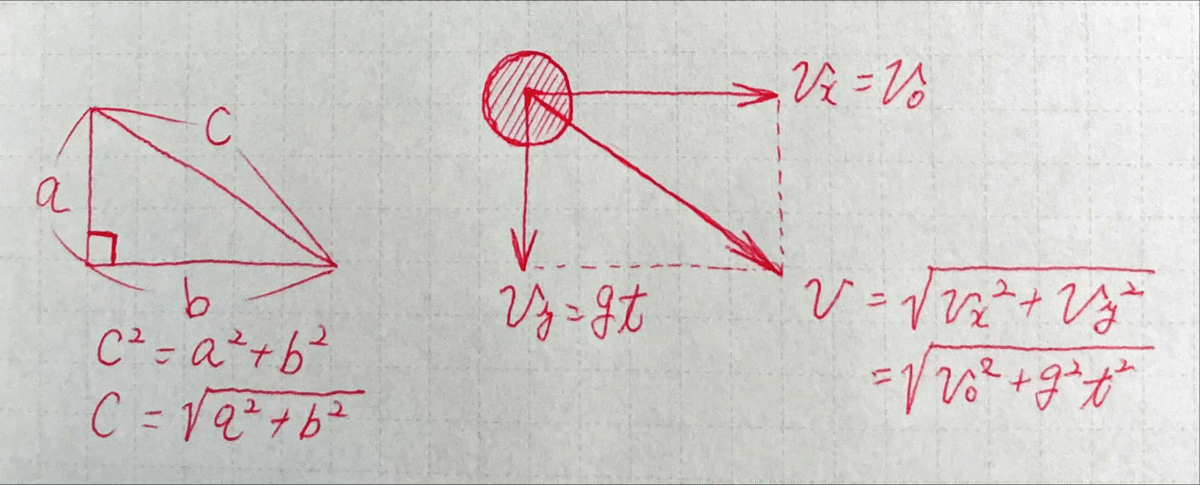
「水平方向」と「鉛直方向(下向き)」を合成すると、「斜め下を向いたベクトル」ができます。
これが、実際にボールが動いている方向です。
初期は、「鉛直方向の速度」は「0」です。
よって、「速度のベクトル」は「水平方向」を向いています。

段々と「鉛直方向の速度」は加速していきましすので、「合成速度のベクトル」は下方向を向いてきます。
「合成速度」を「V」とすると、
V = √(Vx ^ 2 + Vy ^ 2)
次回の授業では、実際に数値を入れて計算し、それを図に描いてみます。
本当は面白い物理の授業009へ続く。
この記事が気に入ったらサポートをしてみませんか?
