【3.14】円周率の日にPythonでπを近似

3月14日。3.14。本日は円周率の日ですね。
そこでnoteを始めて最初に迎えた円周率の日を記念して（？）、円周率に関する記事を書いてみたいと先程思いつきました。

半径1の円に内接する正多角形と外接する正多角形の面積で円周率$${ \pi }$$を近似するPythonプログラムの話を投稿したいと思います。

正六角形による近似

円に内接する正六角形

円に外接する正六角形

正六角形の場合の評価式

半径1の円の面積は$${ \pi }$$ですので、$${ S_1 < \pi < S_2 }$$が成り立ちます。すなわち、上の計算から、

$$
\frac{3\sqrt{3}}{2} < \pi < 2\sqrt{3}
$$

です。ここで、$${ 1.7320 < \sqrt{3} < 1.7321 }$$より、

$$
\frac{3 \cdot 1.7320}{2} < \pi < 2 \cdot 1.7321
$$

が成り立ちますので、$${ 2.5980 < \pi < 3.4623 }$$になります。

これをPythonを使って計算すると、次のようになります。

import math
S_1 = 1/2 * 6 * math.sin(math.radians(60))
S_2 = 6 * math.tan(math.radians(30))
print(S_1,"< π < ", S_2)

実行結果：

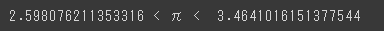
一般化

半径1の円に内接する正$${ n }$$角形の面積を$${ S_1 }$$、外接する正$${ n }$$角形の面積を$${ S_2 }$$とします。

このとき、三角形の面積の公式から$${ S_1,  S_2 }$$はそれぞれ、次のようになります。

$$
S_1 = n \cdot \frac{1}{2} \cdot 1 \cdot 1 \sin \left( \frac{{360}^{\circ}}{n} \right) = \frac{n}{2}\sin \left( \frac{{360}^{\circ}}{n} \right)
$$

$$
S_2 = n \cdot \frac{1}{2} \cdot 1 \cdot 2 \tan \left( \frac{{180}^{\circ}}{n} \right) = n\tan \left( \frac{{180}^{\circ}}{n} \right)
$$

$${ S_1 < \pi < S_2 }$$が成り立ちますので、

$$
\frac{n}{2}\sin \left( \frac{{360}^{\circ}}{n} \right) < \pi < n\tan \left( \frac{{180}^{\circ}}{n} \right)
$$

が成り立ちます。
それでは、Pythonで正72角形(n=72の場合)を計算してみましょう。

n=72
S_1 =  1/2 * n * math.sin(math.radians(360/n))
S_2 = n * math.tan(math.radians(180/n))
print(S_1,"< π < ", S_2)

実行結果：

n=72のときでも、まだ真の値と小数第2位まで一致するような近似ができません。

そこで最後に、$${ S_2 - S_1 < 0.001 }$$になるような最小の自然数$${ n }$$を求めてみましょう。

n=72
while True:
    S_1 =  1/2 * n * math.sin(math.radians(360/n))
    S_2 = n * math.tan(math.radians(180/n))
    if S_2-S_1 < 0.001:
        break
    n = n + 1
print("正",n,"角形のときに、次の不等式が成り立つ。")
print(S_1,"< π < ", S_2)

実行結果：

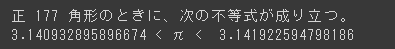
今回はかなり思い付きで記事を書いてしまったため、かなり荒い内容になってしまいました。
来年は、もうちょっと練ってから書いてみます。（多分忘れる。）

とりあえず、本日中に投稿できて良かったです。
最後までお読みいただきありがとうございました！