
物理量の「足し算」や「掛け算」は図式で表すと直観的かも
拙著『図式と操作的確率論による量子論』で紹介している「操作論」は,いたるところで現れます。その簡単な具体例の一つとして,「物理量の足し算」や「物理量の掛け算」について紹介します。この記事は,操作論を知らない読者でも読めるように(ていねいに読めば中学生でもわかるように),わかりやすく書いています。
物理量の足し算
まず,「物理量の足し算」の世界について述べます。「2メートル」という物理量を,次のように表すことにします。

「物理量の足し算を行う」という演算を,次式のように表します。

「$${2\mathrm{m}+3\mathrm{m}=5\mathrm{m}}$$」という式は,次のように表せます。

ここで,「3を足す」という演算を,次式のように定義します。

すると,先ほどの式「$${2\mathrm{m}+3\mathrm{m}=5\mathrm{m}}$$」は次のようにも表せます。

なお,「$${3\mathrm{km}}$$」は次のように表せます。

「$${2\mathrm{m}+1\mathrm{g}}$$」のように異なる物理量の和も表せます。
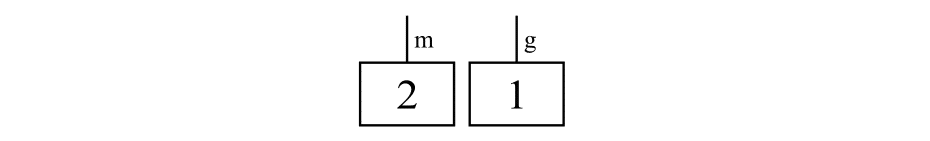
ただし,単位が異なる場合には,通常はまとめられないと考えたほうがよさそうです。同じ単位はまとめることができて,たとえば「$${2\mathrm{m}+1\mathrm{g}+1\mathrm{m}=3\mathrm{m}+1\mathrm{g}}$$」のような計算は次のように表せます。
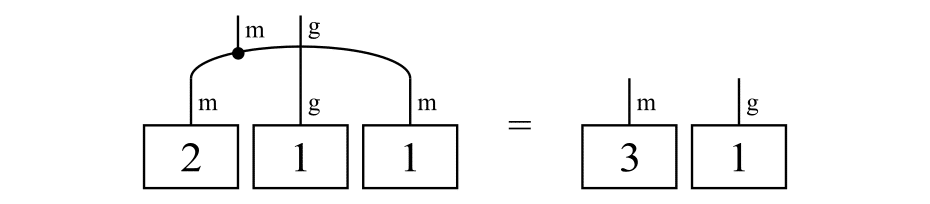
補足:操作論との対応関係を述べておきます。「$${\mathrm{m}}$$」のような単位や「$${\mathrm{m}}$$と$${\mathrm{g}}$$の和」のような単位の和が系であり,無単位が自明な系です。上の図式では自明な系を省略しています。和が並列接続で,「$${+0}$$」が恒等プロセスです。
物理量の掛け算
「足し算の世界」とは別の世界として,「掛け算の世界」も考えることができます。「2メートル」は,次式で表せるのでした。

「2メートルで割る」ことを表す物理量も考えられます。

なお,「足し算の世界」でも同様に,引き算を表す物理量を導入できます。
どのような物理量に対しても,それらの「掛け算を行う」演算が考えられます。

「$${6\mathrm{m}÷2\mathrm{s}=3\mathrm{m/s}}$$」は,次式で表されます。

また,「$${4\mathrm{m}÷2\mathrm{m}=2}$$」は,次式で表されます。

この式は

とも表せます。ただし,

です。
補足:操作論との対応関係を述べておきます。「$${\mathrm{m}}$$」や「$${\mathrm{g \cdot m}}$$」のような単位が系であり,無単位が自明な系です。積が並列接続で,「$${\times1}$$」が恒等プロセスです。
このような「足し算の世界」や「掛け算の世界」を一般化した理論が操作論です。操作論は非常にシンプルな理論でありながら,線形代数や量子論などを始めとするさまざまな理論の基盤となっています。
足し算と掛け算の混在
二つの世界を合わせて「足し算と掛け算の世界」を考えたくなると思います。上で紹介した「足し算の世界」を拡張すると「足し算と掛け算の世界」を比較的素直な形で表現できると思います。詳細は省きますが,たとえば「$${6\mathrm{m}÷2\mathrm{s}-1\mathrm{m/s}}$$」は次のように計算できます。

補足:大ざっぱに述べると,掛け算を直列接続で表して足し算を並列接続で表せば,操作論とみなせます。
さいごに
操作論の図式が活用できる簡単な例として,物理量の四則演算の例を紹介しました。数式に慣れている人にとっては,物理量の四則演算を行う際にこのような図式を用いることのメリットはあまりないような気がします。しかし,数式に慣れていない人にとっては,この図式をイメージするとわかりやすいかもしれません。また,より高度な話として
物理量の四則演算がもっている構造そのものについて考えたい場合
「物理量以外のモノ」の演算に拡張して考えたい場合
などには,このような図式が威力を発揮する場面が少なからずあると思います。
