電気のおはなしその56・交流の性質(8)直列電圧はベクトル和
前回・前々回と使いまわした図ですが、

このように、位相が同じ電圧波形を直列にすると、直列電圧は各々の波形の和になります。100Vと100Vを直列にすると、合計200Vになります。
それに対して、

位相が180°逆の波形を直列にすると、合計電圧はゼロとなりました。
ところで、交流のベクトルとは一体何だったのか、再確認しましょう。
ベクトルとは、円周上を反時計回りに回転する点を、円の中心と円周上の点を結ぶ矢印で表したものでした。ベクトルの矢印の長さを右側から見たとき、それはsin波形の大きさを表していました。
つまり、ベクトルは、その瞬間における電圧などの波形の大きさを表しています。
ということは、電気のおはなしその12で書いたように、ベクトルどうしの足し算は、交流電源を直列に接続したときの電圧の大きさを表すのではないでしょうか。
( ゚Д゚)ノそのとーりです!
そうなんです、ベクトルの矢印をつないで作ったベクトルの合成値は、直列にした二つの交流電圧の値を表しています。また、並列にした二つの交流電流であっても、やはりベクトルの足し算で表すことができます。
では前回・前々回に例示した波形で、具体的なベクトル和を求めてみます。
まず、同相であるVaとVbの直列の場合。
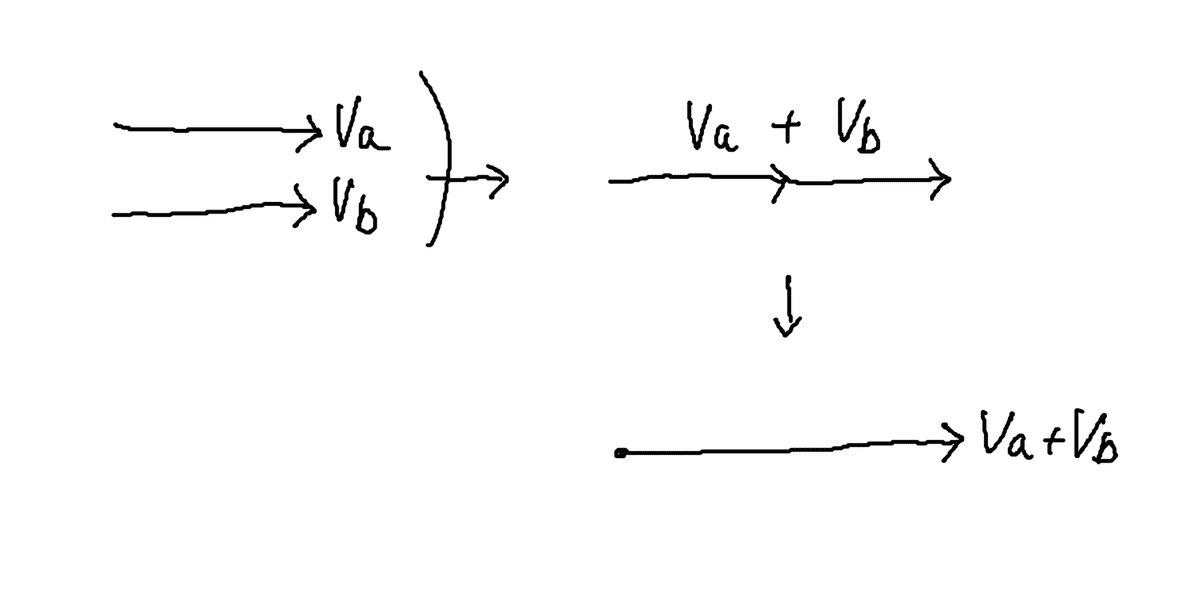
このように、同一方向・同一長さのベクトルの和ですから、向きは同じまま大きさだけ2倍になります。合成電圧もその通り、100Vと100Vの和は200Vということになります。
次は180°逆の場合。VaとVbを足すと、ベクトルが「行って戻って」となり合成値は常にゼロです。つまり、電圧はゼロとなります。
最後に、VaとVbに90°の位相差がある場合です。

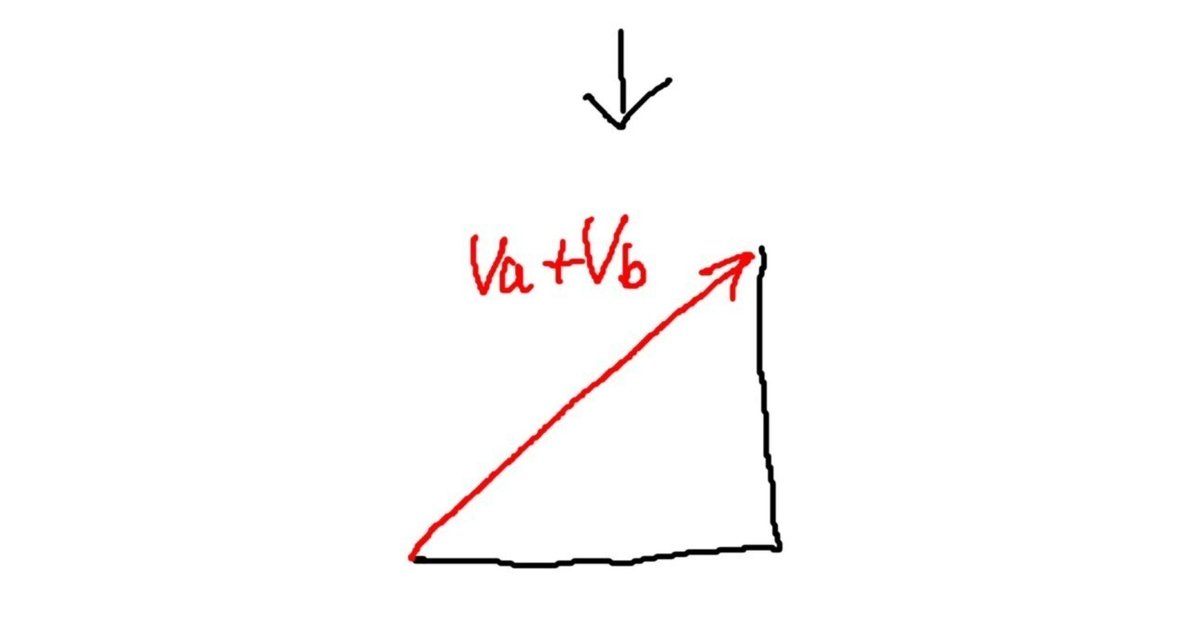
このように作図すると、三平方の定理により合成ベクトルの長さは√2倍、つまり141Vとなります。また、合成ベクトルのスタート地点は、0°でも90°でもなく、45°の点から始まることがわかります。これが、前々回に描いた

この図となるわけでした。
交流波形のフェザー表示
今回・前回・前々回と話してきたように、同じ「交流100V・50Hz」といっても、波形のタイミングが異なれば性質が全然違う、ということがお分かりいただけたかと思います。では、それらの違いを「交流100V・50Hz」だけではなく、何か表現する方法がないでしょうか?
はい。ありまーす。
そういえば某小保方女史は、私の高校時代の後輩に当たるんですな…
そのために考え出されたのが「フェザー表示」という方法です。これは、
基準となるタイミングに対して、その波形がどれだけ位相差を持っているのかという情報を、角度の記号「∠」を使って表す
という記述方法です。
例えば、最初の、位相差のない二つの波形であれば、
Va=100∠0° [V]
Vb=100∠0° [V]
のように表します。「50Hz」という周波数の情報が消えてしまったのではないか?と思われるかもしれませんが、周波数の異なる波形を足すことはできないので、この表記方法を使う場合は、「双方の周波数は等しい」という暗黙の了解があるのです。
周波数の異なる交流を直列接続するような場合は、電気のおはなしその23で紹介した重ね合わせの原理を用いて、それぞれ独立した値として別個に計算します。
二つ目の、互いに180°の位相差がある波形の場合は、
Va=100∠0° [V]
Vb=100∠180° [V]
三つ目の、90°の位相差がある波形の場合は、
Va=100∠0° [V]
Vb=100∠90° [V]
と表現します。
では最後に質問。90°の位相差がある電圧100Vの波形の合成結果は、フェザー表示ではどう表現されるでしょうか?
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
答えは、141∠45° [V] でした。
以上。
