積（んでみると）分（かる）

　日差しの気持ちいい晴れやかな朝、オフトンからさわやかに積分のお話をお送りいたします。

　ということで、

の続きです。

●変化率と面積

　それでは、「縦×横」と、「変化率から元のグラフを求める」事がどうつながるか？

[図1]

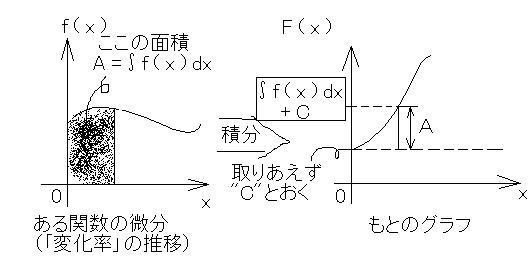
　結論から言ってしまうと、上図の左側のグラフがある関数の「微分」、

すなわち変化率の推移

（→これについては

を参照）

を表すとすると、その

スプレーをかけた部分の面積が右側のグラフの"A"部分の高さになる

と言うことです。で、この"A"を、

f ( x ) の「積分値」と呼び、∫f ( x ) dx で表す（計算する）

と言うことです。（「言うことです」が多いなぁ。。。）

　で、「不定積分」と呼ばれるものには、

積分定数（初期値）"C"

と言うのが出てきます。これは、積分して求まった値"A"というのは、

もとのグラフが「どれだけ変化したか」

しか表さないのであり、

「どの値から変化したか」が分からないので取りあえず"C"とおこう

と言う意味なのです。（"C"は、Constant「定数」の頭文字です。）

「とりあえずビールで！」

みたいなノリですね。

　だから、積分して定数"C"が出てくると言うのは話が逆なんですね。

　さて、問題は

なんで面積"A"が「元のグラフの変化」になるのか

ですが、考えやすいように、下のような簡単なグラフで実際に「積分」をしてみましょう。（難しい計算は出てこないので大丈夫です。）

[図2]

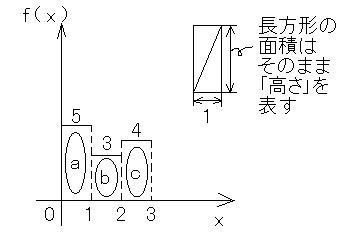
　上の図の場合は、もともと底辺が"1"に揃えてあるので、

面積 = 高さ

となるので、これよりただちに、

xが"1"進むごとにどれだけ増えるか

がわかります。すなわち「元のグラフ」を画けば、以下のようになります。

[図3]

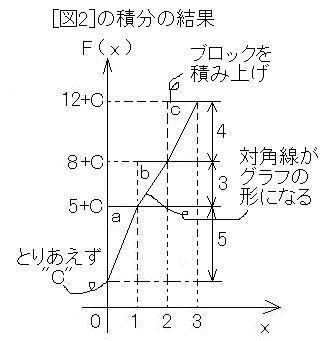
　はい、まずは「積分定数」を

「取りあえず"C"とおく」

です。ここで、

求めた面積の分、xが"1"進むごとにグラフが登る

と考えても良いのですが、ここでは

面積がそのまま高さ

だったので、

[図2]の (a), (b), (c), をブロック

と考え、図のように対角線を引いて、それをどんどん積み上げて行く

（正確には、下のブロックの「右上のへり」と、上のブロックの「左下のへり」を階段状にくっつける）

と考えても良いですね。

　それでは、

底辺が"1"でない場合はどうすんだ？

ということですが、そろそろ二度寝の時間なのでまた次回！