細かく刻んでまっすぐと見る

　どもです。白井でごぜます。どこの人だよ。
　最近、外に出るときには極力、服を着るようにしています。

　てことで、積分の

の続きです。

●底辺が"1"でない場合もタテ×ヨコ

　前回は、f ( x ) のグラフのブロックの底辺が1の時は、そのまま

（ブロックの高さ）＝（xが"1"進んだ時の元のグラフF ( x )の変化）

とできて、それは丁度ブロックを積み上げたような形になるという話でした。そこで今日は、

　ブロックの底辺が「まちまち」だった場合

についてお話します。

[図1]

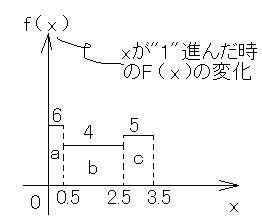
　上のf ( x )を積分して、元のグラフF ( x )を求める事を考えます。

　(a)の部分を見てみると、f ( x ) は"6"ですが、この値と言うのは飽くまで

「xが"1"進んだ時F ( x )が"6"増える」

という意味で、この場合は

xの進みが"0.5"なので、F ( x )の増分は

"6"に"0.5"を掛けて"3"

と言う事になります。わかりやすいように、

f ( x )を「時速」、xを「時間」

としてみましょう。すると、

求めるF ( x )は「距離」

になりますね。

　(a)の部分では、時速6km/hで進んでいる事になります（おそ！）。で、xが"0.5"進んでいるわけですから、6km/hで0.5時間（30分）走ったことになります。すなわち、距離F ( x )は、

6km/h×0.5h = 3km

という事ですね。（とても当たり前の事を、くどく言っているだけです。）このとき、この計算というのは、

縦が"6"、横が"0.5"の長方形(a)の面積

を求めた事と同じになります。同様に、(b)(c)を求めてグラフを書けば、下のようになります。

[図2]

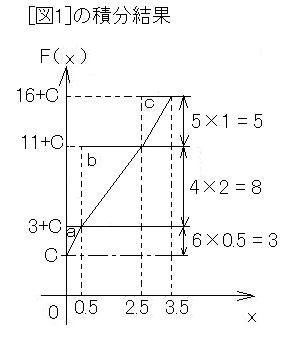
　まずは例によって、「取りあえず"C"」でしたね。そして、

a：xが"0.5"進む間に、"6×0.5 = 3"上昇

b：xが"2"進む間に、"4×2 = 8"上昇

c：底辺"1"なので、そのまま"5"上昇

になります。これらは全て、「縦×横」になっていますね。

●「ブロックの積み上げ」で考える

　さて、これを前の例でやったように、「ブロック積み上げ」で考えるとどういうことになるでしょうか。

　何度も言うように、(a)のブロックで考えてみると、f ( x )の"6"という値は、xの進みが1の時のF ( x )の増分です。つまり、

(a)のブロックの底辺がもし1だったら、高さ"6"がそのままF ( x )の増分であった

わけです。実際には(a)の底辺は"0.5"なので、

その分縮めたブロックの高さ

がF ( x )の増分を表す事になります。（下図）

[図3]

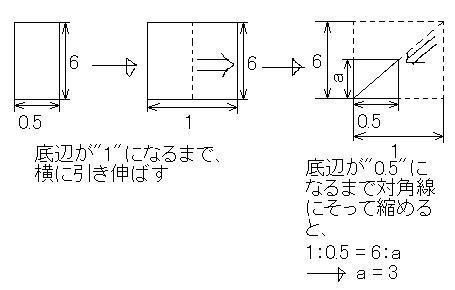
　(b)のブロックは、逆に

底辺が"2"から"1"になるまで縮めてやってから、対角線にそって引き伸ばし

てやればよいのです。

　要するに「接線」からグラフを求めている

　ここで面白い事が分かります。それは、

f ( x )の「高さ」 = F ( x )の「高さ」／「底辺」

となっていることです。つまり、f ( x )を「F ( x )の変化率」と見た時は、f ( x )というのは

あらかじめ「底辺」で割ってある値

なのであり、「縦×横」を利用して「f ( x )のグラフ」と「x軸」に挟まれた部分の面積を求めたものが、F ( x )の高さ（すなわち前回の最初の図）であるわけです。例えばさっきの例で、

「時速」(f ( x )の高さ） = 「距離」／「時間」（F ( x )の「高さ」／「底辺」）

ですね。考えてみると何ともバカみたいな話ですが、積分はこれが核になっていて、これ以上のものではないのです。

　つまり「積分」とは、

f ( x )を、F ( x ) の「微分値」すなわち、グラフf ( x )をF ( x )の「接線」と見て、元のグラフF ( x )の形を求める

という事に相当します。

●一般の曲線のグラフについて

　さて、それでは

曲線のグラフについてはどうなのか？

ですが、

でやったように、

細かく区切って「長方形」に見なす

わけです。

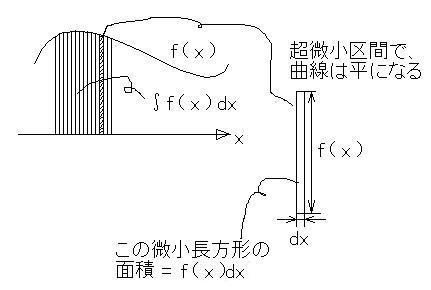
　すなわち、上図のように求める面積の区間を細かく分割してやります。こうすると、

曲線が「区分的」に平

になり、求める区間の面積は

長方形の面積の「和」

になり、「縦×横」に帰着できるわけです。このとき、

"⊿x"を極限まで微小に区切った量を、"dx"と書く

ことにして、この

極めて微小な面積"f ( x ) dx"を足し合わせて行くことを、"∫f ( x ) dx"と書く

ことにしたわけです。

●ちょっと発展的な話

　この、

微小区間で平と見なす

という手法は、微積分の常套手段であり、例えば「全微分」というは

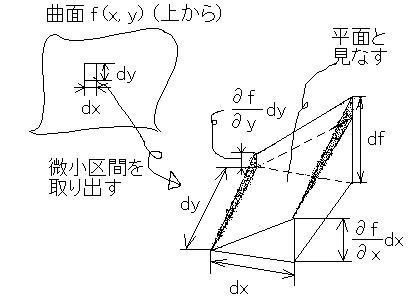
d f (x, y) = (∂f /∂x ) dx + (∂f /∂y ) dy

ですが、これは「曲面の高さf (x, y)」の

微小区間"d f(x, y)"を平面と見なす

事で、下図のようにして考えているわけです。

●まとめ

　こうして「面積」と「変化量」という２つのものは

実は数学的に同じ事

であり、「微分」と「積分」が

互いに逆の演算

であることが把握され、ニュートンとライプニッツによって「微分積分法」の基本定理が確立されたのは、17世紀末の事でした。

　以上で微分と積分の話は終わりです。めでたしめでたし。（何が？