
中学受験算数『容器と水量攻略法』
こんにちは。三上圭です。札幌の塾で中学受験の算数を指導しています。
今日のテーマは『容器と水量』です。
このブログで扱っている問題とその解答、解説動画のまとめページはこちらからどうぞ。(まとめページの教材にはブログで扱えなかった問題も入っています!)
このテーマで大切なことは
・正面から見た図を書いて、条件を整理する
です。いずれの解説でも、正面から見た図を用いて説明しています。
入れたものが完全に水の中に沈む問題
たて20cm、横30cm、高さ18cmの直方体の形をした容器に、16cmの深さまで水が入っています。この容器に石を完全に沈めたところ、水が300cm3だけこぼれました。
(1)この石の体積は何cm3ですか。
(2)(1)のあとに、沈めた石を取り出しました。石を完全に取り出したあとの水面の高さは何cmですか。ただし、石を取り出すときに水はこぼれなかったものとします。
※以降、cm3は立方センチメートル、cm2は平方センチメートルを表します。
正面から見た図に整理しましょう。
(1)

この図では、横の長さを底面積の値で考えると便利です。
いまは20×30=600cm2 を横の長さにしています。
あと1200cm3入る状態で石を入れると300cm3こぼれるのだから、この石の体積は1500cm3だとわかるでしょう。
ここで完全に沈むときのポイントですが
『ものが完全に沈む問題は、同じ体積の水を入れたと考えて良い』
ということです。もうちょっと簡単に言うと
体積1500cm3の石を入れることと、体積1500cm3の水を入れることは、結果として変わらないということです。
(2)今度は石を取り出します。
完全に沈んでいた石1500cm3は、水1500cm3と変わりません。
なので、満水の状態から水を1500cm3取り出せばOK。

図のようになり、15.5cmが求められます。
と、いろいろと書きましたが、解説動画がありますのでこちらをどうぞ。
では次の問題に進みます。
入れたものが水面からはみ出している問題
容器と水量で多いのはこの出題だと思います。棒やおもりを順番に入れていく問題です。
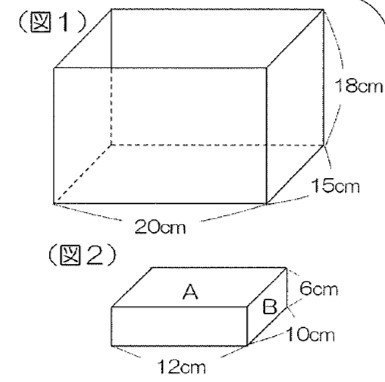
図1のような直方体の水そうに、水面の高さが6cmのところまで水を入れました。
(1)(図2)の直方体をAの面が真上を向いた状態で水そうの底につくまで入れました。このとき、水面の高さは何cmになりますか。
(2)(図2)の直方体をBの面が真上を向いた状態で水そうの底につくまで入れました。このとき、水面の高さは何cmになりますか。
(1)
Aの面を上に向けると、(図2)の直方体は完全に沈みます。同じ体積の水を入れたのと同じ!と考えてOKです。
つまり12×10×6の体積の水を、底面積が20×15の容器に入れればいいから
(12×10×6)÷(20×15)=2.4cm上がる。
6+2.4=8.4cmが答えです。
(2)
今度はBの面を上に向けます。(図2)の直方体は一部が水面から上にはみ出すことになります。こんなときは
『どこかとどこかの体積(図の中では面積)が同じ!』
と考えていきます。
『押しのけた部分の体積』=『見かけ上増える部分の体積』
と言葉で書いても難しいので、図にすると「同」と「じ」の部分のことを言っています。
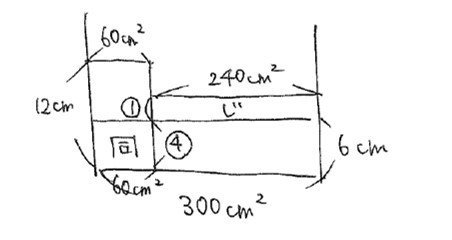
もとは水があったところに直方体が入るので、その部分の水がおしのけられて『ニョロ』っと右上に出てくるイメージです。
(このとき、入れるものはどちらかの端に寄せて書くとイメージしやすくなると思います!)
ここで図の「同」「じ」の部分の横の長さの比が1:4だとわかっているので、たての長さの比は4:1になります。(面積が同じだから、たてと横の比が逆比になる)
それぞれ①と④と置くと、④が6cmとわかります。水面が上昇した①の分は①=6÷4=1.5cmですから、水面は全部で6+1.5=7.5cmになりますね。
※アップ当時、⑤=6cmで①=1.2cmという誤りがございました。大変申し訳ございません。現在は正しい表記になっております。
動画もぜひご覧ください!『速さ』や『容器と水量』のように変化を追いかける問題では、出来上がりの図だけを見ても意味がわからないことがあります。順を追って「なぜこういう図になるのか」を理解していくことが大切だと思います!
では3問目。ぜひ取り組んでもらいたい重要な問題です。
入れたものが水面からはみ出している問題(練習問題)
底面積が250cm2で、深さが20cmの円柱の容器と、底面積が50cm2で、高さが15cmの直方体のおもりが2個あります。いま、容器に深さ10cmまで水を入れました。
(1)直方体のおもり1個を容器の底に立てると、水の深さは何cmになりますか。
(2)(1)のあと、おもりもう1個を容器の底に立てると、水の深さは何cmになりますか。
(解説は省略します)
答えは(1)12.5cm (2)16 cm です。
(2)が分数になった人は、なぜ間違えたのか動画でチェック!
容器を傾ける問題
容器と水量には、いままでのように「物を沈める・入れる問題」のほかに、今回扱う「容器を傾ける問題」や「じゃ口から水を入れていく問題」などがあります。
図1のように一辺が12cmの立方体の形をした水そうに5cmの深さまで水が入っています。この水そうを、底面の1つの辺を床につけたまま水がこぼれないように傾けたところ、図2のようになりました。
(1)図2の χ の長さは何cmですか。
(2)さらに水そうを傾けていくと、180cm3の水が水そうからこぼれて、図3のようになりました。図3のyの長さは何cmですか。

(1)
この容器の底面積は12×12=144cm2なので、(図1)で正面から見たときの水の面積は144×5=720になります。
これは(図2)で見ても同じなので、144× χ ÷2=720と考えてOKです。
あとは計算すると、χ=10cmと求められます。
(2)
180cm3がこぼれたということは、(図3)で見えている面積は
720-180=540 になります。
1つ注意して欲しいのは、yは横の長さであって底面積ではないことです。容器の奥行、高さがともに12cmとわかっているので、
底面積(y×12)×高さ(12)÷2=見える面積(540)と考えて
y×12×12÷2=540 を計算すると y=7.5cm になります。
最後に
容器と水量では
・正面から見た図に条件を整理する
ことが解法の第一歩です。積極的に図を書いて頑張っていきましょう!
私が通常授業を担当している塾の情報は以下のリンクからどうぞ。
ツイッターでもブログの更新や動画アップロードのお知らせをしています。
→中学受験情報や日々の生活の様子をのんびりつぶやいています。フォローや「いいね!」など、よろしくお願い致します!
この記事が気に入ったらサポートをしてみませんか?
