
【算数・数学】引き算→割り算→微分
こんばんは、Junです。
今回は、引き算と割り算、そして微分について解説していきたいと思います。
引き算(減算)
引き算とはある2つの値の差を求める計算です。
例)Aさんは、自宅から直線距離で1km地点にあるスーパーで買い物をした後、自宅から3km地点にある公園に行きました。
Aさんの自宅とスーパー、公園が同一直線上にあるとき、スーパーから公園までの距離を求めなさい。

解)Aさんの自宅とスーパー、公園は同一直線上にあるので、

3 - 1 = 2
答えは2kmです。
割り算
割り算は、あるカタマリをいくつかのグループに分ける計算方法です。
例)10個のリンゴがあります。5人で分けるとき、1人当たりの個数を求めなさい。

解)10個のリンゴを5人に分けるためには、10個のリンゴを5つのグループに分けてあげる必要があります。
1つのグループの中には、リンゴが2個入ることが分かります。
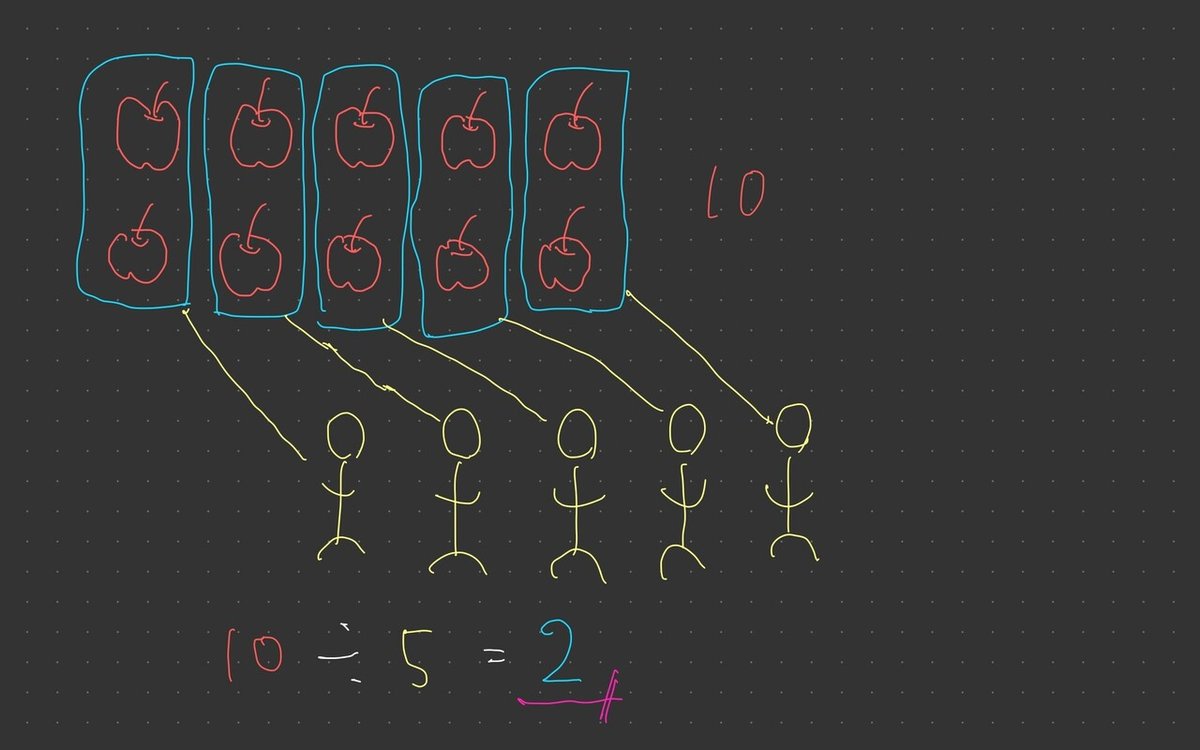
これを式にすると、
10 ÷ 5 = 2
よって、1人当たり2個となります。
また、割り算は単位時間あたりに進む距離を求めることにも使われます。
例)ある自動車が一定の速さで直線上を走行しています。300km先にたどり着くまで3時間かかりました。この自動車の速さは時速何kmですか?
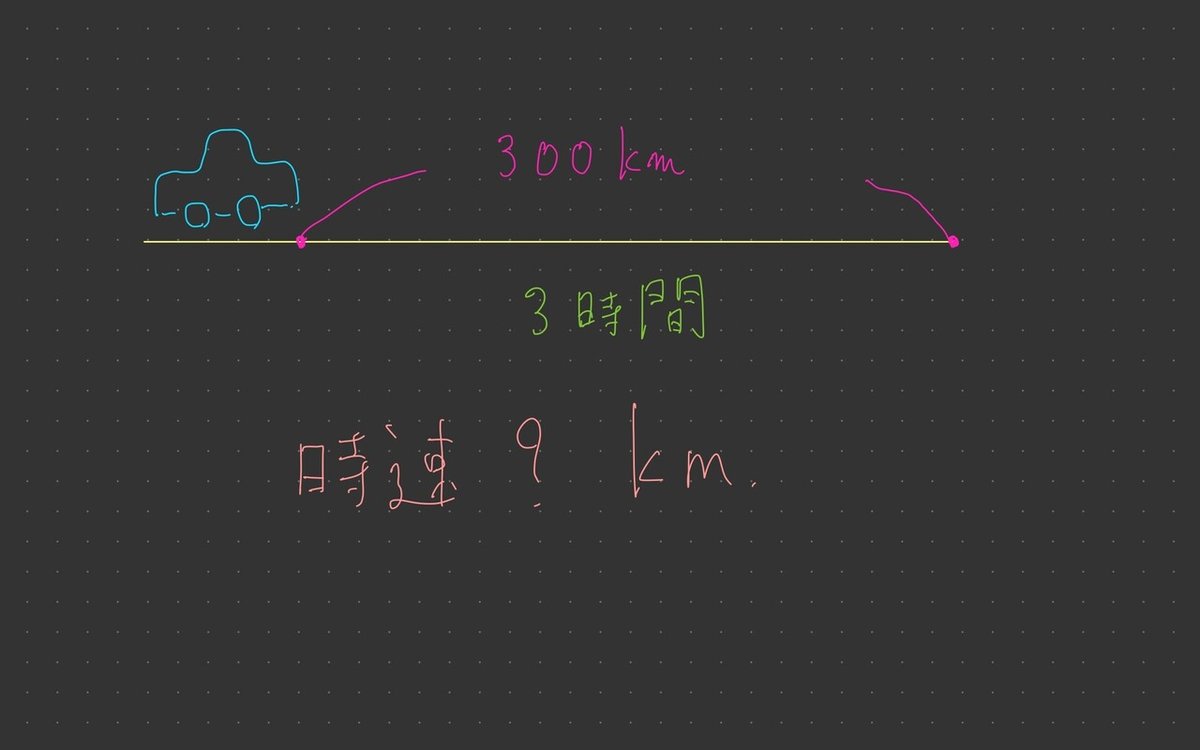
解)この自動車は300km走行するのに、3時間かかったので、1時間当たり何km走行したことになるかを計算すればよいので、
速さ = 距離 ÷ 時間
300 ÷ 3 = 100

よって、この自動車は時速100kmで走行していることが分かります。
この様子を、横軸に時間、縦軸に距離をとってグラフにしてみると、以下の通りになります。

このグラフにおける傾きが速さを表していることが分かります。
微分
先ほどは、速さが一定の例を挙げましたが、今度は速さが一定でない場合を考えます。

このように速度が変化する場合の、次の2点間の平均の速さvを求めます。

この時、2点を結ぶ直線の傾きを求めればよいので、

となります。

となります。
では、t = t0における瞬間速度を求めるにはどうすればよいでしょうか?

そこで、このように考えます。

Δtを限りなく0に近づけます。
それを、このような式で書きます。

このx'(t0)を、関数x=x(t)のt=t0における微分係数と言います。
そして、この式を任意の実数tで定義した、

を、関数x=x(t)の導関数といい、この導関数を求めることをxをtで微分すると言います。
微分と聞くと難しく聞こえてしまうかもしれませんが、冒頭の引き算・割り算の延長であると考えれば、それほど難しいものではないのではないかと思います。
微分は、大学受験だけでなく、物理学や統計学などでも使われ、IT分野では、機械学習などにも使われているので、「AIを作りたい」、「機械学習や深層学習をやりたい」という方には重要な単元となっておりますので、押さえておいていただければと思います。
ちなみに、解説に使用したアプリは、GoodNotesというものを使用しております。
是非使ってみてください。
この記事が気に入ったらサポートをしてみませんか?
