主成分分析と因子分析について
前回多変量解析の中で一番有名(?)の重回帰分析についてやっていきました。今回は主成分分析について見ていきます。また多変量解析とはなんぞやという方は前回の記事の前半に軽くまとめましたのでご覧ください。
今回の内容は次の通りです。
・主成分分析とは
・因子分析とは
・主成分分析と因子分析の違い
・pythonで実践
1.主成分分析(principal component analysis)とは何か
簡単に言えば特徴量の縮約です。例えば現代文・小説・古文・漢文の成績にそれぞれ相関があれば、まとめて国語力にまとめても大丈夫ですよね。また国語・英語・社会を一つのグループに、理科・数学をもう一つのグループにそれぞれまとめれば、文系力・理系力という新たな指標として測定することができると思います。これらが主成分分析でできます。またそれ以外にも役割があります。それは直感的に理解できやすくする(つまり可視化できる)ことです。人間は三次元までしか頭で理解できません。試しに二次元のグラフを浮かべてみてください。簡単ですよね。では100次元のグラフを想像してみてください。ほぼ不可能だと思います。せいぜい3次元が限界だと思います。まとめます。また機械学習には次元の呪いと言うものが存在します。これは計算に莫大に時間がかかるだけでなく、未知のデータに対応できなくなる恐れがあります。
主成分分析の役割
・データの特徴抽出
・データの次元節約
・多次元特徴量の可視化
では主成分分析に深く入っていく前に軽く流れを紹介します。
・データの標準化・基準化
・分散共分散行列の計算
・固有値・固有ベクトルの算出
・大きい方を第一主成分の固有値として計算
今回は事前に用意した成績データを使用します。

まず主成分分析をするに当たってデータを標準化する必要があります。標準化とは平均を0、分散を1にすることです。またデータの単位が異なっていたら揃えてください。(cm→mなど)


軽く主成分分析についてみてみましょう。今回もまずは二つの変数で考えます。答えは散布図に直線を引きます。この時この直線は分散が最大になるように引きます。この時の直線を第一主成分軸と呼びます。なぜ分散が大きい方が良いかと言うと情報を少なく失わずに済みます。次に二番目に分散が大きい所にもう一本引いてみます。これを第二主成分軸と呼びます。この第二主成分軸は第一主成分軸と直角になるように引きます。またこの主成分軸の作成する目安として、固有値が1以上、累積寄与率が80%とします。(あくまで目安なので自分が納得できるように設定してください。)この時の主成分軸の式を次のように表すことができます。またこの式のことを主成分と言います。また第一主成分軸は大抵総合力を示します。(場合による)

ではこの主成分軸を引けばいいのでしょうか。分散を最大化する必要があります。ここで分散の公式再確認してみます。

これを展開してみるとxの二乗がn個出てきます。しかしこのままだと無限にデカくなってしまうので条件を加えます。これをラグランジュの未定乗数法と言います。(詳しく知りたい方はこちらを参考にしてください。)これは拘束条件がある関数で極値を求めるテクニックです。軽く極値の話をしますので、飛ばしても問題ありません。
極値とは局所的に大きくなったり、小さくなったりする場所のことです。最大値と最小値と何が違うのと言うと、最大値・最小値は関数の中で一番大きい(小さい)場所を指します。一方三次元以上の関数ではいくつか凸凹な関数になります。その箇所が極値です。分岐点的な感じです。その極値と言う名の分岐点で減少から増加、増加から減少していると思います。
ではそのラグランジュの未定乗数法を用いて極値(今回の場合は分散を最大化する値を求めていきます。)この方法を使うに当たってλと言う文字を使ってそれぞれの文字x1・x2・....xn・λで偏微分します。また各式に0と置くのは極値を求める上では必須条件になります。微分し終わったら連立方程式の形に変換します。行列で表すと次のようになります。ここであることに気づいた人は天才です。左辺が分散共分散行列になっています。これは各変数間の分散と共分散が入っています。左上と右下が分散、右上と左下が共分散となっています。またこの行列自体が固有ベクトルの式になっています

試しに分散を別で求めてみましょう.

同じになりました。
ここで軽く固有値について解説します。固有ベクトルとは行列(仮にA)を掛けてもλ倍されるだけで方向が変化しないベクトルのことです。またそのλのことを固有値と言います。固有値は分散がどれだけ広がっているかを示しています。
この固有ベクトルの式を解くとλが二つ求めることができます。先程も言いまいしたが第一主成分軸は大抵総合力を示すことが多いため、第一主成分軸のλは大きい方になります。では残ったλは何でしょう。今回は第二主成分軸まで求めるつもりなので、残ったλは第二主成分軸の固有値になります。また第一主成分軸と第二主成分軸は直交すると言いました。お互いの主成分に対応する係数をかけて、足すと0になります。つまり90°で交わっていることになります。
では次に寄与率と累積寄与率を求めていきます。ここでの寄与率はその主成分がデータの何%を説明できているかを示します。累積寄与率とは第一主成分からある特定の主成分によってデータ全体の何%を説明できるかを示すものです。これは次のように定義されます。総分散は固有値の数です

なぜ寄与率を求めるのでしょうか。データの縮約をすることでいくつかデータが漏れてしまいます。要約できたもののそのデータが全体のたった数%しか説明できていないと意味がありません。
また先程はデータを標準化して求めましたが、実はデータを揃えなくても求める方法があります。分散共分散行列ではなくて、相関行列を求めても同じになります。相関行列とは次のようなものです。
これで主成分分析の理論は終了です。次は因子分析も一緒にやっていきます。
2.因子分析とは
因子分析とは多変量データに潜む共通因子を取り出すための手法です。例えば英語ができる人にはどのような要因が考えられますか。論理的思考力や記憶力、またはコミュニケーション力など様々な要因が考えられます。しかしこれらの因子は実際には観測することはできません。また因子にも種類があります。
・共通因子:分析対象となる変数の組に共通する因子のこと
例:英語と数学の場合、考えられる共通因子は読解力・論理的思考力など
・独自因子:各変数に独自に関わる因子のこと。
例:英語の場合、それぞれの単語の知識(英単語や慣用句、数学の用語・記号)や数学だったら計算力
また簡単に用語を紹介します。
・観測変数:調査や実験などによって直接測定した変数のこと
・潜在変数:直接測定はしていないが、観測変数のパターンによって説明できるような変数。
因子が分かったところで因子分析の流れそ紹介します。
・共通因子の数の決定
・因子負荷量(係数)の算出
・因子結果を見る
・因子軸の回転
・因子の解釈(ごめんなさい、まだ理解していないので加えていません。)
・因子得点の解釈
また因子分析には二種類の方法が存在します。探索的因子分析と確認的因子分析(検証的因子分析)です。前者は因子と観測変数の間の関係について、先行する仮説や制約を分析時に考えず、観測によって得られた観測変数のみから相関係数を計算し、観測変数間に相関関係をもたらす因子は何かを推定する手法のことです。一方で探索的因子分析は先行する理論を元に、因子の数や意味、環境変数の関係をあらかじめ規定しておいた仮説を作って、その仮説が正しいかどうかを検証する手法のことです。要は因子を予め推定するかどうかの違いです。
まず共通因子の数の決定だが、これには様々な手法があるので定番の手法を紹介します。
・カイザーガットマン基準:固有値が1以上の因子を採用する
・スクリー基準:固有値の大きさをプロットし、推移がなだらかになる前までを抽出する。
・寄与率が50〜60%以上になる因子数を推定する。
・解釈が可能な因子構造を採用する
一番目と三番目は主成分分析の主成分の数の求め方と同じですね。初めからこれと言うのはないので色々な手法を試してみてください。(正解はないので試行錯誤してみてください。)
次に因子負荷量を求めます。これは重回帰分析の編回帰係数と同じで係数を意味しています。これが大きい程影響力が強いと言うことになります。因子負荷量を求めるには固有値や固有ベクトルを求める必要があります。では主成分分析の時に求めた相関行列を借ります。

上の二つは固有値で下の四つが固有ベクトルです。この固有ベクトルと固有値を使って因子負荷量を求めます。次の公式を用います。

上の公式を使って因子負荷量を求めた結果が次の通りです。(すいません上と順番が違います。)またこのように因子負荷量を求めることを主因子法と呼びます。他にも因子負荷量の求め方があって、セントロイド法や最尤法などがあります。

寄与率を調べていきます。これはその要素がデータ全体の何%を説明をしているかを示している指標でした。

総分散と書いてありますが、固有値の数と解釈して大丈夫です。(実際は相関行列の対角要素の和です。)
3.Pythonで主成分分析と因子分析
3-1.Pythonで主成分分析
さて本題です。Pythonで主成分分析と因子分析をやっていきましょう。かなり簡単です。また先程と違ったデータを使用していきます。今回使うデータは科目数と生徒数が多くなったこちらのデータです。(ある程度バイアスを加えた自作のデータです。)
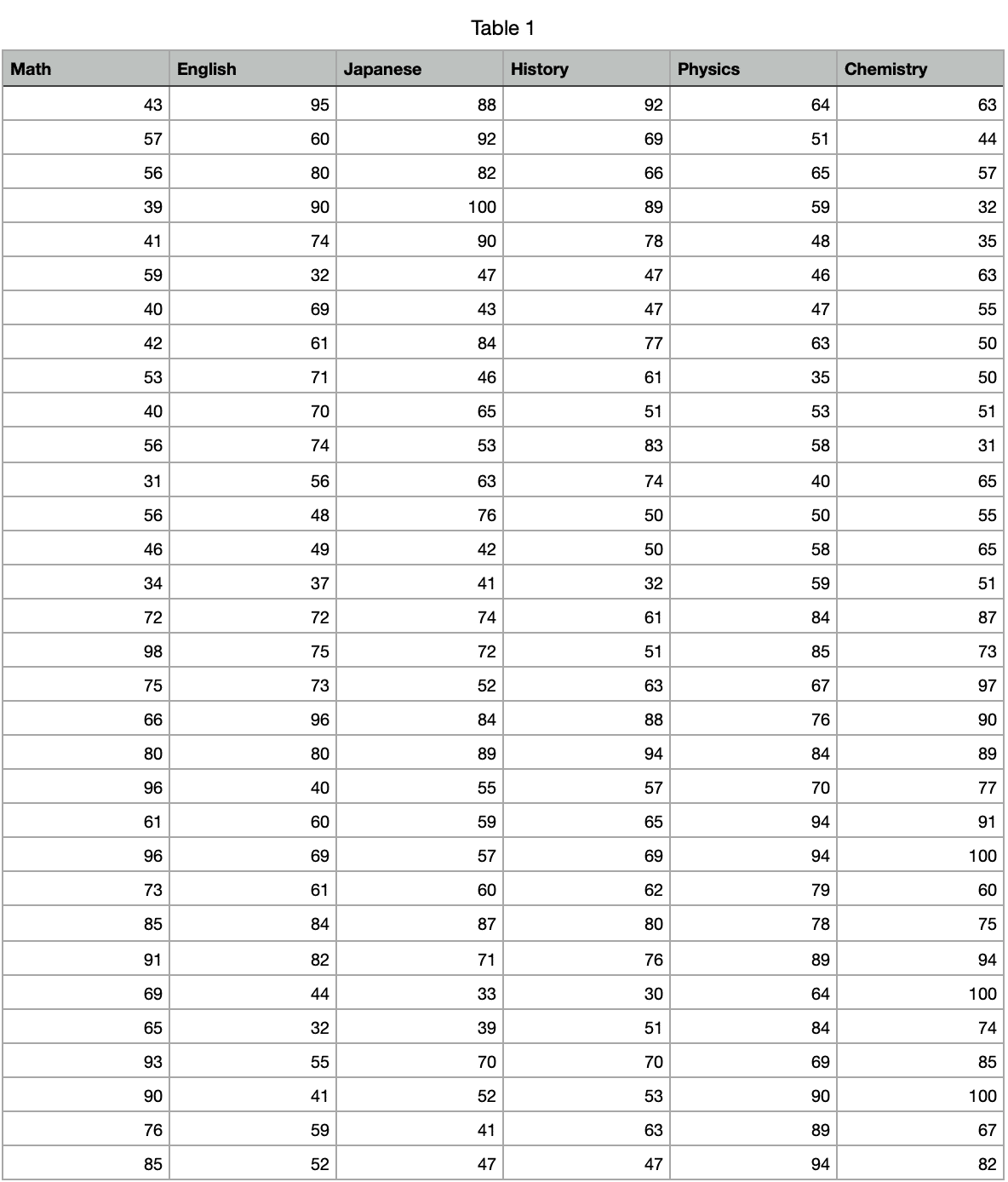
データの特徴についてみていきます。平均点は大体同じで、ばらつきも化学と数学を除けば大体同じですね。

相関も見てみます。理系科目同士・文系科目同士は強い関係がありますね。

では早速主成分分析を行っていきます。主成分分析はPrincipal Component Analysisと言い、PCAと略すことが多いです。scikit-learnのdecompositionと言う所にPCAが含まれています。呼び出したらPCAのインスタンスを作成します。その次にpcαインスタンスに先程のデータフレームを当てはめてモデルを作成します。最後にtransfrom関数を実行して主成分分析を実行します。この3ステップで主成分得点を求めることができます。簡単ですね。また一番したのコードを実行することでfit関数とtransform関数を同時に実行することができます。
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(df)
df_pca = pca.transform(df)
df_pca = pca.fit_transform(df)ずらっと沢山の数字が出てきました。これが主成分得点です。これをデータフレーム化します。多いので半分だけ出します。
df_pca = pd.DataFrame(data = df_pca, columns= ["PC{}".format(num + 1) for num in range(len(df.columns))])
df_pca #主成分得点のデータフレーム 
第6主成分まであります。
次に寄与率と累積寄与率を求めます。
ex_ratio = pca.explained_variance_ratio_
df_ex_ratio = pd.DataFrame(ex_ratio, columns=["Contribution ratio"],
index=["PC{}".format(num + 1) for num in range(len(df.columns))])
df_ex_ratio #寄与率 
第一主成分が約半分を説明しています。では次に累積寄与率をグラフ化してみます。
cc_ratio = np.cumsum(ex_ratio)
plt.plot(cc_ratio, marker="o")
plt.xlabel("PC")
plt.ylabel("Cumulative contrivution rate")
plt.show()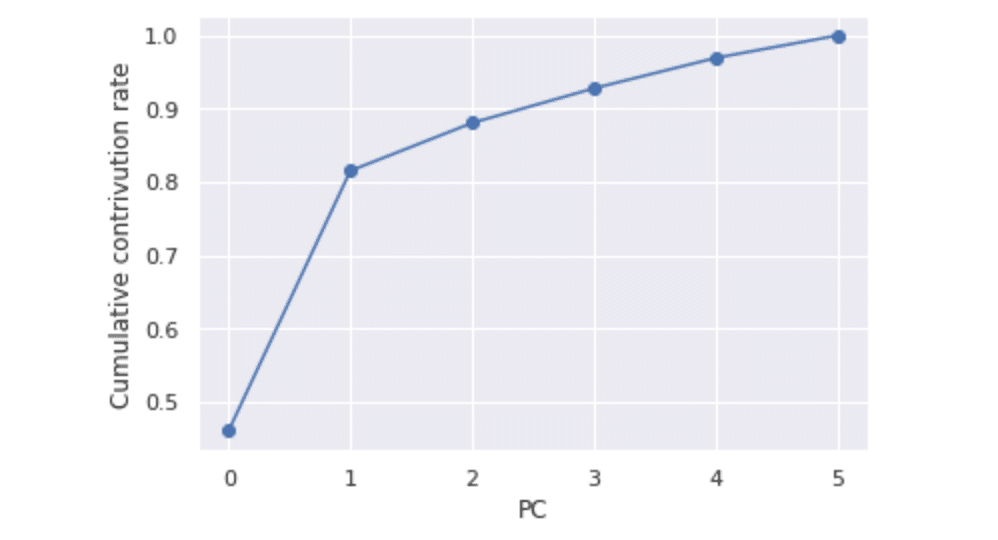
以前にも言いましたが主成分・因子の数を決める目安として累積寄与率が80%以上でした。今回は第二主成分までで大丈夫そうです。
しかし安易に断定してはいけません。必ずそうとは限らないので各自で必要な主成分を取ってください。
最後に主成分負荷量を見ていきます。
eigen_vector = pca.components_.T
pc_loading = pd.DataFrame(eigen_vector, index=[df.columns],
columns=["PC{}".format(num + 1) for num in range(len(df.columns))])
pc_loading #主成分負荷量 
それぞれの主成分を解釈していきます。(第三主成分まで)
第一主成分は数学・化学・物理(理系科目)がマイナスでそれ以外(文系科目)はプラス方向に働いています。見事に文系と理系に分かれていますね。文系科目は得意で理系科目は苦手と言う人は主成分得点が大きくなっています。
第二主成分は理系科目は少しマイナスが弱くなったのに対して、文系科目はプラスからマイナスになりました。
第三主成分は数学・国語・物理がプラスになり、英語・歴史・化学がマイナスになりました。一応取ってみましたが正直に言うとわからないです。
これらのことを踏まえてもう一度主成分得点を見てみましょう。番号が3、4の人は第一主成分得点が高いですね。得点も見てみると文系科目の点数が高く理系科目の点数が低いですね。一方下の表から三番目を見てみると一番主成分得点が低いですね。点数も確認すると理系科目が高く文系科目が低いですね。主成分負荷量を解釈することでデータの特徴が大体わかりますね。

次に因子分析をやっていきます。データは先程と同じデータを使用していきます。今度も同じscikit-learnのdecompositionからFactorAnalysisを取ってきます。また今回は因子の数を3とします。今回は因子数はモデルに当てはめる時に設定します。
from sklearn.decomposition import FactorAnalysis as FA
n_factors = 3
fa = FA(n_factors)
fa.fit(df)これで因子分析用のモデルが完成しました。では次に因子負荷量を求めていきます。
df_factor_loading = pd.DataFrame(fa.components_.T, columns=["factor{}".format(num) for num in range(n_factors)],
index=df.columns)
df_factor_loading #因子負荷量 ではそれぞれの因子負荷量を解釈していきます。まずfactor0は文系科目と理系科目とで綺麗に分かれていますね。文系科目がプラスで理系科目がマイナスになっています。
factor1では理系科目が少し増えて文系科目が大きく下がりました。
factor2では数学と化学が下がり、それ以外は上がっていますね。

最後に因子得点を求めていきます。これを調べることで各生徒がどのような要素を持っているかをみることができます。
factor_score = fa.transform(df)
factor_scores = pd.DataFrame(factor_score, columns=["factor_{}".format(num) for num in range(n_factors)],
index=df.index)
factor_scores #因子得点 factor0を見てみると半分を境にプラスからマイナスになっています。半分からしたは文系科目に弱く、半分から上は文系科目に強いことが分かります。
次にfactor1を見てみると半分から上は半分からしたよりもマイナスの人が比較的多いです。先ほどの因子負荷量の解釈から理系科目が強い方がプラスだということが分かります。
またそれぞれの生徒同士で比較もできます。factor0で比較するなら大き方がより文系科目の点数が良いことも読み取れます。

この記事が気に入ったらサポートをしてみませんか?
