
感染者数の波は接種数の波によって引き起こされる
まず、2021年の世界の感染者数のグラフを見てください。これは世界全体で毎日何人の感染者が出ているかを表したものです。(100万人あたり)
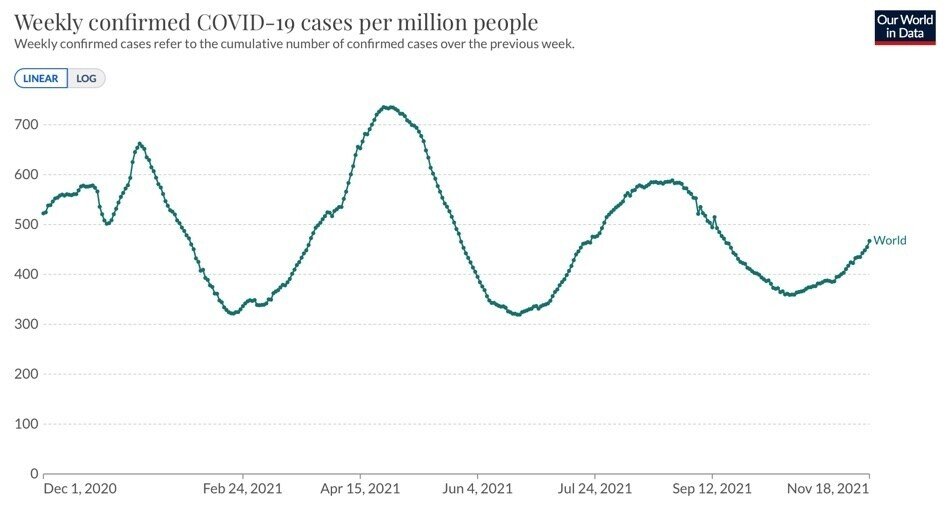
次に、2021年の世界のコ○ナ〇〇チン接種数のグラフです。1日ごとに世界全ての国で〇〇チンが接種された数を足したものです。(100人あたり)

この二つを重ねてみます。(青い線が接種数、緑が感染者数)
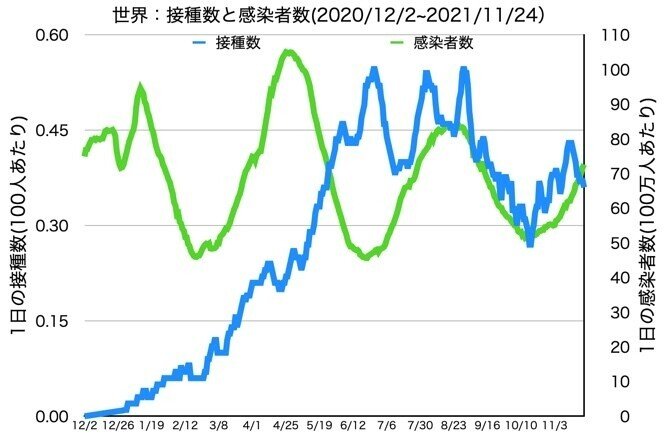
この2本のグラフに『相関』はあるでしょうか?
一見して「ない」と思われる人もいるかもしれません。
「『相関』って何?」
と思った方は、以下をどうぞ。
「そんなの知ってる」あるいは「知らないけど、知らなくていい」という方は、次の見出しまで読み飛ばして行ってください。
相関というのは、お互いの数字の関係の強さのことです。
一つの数字と相手の数字に関係がある時、「相関がある」と言います。
お互いの数字に関係がない時、「相関がない」と言います。
人間関係にも恋人や夫婦のようなすごく親密な関係から、1回あったことがあるだけのような関係までいろいろあるように、相関にも程度があります。数字同士の関係が強い時『相関が強い』、関係が弱い時『相関が弱い(低い)』と言います。
例えば、👇の緑のグラフと青のグラフには関係があると思いますか?

☝️このグラフ1は一緒に動いていますから、誰が見ても2本の線には関係がある、つまり『相関がある』とわかると思います。これは例えば、ある店員が1人のお店にいる人の数とお客の数です。店には店員が必ず一人いるので、いる人の数はお客+1人になります。
では次、👇次のグラフは?相関があるでしょうか?

これは例えば、サイコロの目と子どもの通信簿の成績です。
お互い関係なくバラバラに動いています。こういうお互いに全く影響を受けず関係がないことを『相関がない』と言います。
『相関がある』時、『相関』には大きく分けて2種類あります。
最初のグラフは、客の数が増えれば店にいる人の数も一緒に増えます。客が減ったら店にいる人の数も減ります。

こういう片方が増えたらもう一方も増え、片方が減ったらもう一方も減ると決まっている関係を『正の相関』と呼びます。
次に、こんなグラフをみてみましょう。

☝️このグラフは、例えばあるお寿司屋さんで毎日5人限定の海鮮丼を食べた客を男女別に数えたグラフです。
食べた男性が増えれば、食べた女性は同じだけ減ります。逆に女性が増えれば男性が減ります。
このように片方が増えたらもう一方は減る、逆に片方が減ったらもう一方は増えると決まっている関係を『負の相関』または『逆相関』と呼びます。
こうした関係を、一つの数字で表したのが『相関係数』(R)です。
関係がパッと見でわからないことも多いので、相関を調べるためには散布図という図を作ります。(詳しくは省きます)
相関係数は、この散布図の点がどれだけ一直線に近く並んでいるかで決まります。
『正の相関』が強いほど、散布図は右に上向きの1直線に近く並びます。
客の数と店員1人の店にいる人の数のように、完全に右上の一直線になる時は、『相関係数R=1』です。これは最も強い相関です。

一方、海鮮丼のグラフのような『負の相関』(逆相関)では、散布図は右に下向きの1直線に近く並び、相関係数R=-1になります。これも最も強い相関です。

もう一つグラフをみてみましょう。

☝️このグラフ2は、例えばある結婚式場で、結婚したカップルの数と結婚した人の数を示したグラフです。
カップル数が増えれば、結婚した人数も増え、カップル数が減れば結婚した人数も減ります。(結婚した人はカップル数の2倍)
ですからこれは『正の相関』です。客と店にいる人のグラフのように平行ではありませんが、相手の数が決まればもう一方の数も完全に決まります。
こちらも散布図は1直線に並び、右上がりなので相関係数R=1になります。

このように、一方の数字だけで他の条件が何も入らずもう一方の数が決まる時時、相関は最も強くなり、相関係数は1か−1になります。
一方、サイコロの目と通信簿の成績のグラフを散布図にすると、各点はバラバラできれいな線に並びません。

なんとか直線を引こうとしますが、どうしても多くの点が線から離れてしまいます。
こういう時、2つの数字には「相関がない」あるいは「相関が弱い(低い)」と言います。
相関係数は『−1〜1』の間にあり、「1」に近いほど『正の相関』が強い、「−1」に近いほど『負の相関』が強い、そして「0」に近ければ相関が弱い、つまりあまり関係ないことになります。
まとめますと、
①相関とは2つの数字の関係の強さのこと
②一方が増えるともう一方も増える時、あるいは一方が減るともう一方も減る時、正の相関と呼ぶ。
③一方が増えるともう一方は減る時、あるいは一方が減るともう一方は増える時、負の相関と呼ぶ。
④相関が強いほど、散布図は一直線になり、正の相関では右上がり、負の相関では右下がりの直線に近くなる。
⑤相関の強さを数字で表したのが相関係数Rで、Rは1〜ー1の間にあり、1に近いほど正の相関、−1に近いほど負の相関が強く、0に近いほど相関がないことを意味する。
接種数と感染者数の関係
さて、ここからが本題です。
世界の接種者数と感染者数に相関はあるでしょうか?

全体を一見すると、それぞれは関係なくバラバラに動いているように見えます。
実際に散布図を作ってみると、全体の相関係数は『R=-0.1766』で、ほとんど相関はないことがわかります。

しかし、9月以降に限ればどうでしょう?

かなり一致して増減しているように見えないでしょうか?
9月以降の相関係数を調べると、相関係数『R=0.8278』。かなり強い正の相関があることがわかります。

もし〇〇チンが「感染を防ぐ」ならば、本来、接種数と感染者数には『負の相関』があるはずです。ところが9月以降に限ってみれば、実際には接種数と感染者数には強い『正の相関』がある。これはつまり、接種が増えたら感染者が増えた、あるいは、感染者が増えたら接種が増えたことを意味しています。
感染者が増えれば、危機意識が高まって接種する人が増えるからだ。
そう思われるかもしれません。
相関関係は因果関係ではありません。相関があるだけでは、感染者が増えたから接種が増えたのか?接種が増えたから感染者が増えたのか?どちらかわかりません。
次に、接種数と前後の日の感染者数の相関を調べてみましょう。

すると、接種数は6日後の感染者数と最も強く相関し、相関係数はなんと『R=0.9088』という高い数字になりました。これはつまり、感染者数はほとんど6日前の接種数によって決まってくると言えるほど関係が強いことを意味します。
接種数と前後X日の感染者数の相関係数をグラフにすると👇になります。

相関には「擬似相関」(ニセの相関)といって、一見相関して見えるけれども実際は関係ない場合もあります。また、これだけで因果関係が言えるわけではありません。
ただ、接種数は過去の感染者数よりも6日後の感染者数と最も相関が強いという事実から、
「感染者が増えたから接種数が増えた」という関係よりも、「接種数が増えたから感染者数が増えた」という関係が強いことがうかがわれます。
国ごとに見てみよう
以上は世界の平均の話です。
次に、各国のデータを見てみましょう。
シンガポールの場合
まずシンガポールを見てみましょう。シンガポールはすでに92%の人が2回接種を終えている世界有数の接種先進国です。(👇2回接種した人の割合)

昨年の夏以降1年間、大きな感染の波は全くありませんでしたが、この9月から感染者が激増しました。

何があったのでしょうか?
接種数のグラフと重ねて見ると、8月以前は接種数がどんなに増えても感染者数はフラットなままでした。ところが9月15日から、感染者数と接種者数はピッタリ重なって増えています。

9月以降の相関を見ると、接種数は16日後の感染者数との相関が最も強く、相関係数は『R=0.8943』です。

しかし波の始まりを見ると、感染者数の増加は7月から始まっているのに対し、接種数の波の始まりは9月半ばからです。
波の始まりは感染者数の方が先なのに、接種数は半月後の感染者数と相関が強い。これはどういうことでしょうか?
実は、シンガポールは7月から中国製〇〇チンを認めず、ファイザーかモデルナを接種するように方針を転換したのでした。
接種数のグラフは〇〇チンの種類を問わない合計値ですからグラフをみてもわかりませんが、シンガポールでは7月からファイザー・モデルナの接種が進んだと考えられます。
すると感染者数が増え始めました。それまでは(中国製の)接種数が増えても感染者数は全く増えなかったのに。
つまり、
接種数は中国製〇〇チンとは相関せず、ファイザー・モデルナと『正の相関』をしていると考えられます。
(セーシェルのように中国製〇〇チン接種開始から感染者・死者が激増している国もあり、中国国内・シンガポール用と他国用では〇〇チンが別物であることが疑われます)
だからシンガポールでは〇〇チンがファイザー・モデルナに変わってからは、世界平均と同じように、接種数が増えたら感染者数も増えたとすれば説明がつきます。
そしてシンガポールの人々がそれに気づいたのか、シンガポール政府が気づいたのはわかりませんが、10月16日をピークに〇〇チン接種数は激減し、なんと11月5日以降は接種数が報告さえされなくなってしまいました。
すると、感染者数も10月29日をピークに減少に転じたのでした。

イスラエルの場合
次に、同様に接種先進国のイスラエルを見てみましょう。
イスラエルは世界に先駆けて昨年12月から接種を開始しました。こちらは最初からほぼファイザーだけです。(余談ですが、接種を始めるのは早いイスラエルですが、接種率は今や日本よりずっと下です。危険性にいち早く気づいた人々が二の足を踏んでいるのか?はじめから上流階級は接種していないのか?抜け目ないユダヤ人の一面が垣間見えるようにも思います。)

その接種数と感染者数のグラフは、ずっとかなりきれいに連動しているように見えます。
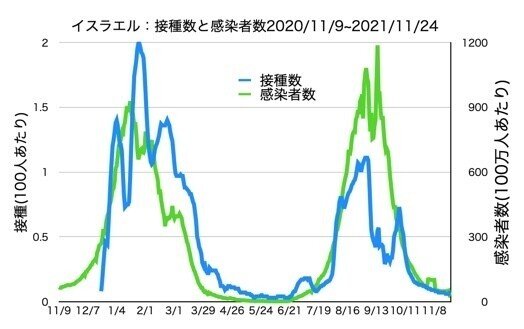
相関係数は接種数と当日の感染者数の相関係数は『R=0.7498』と相関が強いです。
特に特徴的なのは昨冬の波の3つのピークです。接種数の3つのピークに続くように、感染者数にも3つのピークができています。

接種数が何日目の感染者数と相関が強いかを調べると、イスラエルの接種開始から全期間の接種数は1日前の感染者数と最も相関が強いことがわかります。

では、イスラエルでは「感染者が増えたから接種する人が増えた」のでしょうか?
次に、イスラエルもシンガポールと同じように波ごとに区切ってみてみましょう。

まず、最近の波から見てみます。イスラエルでは今年6月後半から接種数の波が始まっています。
6月から11月の接種数と感染者数の相関を見ると、接種数は9日後の感染者数との相関が最も強く『R=0.8986』です。


ところが、昨年12月から5月までの期間では、接種数は逆に11日前の感染者数との相関が最も強く、相関係数は『R=0.9374』です。


では、今年前半までは感染者数が増えたから接種数が増え、6月からは接種数が増えたから感染者数が増えたのでしょうか?
確かに、昨年の冬にはコ○ナへの恐怖心が今より強く〇〇チンへの期待も高かったので、そうした要因はあるかもしれません。
しかしよく見ると12月から5月の波でも、感染者数のピークは接種数のピークから10日ほど遅れて起こっています。

そしてさらによく見ると、12月の感染者数の波は、接種が始まるより早く、11月からすでに立ち上がっています。

これは、波の干渉で説明できます。
新型コ○ナ感染症は〇〇チンが始まる前、昨年の初めから起こっていましたから、感染者数の波には〇〇チンによる波だけではなく、自然感染の波も含まれているのです。
11月から起こっていた自然感染による波が、12月から〇〇チン接種によって干渉されて、全体としての感染者の波は前にずれたと考えられます。
例えるなら、楽器で先にある音を鳴らしていたら、続けて別の音を鳴らした時、聞こえる音は1つの音を鳴らした時とはちがってくるようなものです。(音は波です)
あるいは、はじめに無職透明な水に青いインクを垂らした場合と、最初から少し色がついていた水に青いインクを垂らした場合では、色が変わってくるようなものです。(色・光も波です)
同じように、例えば👇このような自然感染の波と(実際はどんな形かわかりませんが)
👇この形に近い接種による感染者の波が

👇このように重なったことによって、

最終的にグラフのような感染者の波になったと考えられるのです。

『魔の2週間』が裏付けられた
以上、3回目接種以降では、接種数は、世界平均では6日後、シンガポールでは16日後、イスラエルでは9日後の感染者数と最も強く相関します。
これは、接種によって2週間ほど感染が増える時期があるという『魔の2週間』を裏付ける結果と言えます。
1〜2回目接種では、多くの西洋諸国は接種が始まった時期が自然感染の波と重なっているため、接種と感染の正の相関がわかりにくくなっています。
3回目接種では、1~2回目接種によって起こされた大きな波によって自然の波が打ち消され、津波が引いた後のように感染者数がフラットな状態になっているので接種数が感染者数を増やす関係がわかりやすくなっています。
フランスの場合
例えばフランスの接種数と感染者数はブースター接種が始まった9月から並行し、11月からはほとんどピッタリ重なっています。

👇ブースター接種数(フランス)

日本の場合
我らが日本はどうでしょうか?

日本の接種数と感染者数の相関は、イスラエルや9月以降のシンガポールほど強くありません。接種開始から11月24日までの全体で最も相関が強いのは、1~2日前の感染者数ですが、『R=0.1896』にすぎません。
グラフをパッとみても、接種数と感染者数が大きくずれている期間が多くなります。
ただ、ピークを見て見ると、接種数の最大のピークは8月10日にあり、続いて15日後に感染者のピークが来ています。
このピークのズレは、世界平均・イスラエル・シンガポールの9月以降の波と一致します。
そして、日本では9月以降、感染者の波が来ていません。
それは、まだ3回目が始まっておらず、接種数が下がり続けているからかもしれません。
3回目接種を始めた多くの国々では、それと同期するように感染者数が増加しています。
ドイツとカナダの場合
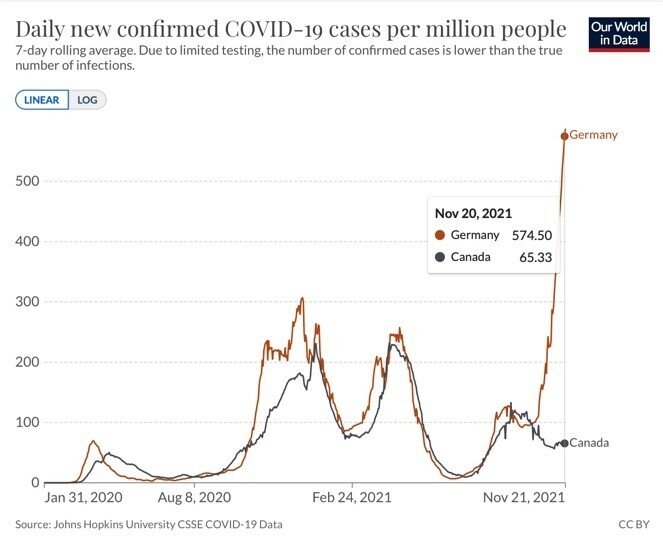
カナダとドイツは、3回目接種が始まるまでは、不思議なほど接種数も感染者数も似通っていました。

ところが、9月以降、3回目接種はドイツがカナダの3倍打ちました。


すると、ドイツの感染者数はカナダの約10倍になったのです。
ここでさらに、ドイツとカナダの接種数のグラフに、イギリスとアメリカの接種数も重ねてみます。👇

さてクイズです。
イギリスとアメリカの感染者数はどのくらいになると思いますか?
予想してみてください。
接種数はイギリスはドイツと同じくらい、アメリカはドイツとカナダの間くらいだから、感染者数もイギリスはドイツと同じくらいで、アメリカはドイツとカナダの間くらいかな?と思ったあなた!
正解です。👇

ではフランスはどのあたりでしょう?👇

接種数がアメリカとイギリス・ドイツの間くらいだから、感染者数もアメリカとイギリス・ドイツの間くらいかな?
正解です。👇

もちろんこれは、全ての国に当てはまるわけではありません。
中国の場合
例えば中国は累積接種数はアメリカより多いですが、感染者数は武漢以来ほとんど出ていません。(あまりにフラットなことを明らかにするために日本と重ねます。マスコミがあれだけ大騒ぎした武漢のアウトブレイクさえこんなにもちっぽけなものなのです)

ロシアの場合
ロシアも最近の接種数はアメリカを超えていますが、

感染者数はまだアメリカ以下です。

中国もロシアも自国独自の〇〇チンを使っています。感染者数には〇〇チンの種類などの要因も絡んでくることが伺えます。
しかしファイザー・モデルナなどの遺伝子ドクチンを中心に使っている国々では、少なくともこの9月以降の感染者数が、1~2週間前の接種数と強く正の相関をしていることは明らかでしょう。(マスクその他感染対策の影響など全く関係ないくらい)
相関係数0.9前後で6日(世界平均)~16日(シンガポール)と正相関するということは、他の要因を圧倒するほど接種数が1〜2週間後の感染者数にとって決定的な要因であるということです。
それはつまり、感染者の波が〇〇チン接種によって引き起こされていることを強く示唆するのです。
今日のテーマ曲は『フランシーヌの場合』。
『本当のことを言ったら お利口になれない...♪
本当のことを言ったら あまりにも悲しい...♪』
伝わったでしょうか?わかりにくいところおかしいところなどありましたら、ご質問・ご意見などなどぜひお寄せください^^
追記)
接種者が感染性の高いウイルスをばら撒いている事実が証明されました。
