エレガントな解法、エレファントな解法 〜モンテカルロ法を添えて〜

問 コインを100回投げて、表か裏が10回連続で出る確率は？

皆さんこの問題解けますでしょうか？私は正直解ける気がしません。そもそも何％くらいなのかすら、うまく推測できません。今日は、しかし皆さんには全然別の方法論を共有できればと思います。

その方法論とはずばり実際に投げてみましょう。「コインを100回投げて、表か裏が10回連続で出るかどうか」を100回あるいは1000回くらい試行してみたらそれなりに正しい確率が出ると思いませんか？実際にでます。

でもいくらなんでも現実にするのはつらいですよね。そこでせっかくなのでコンピュータに投げさせましょう。といっても実際に投げるのではなく、コンピュータの中で乱数（ランダム）を発生させて、それで投げていることにしましょう。プログラムで書くとこんな感じです。

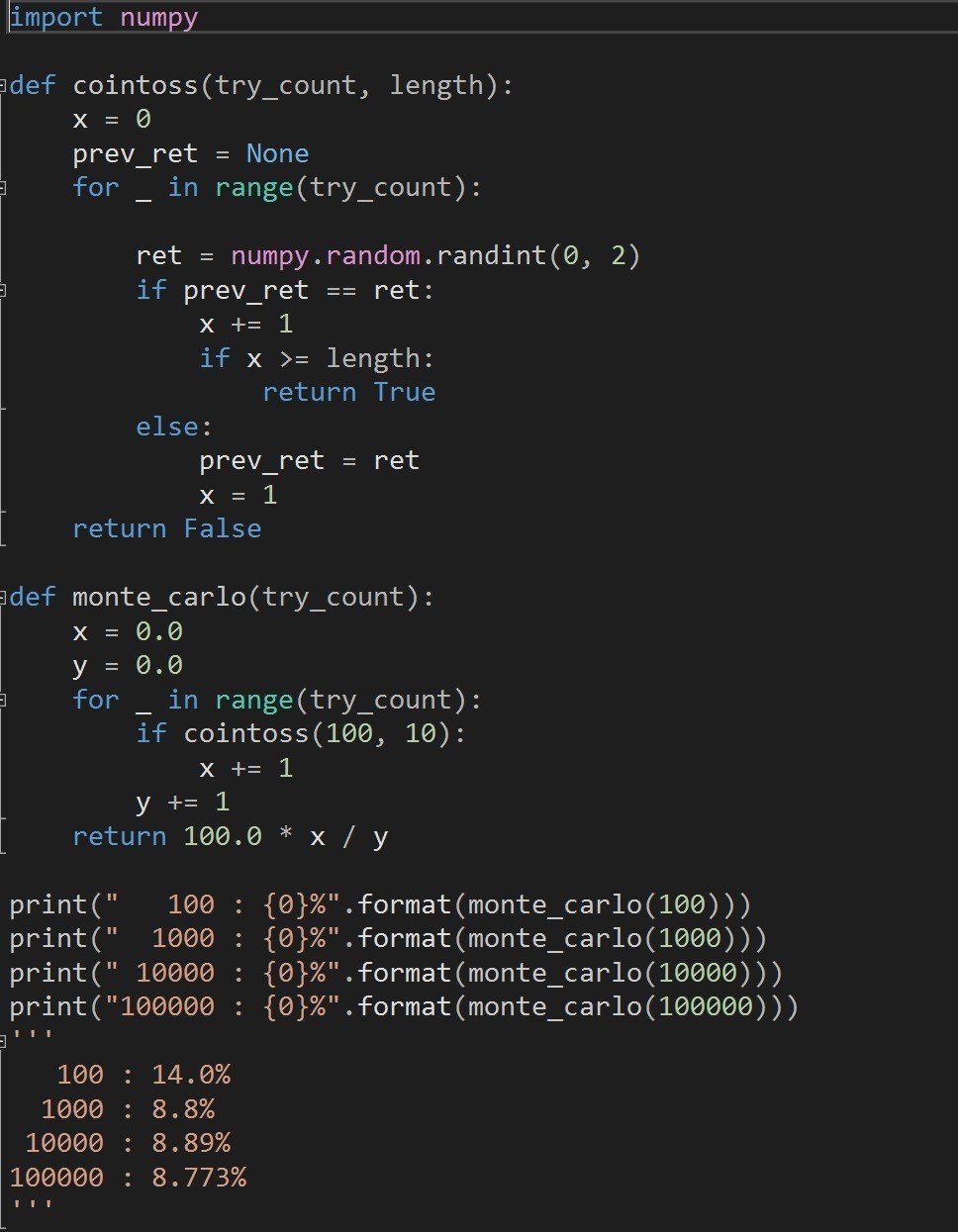
コインを100回投げて、表か裏が10回連続で出るかどうか調べるプログラム。試行回数が増えるほどに、正確な確率が出せるようになっていく。100000回程度試行させると確率は（近似解ですが）8.773％と出力される。

上のプログラムは少しプログラムに慣れてきたら15分くらいで書けるようになります。こういうコンピュータの膨大な計算能力を使って、大量にシミュレーションさせることで近似解を出す方法をモンテカルロ法といいます。多くの人にとって、”普通の数学”で解くよりもずっと簡単にできます。しかも問題に関する数学的な知識や素養がなくてもできます。ここがモンテカルロ法の素晴らしいところです。モンテカルロ法は実際にコンピュータ囲碁や複雑な積分と言った色々な分野で使われていますよ。

数学では鮮やかな解法のことを「エレガントな解法」といいます。一方、モンテカルロ法のようにコンピュータを使う力まかせの解法を「エレファントな解法」と言ったりします。ゾウのように力強い解法ということですね。

こういう方法は、あまり学校の数学では教わりません。でも現実の世界では、解決に必要な情報がすべてそろった上で問題に当たれるとは限らないので、こうしたエレファントな解法が決してかっこ悪いものではなく、もっと有効な手段として世の中に知られたらよいな、と思います。ちなみに知人の数学者さんに"エレガント"に解いていただいたら、正解は8.6659％だそうです。