2012年本試験問題 第1問 問3 送田さんと受田さんの暗号通信

辰己丈夫（放送大学）

　今回取り上げる問題，誘導に乗って解いていけば，特に難しいところはない問題です．しかし，この問題に込められた「思い」が，問題の中から聞こえてきます．そこで，その「思い」を探っていきましょう．

　いきなり，読めない名字「送田さん」「受田さん」が出てきました．名前に読みがなは付いていませんでしたので，ここは，心の目で「おくったさん」「うけたさん」と読むことにしましょう．送田さんは，受田さんに何か，秘密を伝えたい，という状況のようです．といっても，送るのはわずか1ビット．1ビットではたいした内容を送ることはできないと思う人も多いでしょうが，さぁ，どうなるでしょうか．

　秘密にして送りたいけど，秘密にできないこともあるということです．そこで対策が必要となっているのですから，これは盗み見（盗聴）されるということを指摘した選択肢を選びます．

　ですから，【タ】は⓪が正解です．

　ということで，盗聴を防ぐための工夫が導入されます．やりとりしたいデータを，どのようにして送るのか，送田さんと受田さんであらかじめ取り決めます．そのときに使われるデータが$${K}$$の値で，◆が計算方法です．

　実際にやりとりされるデータは$${C}$$です．これが$${M}$$に一致することもあれば，一致しないこともあって，それを決めているのが$${K}$$の値です．

　計算してみましょう．$${C}$$=$${M}$$◆$${K}$$= 0 ◆ 0 = 0（【チ】の正解）です．また，$${C}$$◆$${K}$$= 0 ◆ 0 = 0 ですね．無事，$${M}$$を取り出せました．

　こちらも計算してみましょう．$${C}$$=$${M}$$◆$${K}$$= 0 ◆ 1 = 1 ですから，$${C}$$◆$${K}$$= 1 ◆ 1 = 0（【ツ】の正解）ですね．無事，$${M}$$を取り出せました．

　ということで，解答群を見ましょう．

　◆の計算規則を見れば分かりますが，$${K}$$と$${C}$$の値は反転しますので，【テ】は②が正解となります．

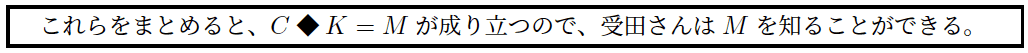
　ということで，無事に秘密の通信が終わりました．

本当に秘密かな？

　ここで，この通信を盗聴する人が登場します．

　新キャラ，見田さん登場です．多分，「みたさん」と読むのでしょう．

　計算してみましょう．$${C}$$= 0 とすると，$${M}$$= ... あれ？　$${K}$$，$${M}$$が分からないと答えられないぞ……．ということで解答群を見ます．

　なるほど．つまり，$${K}$$，$${M}$$の両方の関係を述べればいいわけです．改めて，◆の計算規則をもとに見ると，$${C}$$= 0 のときは，$${K}$$と$${M}$$の値は一致しますから，【ト】は①が正解となります．

　このようにして，見田さんは$${C}$$の値を知ることができなくなってしまいました．

複数ビットを送ろう

　冒頭から，わずか1ビットを送るために，計算方法を決め，さらに$${K}$$を決めていたわけですが，同じ方法，同じ$${K}$$の値で，もう1ビット送ってみようということになりました．

　これ，8回繰り返せば，1バイトのデータ，いわゆる半角文字を1つ送ることができます．もし，この方法を16回繰り返せば，いわゆる全角1文字を送ることができますね．

　ここは，？部分を埋めて完成させておきましょう．

表1 値の組合せ

　ということなので，表を二重線で区切り，$${M}$$と$${M′}$$が等しいところを上側に，$${M}$$と$${M′}$$が等しくないところを下側に，移動させてみました．

表1 値の組合せ（順序変更）

　そこで，解答群を見ましょう．

　二重線の上側ではつねに成立して，二重線の下側ではつねに成立しない条件を探すと，【ナ】は②が正解となります．

　でも，これは当たり前ですね．同じ計算規則と，同じ$${K}$$の値を使っているのですから，$${M}$$から$${C}$$を求める方法も固定されています．なので，$${M}$$と$${M′}$$が等しければ，$${C}$$と$${C′}$$が等しくなるのは当然です．ということで，以下の文章で問題文が終わります．

背景の解説

　ここからは，高校の情報科の範囲を，少し超えた視点も含めて，この問題の背景を説明します．

計算規則◆

　日本語では，「リンゴ，またはバナナをもらえます」というと，どちらか片方のみとなります．一方で，論理式の「AまたはB」は，「A，B の両方とも正しいときも正しい」となりますね．

　論理学には，「排他的論理和」（XOR）と呼ばれている計算規則があります．これは，「どちらか片方のみが正しいときに正しい」という規則です．先程の「リンゴ，またはバナナ」と同じです．いま，真を1で，偽を0で表すことにすると，以下の通りになります．

1$${\texttt{XOR}}$$1 = 0$${\texttt{XOR}}$$0 = 0, 1$${\texttt{XOR}}$$0 = 0$${\texttt{XOR}}$$1 = 1

　計算規則◆は，まさにこの$${\texttt{XOR}}$$そのものなのです．

情報セキュリティの3要素

　情報セキュリティを確保するということは，以下の3つの要素のすべてをバランスよく達成するように工夫することです．

• 機密性：取り扱うデータを，他人に読み取られないようにすること．

• 完全性：取り扱うデータを，破壊しないように通信・保存すること．

• 可用性：取り扱うデータを使うときに，遅滞なく利用できるようにすること．

　本文で問われているのは，送田さんと受田さんの通信内容が盗聴されないようにすることなので，機密性を達成するための通信の工夫が問われています．

暗号通信の用語との関係

　この問題，暗号通信の基本的な用語も知っておくとよいでしょう．

• 送田さんは「送信者」，受田さんは「受信者」，見田さんは「攻撃者」

• $${M}$$は平文ひらぶん（メッセージ），$${K}$$は暗号鍵（キー），$${C}$$は通信内容（コンテンツ）

　また，暗号の世界では「攻撃」というのは，平文の内容や暗号鍵が送信者と受信者以外に分かってしまうことをいいます．

この暗号を攻撃する方法

　本問の場合は，$${K}$$の値は2種類のみです．長い文章の文字コードを1ビットずつ暗号化された暗号文（ビット列）を入手できたら，それを$${K}$$= 0 と仮定して解読し，そして，$${K}$$= 1 と仮定して解読します．復号結果を見て，解釈できる方が正しい平文と言えます．

　なお，現実には，こんな簡単な暗号鍵を使うことはありません．$${K}$$の値は，たとえば256ビット程度（つまり，2$${^{256}}$$通りのどれか）になり，現実的な時間では類推はできないことになります．

　しかし，そんな大きな鍵を使っていても攻撃が可能となる場合があります．たとえば，$${M_{0}, M_{1}, · · · , M_{n}, · · · }$$を，この問題の方式で暗号化してみた場合を考えます．もし，平文が，ASCII文字コードの文章であったとしましょう．ASCII文字コードを8ビットで表記すると，最左ビットが必ず0（文字番号で，0から127まで）ですから，かならず，平文$${M_{0}, M_{1}, · · · , M_{n}, · · ·}$$には，8ビットごとに0が現れます．したがって，暗号文$${C_{0}, C_{1}, · · · , C_{n}, · · · }$$には，8ビットごとに同じビットの値が現れる，となります．

　もし，暗号文に8ビットごとに同じビットの値が現れていれば，元のデータがASCII文字コードの文章であったことが分かり，そして，それが0であったと推測することで攻撃できるのです．

ストリーム暗号・ブロック暗号

　1ビットごとに（あるいは1バイトごとに）データを暗号化する方式を，ストリーム暗号といいます．本問の暗号化は，ストリーム暗号と言えます．

　それに対して，それよりも多いデータのかたまり（ブロック）ごとに，たとえば16文字（128ビット）ごとにデータを暗号化する方式をブロック暗号といいます．

　ストリーム暗号は，データ全体を受け取らなくても暗号化・復号を行うことができるので，たとえば，動画や音声のストリーミングに用いられます．一方ブロック暗号は，処理が高速であり，データをひとまとまりにして暗号化する手順をハードウェア回路で作り出すことができるので，組込みシステムなどで利用されています．

共通鍵暗号

　本問の暗号のように，送信者と受信者が共通の鍵$${K}$$を使用する方式を，「共通鍵暗号」といいます．この方式は，事前に送信者と受信者が鍵を取り交わしておく必要があります．また，その鍵は他人に知られないように秘匿しておく必要があります．そのため，送信者と受信者のペアごとに共通鍵が必要になります．

　ところで，共通鍵暗号を採用すると，2人の場合は鍵は1種類，3人の場合は鍵は3種類，4人の場合は鍵は6種類が必要になります．この調子で増えていくと，100人の場合は4,950種類，10,000人の場合は49,995,000種類もの鍵が必要になります．鍵の種類が膨大になり，また，その鍵を事前に共有しておく必要があります．現実は，これではとても管理できないですね．では，実際にはどうなっているのでしょうか．

TLS 1.3（公開鍵暗号と共通鍵の併用）

　実は，暗号化と復号に異なる（互いに類推不可能な）鍵を用いる「公開鍵暗号」という方法があります．RSA公開鍵暗号がよく知られていますが，最近は，楕円曲線という曲線の性質を使った公開鍵暗号が普及してきました．ただし，共通鍵暗号と比べると，公開鍵暗号は計算の手間が多いので，処理に時間がかかります．

　また，通信者がそれぞれに事前に秘密の数を作成し，そこから，ある手順で作られた数を通信しあうことで共通の復号鍵を作り出す「ディフィー・ヘルマン鍵共有（DH鍵共有）」という公開鍵暗号も用いられています．やりとりされる数を盗聴しても，秘密の数や，復号鍵を推測できないようになっています．

　そして，2022年時点でのWebでの通信の多くは，これらを組み合わせたTLS 1.3 という手順（プロトコル）を採用しています．

1. 公開鍵暗号を利用した電子署名を利用して，通信相手をお互いに認証する（相手を確かめる）．

2. DH鍵共有を利用して，共有鍵を生成する（ここまでをハンドシェイクといいます）．

3. 生成した共有鍵を用いて，暗号化・通信・復号を行う．

　最後の「暗号化・通信・復号」には，AES-GCMやChaCha20といわれる方法が使われていて，ハンドシェイクよりも短い処理時間で暗号化・復号ができます．

鍵の有効期限

　先述したように，共通鍵暗号で，同じ暗号化の鍵を使い続けるのはよくありません．通常は，暗号鍵は使い捨てにします．つまり，一定回数を使用したら更新（変更）するようになっています．ブロック暗号の方法で，適当なタイミングで暗号鍵を変更することにすれば，本問にあるような攻撃はされません．

　また，通信が終わったら，その時点で共通鍵を破棄します．

（2022年6月21日受付）
（2022年7月8日note公開）

■辰己丈夫（正会員）
1991年早稲田大学理工学部数学科卒業．2014年筑波大学博士（システムズ・マネジメント）．1993年早稲田大学情報科学研究教育センター助手．その後，神戸大学．東京農工大学を経て．現在，放送大学教授．2020年6月より2年間、本会理事（新世代）．ほかに，本会広報小委員会、広聴マーケティング小委員会、教科書委員会，会誌編集委員会，初等中等教育委員会，教員免許更新講習委員会，一般情報教育委員会など各委員．

情報処理学会ジュニア会員へのお誘い

小中高校生，高専生本科～専攻科1年，大学学部１～3年生の皆さんは，情報処理学会に無料で入会できます．会員になると有料記事の閲覧，情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります．ぜひ，入会をご検討ください．入会はこちらから！