
時間短縮大作戦!
小宮常康(電気通信大学)
2013年度大学入試センター試験科目「情報関係基礎」の第3問を紹介します.プログラミングの問題です.井手先生によるnoteの記事「じゃんけんをプログラミングするよ」で触れられていた,放送大学の辰己丈夫先生が厳選した良問の1つです.
問題の冒頭の説明は次のとおりです.

利益を上げるために,利益が負の時間帯はいずれも店を閉めて,利益が正の時間帯はすべて営業するのであれば話は単純ですが,この問題では次に示す条件を満たす必要があります.

この条件のもとでは,最大総利益となる連続時間に,利益が負の時間帯が含まれることもある点に注意してください.
最後に,本問題におけるとても大切な記法【$${i, j}$$】の定義を行っています.

本問題の目標は,最大値となる【$${i, j}$$】を見つけ出すことです.
問1
まずは,【$${i, j}$$】の求め方を確認する問いです.「アイ」〜「オ」には数字が入りますが,「ア」と「ウ」には符号(-)を入れても構いません.
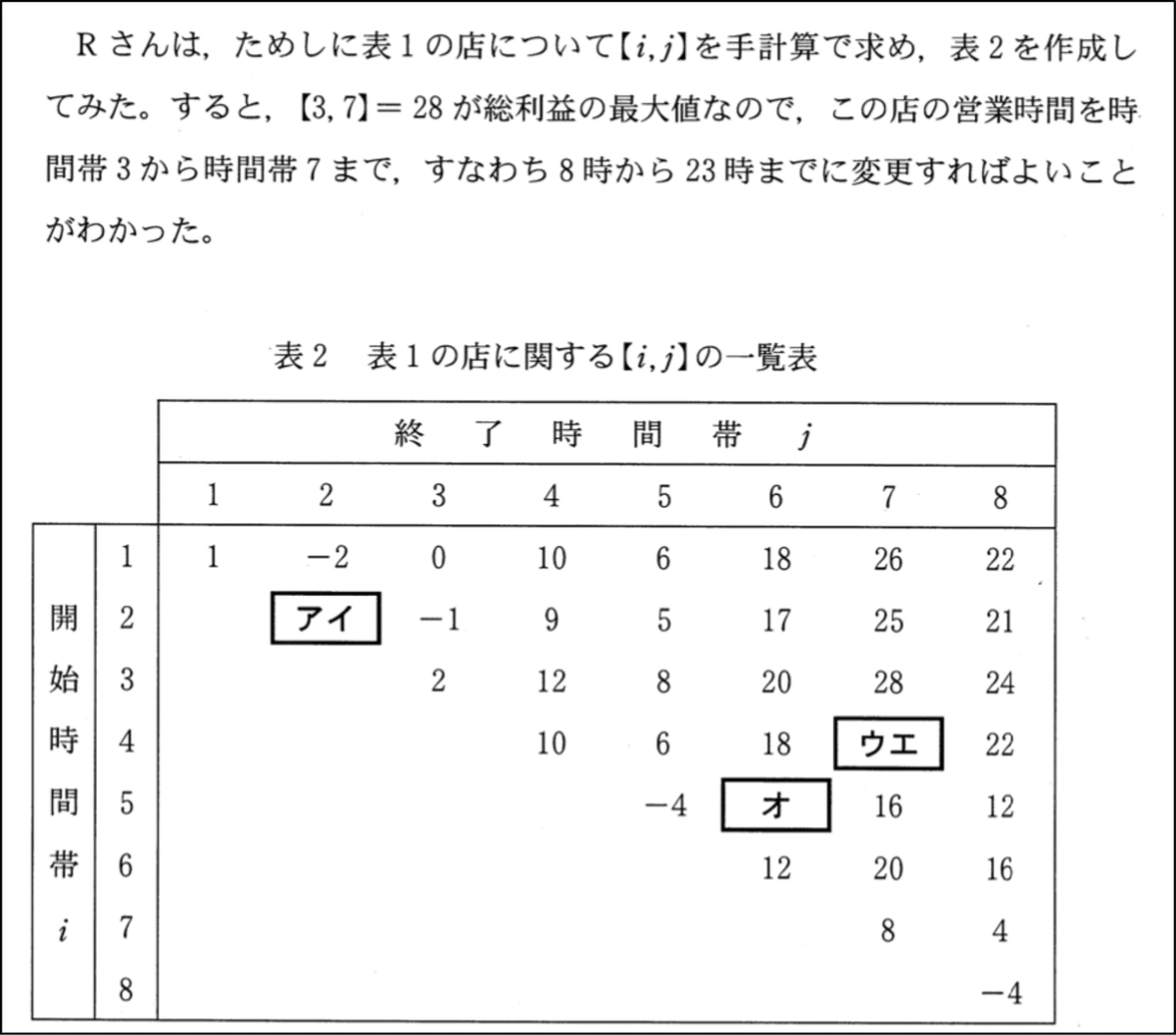
表2の見方ですが,たとえば,$${i}$$=1,$${j}$$=2のときの総利益【1, 2】が-2となっているのは,表1より,時間帯1〜2の範囲の利益の和が1+(-3)=-2だからです.
「アイ」(【2, 2】の値)の答えは,時間帯2のみの利益のことですから,表1より,時間帯2の値-3となります.
「ウエ」(【4, 7】の値)は,時間帯4〜7の連続営業による総利益であり,10+(-4)+12+8=26が答えです.【4, 7】=【4, 6】+【7, 7】=18+8=26と考えることもできます.「オ」の答えはもう分かりますね.-4+12=8です.
それでは問2にとりかかります.
問2

プログラムの全体構造を見ると,ループの中にもう1つループのある,いわゆる二重ループ構造になっています.縦横に延びる2次元の表に関する計算をするから,ということでしょう.
この二重ループでは,変数iとjの値の組み(i, j)は次のように変化します:(ク, ケ)→ (ク, ケ+1)→(ク, ケ+2)→…→(ク, 8)→(ク+1, ケ)→(ク+1, ケ+1)→…→(ク+1, 8)→…→(8, 8).変数iとjがそれぞれ開始時間帯$${i}$$と終了時間帯$${j}$$のことであるとは書かれていませんが,とりあえずそう考えて進めてみましょう.
そうすると,変数jが「ケ」から8まで一巡してから変数iが1つ増えますから,次に示すように「表2上の数値のあるところを右向きにたどり(内側のループ),行末に到達したら次の行の先頭へ移る」が外側のループで繰り返されることになります.

ちなみに変数iとjの役割を入れ替えて下に向かって計算を進めようとすると,jの値は必ず8まで動くので,空白部分の計算をしようとしてしまい不自然です.
「ク」〜「ス」の解答群は次のとおりです.

「ク」の答えは① 1ですね.「ケ」は内側のループにおけるjの初期値です.先の赤線を書き入れた表2で言うと,右向きの赤線の始まり(左端)を決める値です.表2を眺めると,$${i}$$行目の先頭要素の位置は対角線上の(i, i)であることが分かりますから,jはそのときのiの値から始めればよいので,「ケ」の答えは② iです(2013年度大学入試センター試験の問題評価・分析委員会報告書によると,正答②よりも誤答①の方が多かったとのこと).以上で,各(i, j)において【$${i, j}$$】を計算する骨格ができました.
残る空欄ですが,まずは空欄以外の部分を眺めてみましょう.soRiekiとは【$${i, j}$$】のことでしょう.この変数は繰り返しのたびに書き換えられますので,最後に求めた【$${i, j}$$】の値を保持しているはずです.
(06)〜(09)行目は,「サ」の条件が成立したら,最大総利益saidaiRiekiをその時点のsoRiekiの値で更新しています.どうやらsaidaiRiekiは暫定の最大値を記憶し,それを超える最大値が見つかり次第,新最大値へ更新されるようです.ということは,(08)行目のkaisiとsyuryoは,暫定最大総利益【$${i, j}$$】の$${i}$$と$${j}$$を暫定的に保持する変数に違いありません.つまり,「サ」「シ」「ス」の答えは,それぞれ② soRieki>saidaiRieki,② i,③ jです.
soRiekiはどう求めましょうか? (05)行目の代入のところで求めているようです.ここで繰り返しを使うわけにはいきませんから,さきほどの【4, 7】=【4, 6】+【7, 7】=【4, 6】+Rieki[7] の形で求めます. (05)行目の代入前の時点のsoRiekiには,1つ前の繰り返しで求めた【$${i, j}$$-1】の値が格納されていますから,【$${i, j}$$-1】+Rieki[j]によって【$${i, j}$$】が求まります.つまり,「コ」の答えはⓑのsoRieki+Rieki[j]です.なお,内側のループに入った直後のsoRiekiの値は(03)行目により0ですが,そのときに求める【$${i, j}$$】は表2の対角線上の値のことですからやはりこれで合っています.
最後になりましたが「カキ」について考えます.【$${i, j}$$】が求まるたびに暫定最大値と比較しますので【$${i, j}$$】の個数だけ比較します.よって,「カキ」の答えは8+7+6+…+2+1=36です.
問3

数学的な表現で手強そうですが,後ほど,この性質をもとに手続きを改良しますので,しっかりと理解しておく必要があります.問3冒頭のRさんの観察を例に,ここで述べていることを表2の上で確認してみましょう.

ここでは【$${i, k}$$】=【$${i, j}$$】+【$${j}$$+1,$${ k}$$】を○=□+△と表すことにして,表中の【$${i, j}$$】を1つ選んで□で囲み,【$${i, j}$$】がその値のときにその式を満たす【$${i, k}$$】と【$${j}$$+1, $${k}$$】すべてをそれぞれ○と△で囲ってみました.□と○の位置関係は,$${i}$$が共通で$${j}$$<$${k}$$ですから,□の後方(右側)のすべての値が○で囲まれることになります.△で囲まれる値は,$${j}$$<$${k}$$より,$${j}$$+1行目の値すべてです.ちなみに△が位置する行は,□(【$${i, j}$$】)の置かれる列の最下端の値(【$${j, j}$$】の位置)が置かれる行の次の行です.
さて,上の(1)と(2)で言っていることは,□の値に応じて,○の並びか△の並びの一方は計算不要であることが確実ということです.
【$${i, j}$$】の値(□)が負のケースでは,続く【$${i, k}$$】(○)はその負の総利益を含んだ値となっています.それに対して【$${j}$$+1, $${k}$$】(△)の方は,○で示す値から□の値を除いた値になっていますから,明らかに○より(それに対応する)△の方が(□の値だけ)大きい値になります.このケースでは,○の方はすべて計算不要です(時間帯$${i}$$〜$${j}$$は営業時間に含めない).
一方,□の値が正のケースでは,逆に○の値の方が大きく,□の値を含まない△の値はどれも計算不要というわけです.
では問3の解答にとりかかりましょう.


解答群に現れる総利益は【1, 2】【1, 4】【3, 6】【6, 7】の4つですが.実はさきほどの○□△を書き入れた表2に答えが示されています.バツ印の下に記される【1, 4】と【6, 7】は計算不要です.したがって,それらを含んだ④【1, 4】, 【6, 7】が「セ」の答えです(この設問も低正答率だったようです).
次に,この性質を活用するように手続きを改良します.まず計算の進め方の戦略です.

要は,改良版では,□の値に応じて○か△のどちらか一方へ計算を進めます.計算不要であることが確実である,選択されなかった方の並びは,この戦略により,実際に計算を省けます.なお,表2の【1, 1】から右に向かって計算を始めるところは変わっていません.
文中の「終了時間帯を次にずらして...」は,jに1を加えて引き続き○の方の計算を行うということです(このとき△の並びの計算が省略されるかどうかについては後述).「総利益が負になった場合には,そのときの終了時間帯の次を開始時間帯に設定して...」は,その時点のjに1を加えたj+1の値をiの値とするということです(i←j+1を実行).これは○の並びの計算はこれ以上進めずに△の並びへ進むことを意味します.
ところで(1)の「【$${j}$$+1, $${k}$$】(△)は計算不要」に対応する処理はどこで行われているのでしょうか? 総利益が0以上のため,【$${i, j}$$】から【$${i, j}$$+1】の計算へ進んだ(○の計算へ進んだ)瞬間,【$${j}$$+1, $${k}$$】の計算(△の並びの計算= $${j}$$+1行目の計算)の機会は失われています.たとえば,【2, 2】から【2, 3】へ進んだとします.その後,どこかの時点で「i←j+1」を実行して計算する行を変更すると,j≧3のときに「i←j+1」を実行するわけですからi≧4となり,もはや3行目に移ることはありません(もし【2, 5】まで進んで【2, 5】<0だった場合,6行目に移りますので3〜5行目はスキップされます).
改良版による計算の軌跡を表2上に示すと次のようになります.

問2のときの軌跡と比べてみてください.ずっと少ない計算で完了しています.3行目の計算では,総利益が負にならなかったので$${j}$$=8までたどり着いて計算完了です.
二重ループ構造のときと違って改良版では,jの値が1, 2, …, 7, 8と一巡したら終わりであることに注意してください.表3の終了時間帯の欄を見てもそうなっていることが読みとれます.上に示す軌跡と表3は実質同じことを表していますから,「ソ」の答えは3,「ツテ」の答えは12,「タチ」の答えは20と分かります.
いよいよ改良版手続きの作成です.

「ト」の答えはもう分かりますね.8です.問3の冒頭でつまずいたら,図2を先に見て,一重のループの構造で,jは1から8まで順に変化することを知った上で問3冒頭の説明を理解するのでも構わないと思います.
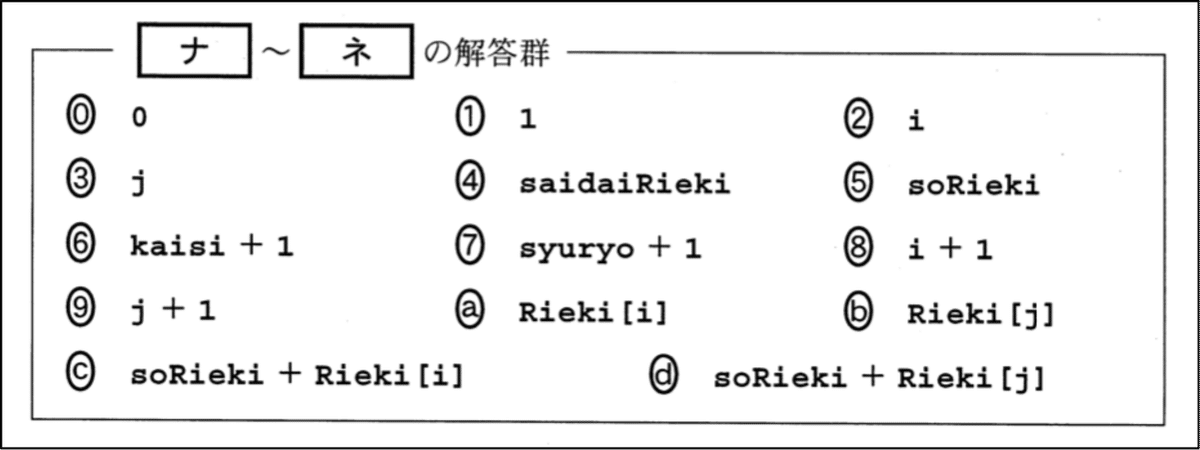
「ナ」の答えはⓓのsoRieki+Rieki[j],「ニ」の答えは② iです(改良前と同じ).「ヌ」「ネ」のある(08)行目は△の並びへ移る処理を行っています.その場合,soRiekiの計算はそれまでの累積を捨ててゼロにするのでsoRiekiを初期化する必要があります.よって「ヌ」は⓪ 0が答えとなります.「ネ」は,上で述べたとおり⑨ j+1が答えです.
手順の改良により,$${n(n}$$+1)/2回の繰り返しが$${n}$$回で済むようになりました.$${n}$$の違いで繰り返し回数が具体的にどれくらい違うか表にしてみました.

実行時間に対する繰り返し回数の影響はどれくらいだと思いますか? たとえ繰り返し1回あたりの処理時間は手続き1の方が速かったとしても,$${n}$$がとても大きくなればその影響はずっと小さくなって,繰り返し回数が大きく影響するようになることは想像できると思います.
そこで,実際に手元のコンピュータ上で実行して,どれくらいの差となるか試してみました(C言語を使用).項目数が8個しかない表1の場合,一瞬で計算は終わりますので,この計算を多数繰り返すようにして計測したところ4倍弱くらいの差でした. 10$${^{5}}$$個の項目数では(もはや営業時間見直しの目的から逸脱する項目数ですが)2.64秒 vs. 0.000138秒 (約19,000倍の差),10$${^{6}}$$個の項目数では288.01秒 vs. 0.000888秒 (約320,000倍の差)でした.両者のループ本体の処理内容が異なるなどの理由により,上の表に示す比と数値は異なりますが,比の変化具合の程度はよく似ていることが分かります.さらに項目数が10$${^{9}}$$になれば,9年 vs. 1秒くらいになりそうです!
(2022年7月25日受付)
(2022年8月12日note公開)
■小宮常康(正会員)
電気通信大学大学院准教授.プログラミング言語と言語処理系に興味を持つ.
情報処理学会ジュニア会員へのお誘い
小中高校生,高専生本科~専攻科1年,大学学部1~3年生の皆さんは,情報処理学会に無料で入会できます.会員になると有料記事の閲覧,情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります.ぜひ,入会をご検討ください.入会はこちらから!
