電磁気の考え方をコンパクトに　～コンデンサの静電エネルギー～

コンデンサの基本的な概念を確認したところで登場するのがやはりエネルギーの概念。ここではコンデンサの静電エネルギーについて考えるが、考え方はいつもと変わらない。

コンデンサの静電エネルギーは、極板に電荷が蓄えられることで生じるものであり、やはりクーロン力が為す仕事の総和として考える。初め極板に蓄えられた電気量が0であれば電場が存在しないので当然静電エネルギーは0となる。そこから徐々に極板に電荷を蓄えていくことを考えるのだが、電荷を下側極板から上側極板に移動させると電荷の偏りが生じ、極板間には電場が生じる。電場の存在下では電荷はクーロン力を受けるので、電荷の移動はクーロン力に抗って仕事を為すことで実行されることがわかる。そのときに為す仕事を足し合わせることで静電エネルギーが求まるというわけだ。それでは具体的に考えていこう。

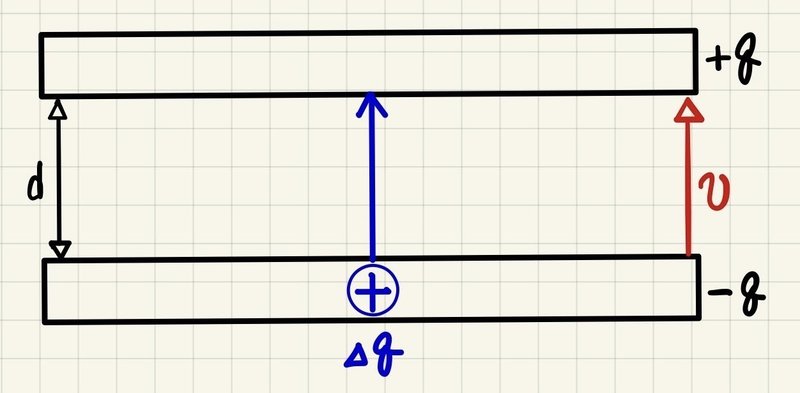
上図のようなコンデンサを考える。二枚の極板が平行に並んでおり、それぞれ+q,-qの電荷が蓄えられている。いつも通り、まずは微小仕事を考えるところから始めよう。

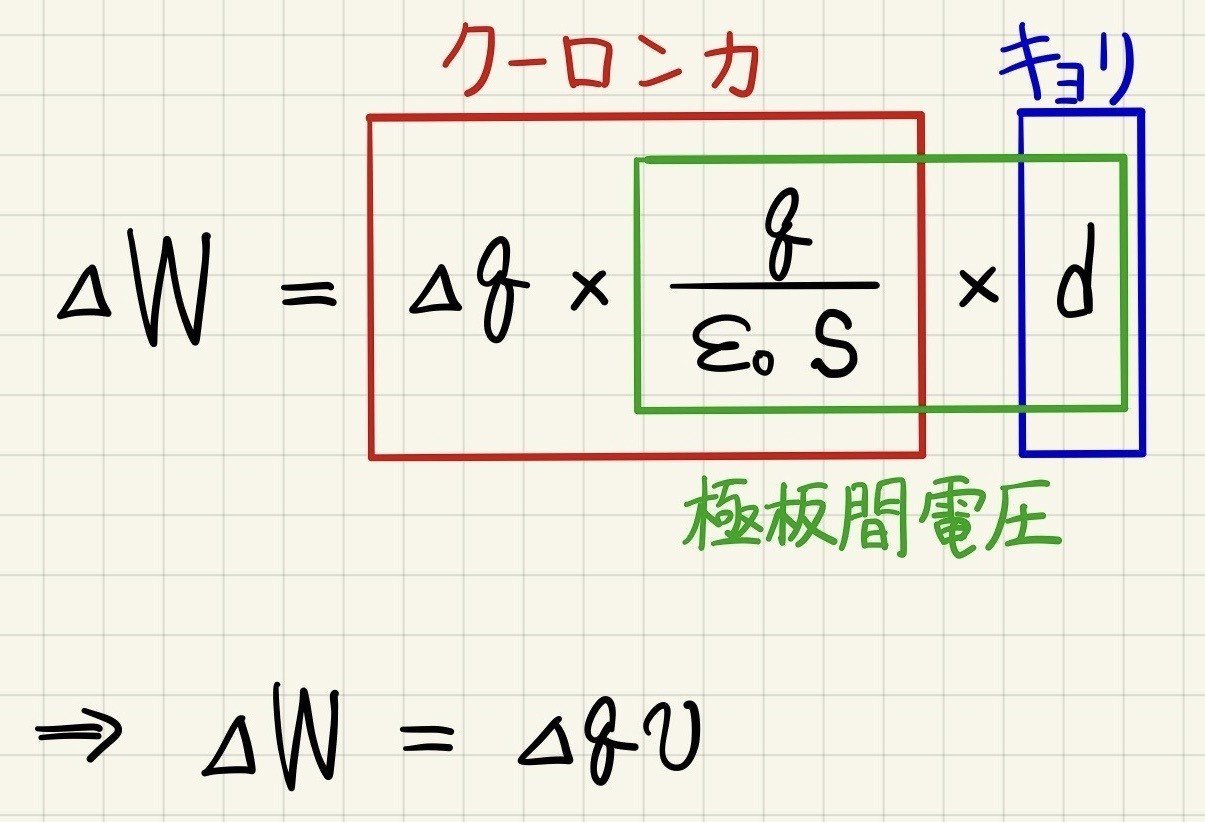
微小な電気量の電荷に対してクーロン力が極板間隔の長さ分だけ働くときに為す仕事を考える。微小な電気量の電荷が移動するとき、ΔWはクーロン力Δq×Eと極板間隔dの積で表すことができ、式の見方を少し変えることで、ΔWが微小電気量Δqと極板間電圧vの積で表せることがわかるだろう。

微小仕事を簡単な式で表すことができたところで、その累積を考える。

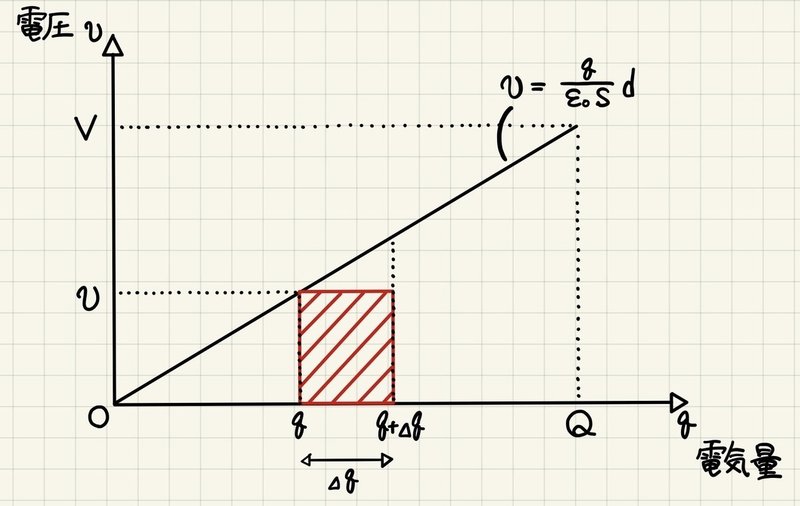
極板間電圧はqの一次式で書き表せるので、縦軸に電圧、横軸に電気量をとったグラフは直線となる。微小仕事ΔWは上図の赤斜線部なので、それを区分求積的な考え方で累積をとることにより仕事が求まる。グラフが直線であることから仕事は三角形の面積として容易に求めることができ、以下のようになる。

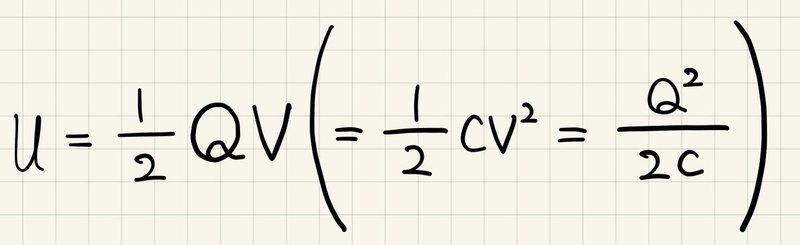
電気容量定義の式（「電磁気の考え方をコンパクトに　～コンデンサ～」を参照）を用いることで、様々な形で静電エネルギーを書き表すことができるが、この変形は瞬間的にできるものなので覚える必要はない。

クーロン力による静電エネルギーから電位を考えたとき（「電磁気の考え方をコンパクトに　～電位～」を参照）は積分を用いたので、今回も求め方だけ紹介しておく。

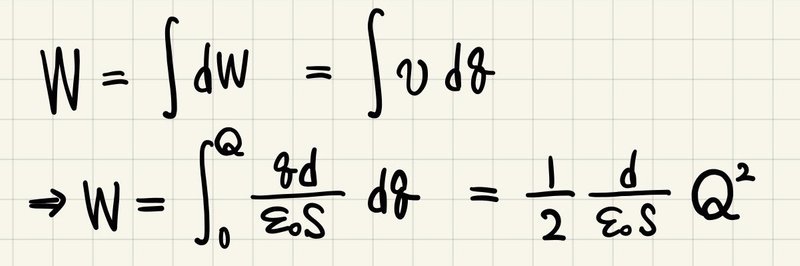
しかしここでは三角形の面積として求めたほうが簡単であるので詳しく説明はしない。（というか、区分求積的な考え方で三角形の面積として求められることを認めたところで積分を実行していると考えられる。）

今回はコンデンサの静電エネルギーを考えてみた。考え方は重力による位置エネルギーや電位の考え方と同じなので難しくはないだろう。グラフを用いた求め方と積分による求め方を自由に行き来できれば物理における積分の考え方のファーストステップはクリアしたと言えるだろう。